Operation on Numbers - Multiplication and Division
Category : 4th Class
Operation on Numbers - Multiplication and Division
Introduction
In this chapter we will study two important arithmetic operations "multiplication and division". Multiplication is repeated addition of a specific quantity, whereas division is a distribution of a quantity into some equal parts. Let us study them.
Multiplication
When a quantity is added to itself for a number of times, we use operation of multiplication to find the resulting quantity,
Find correct option for \[\mathbf{7}.\mathbf{5}\text{ }\mathbf{kg}+\mathbf{7}.\mathbf{5}\text{ }\mathbf{kg}+\mathbf{7}.\mathbf{5}\text{ }\mathbf{kg}+\mathbf{7}.\mathbf{5}\text{ }\mathbf{kg}+\mathbf{7}.\mathbf{5}\text{ }\mathbf{kg}+\mathbf{7}.\mathbf{5}\text{ }\mathbf{kg}+\mathbf{7}.\mathbf{5}\text{ }\mathbf{kg}.\]
(a) \[7\times 7.5\text{ }kg\] (b) \[9\times 7.5\text{ }kg\]
(c) \[11\times 7.5\text{ }kg\] (d) \[13\times 7.5\text{ }kg\]
(e) None of these
Answer (a)
Explanation:
\[7.5\text{ }kg+7.5\text{ }kg+7.5\text{ }kg+7.5\text{ }kg+7.5\text{ }kg+7.5\text{ }kg+7.5\text{ }kg\]\[=7\times 7.5\text{ }kg\]
Ø Example
There are 7546 books and each of the books contains 245 pages. Find the total number of pages.
Solution:
Total number of pages \[=7546\times 245\]
\[=1848770\]
Terms Related to Multiplication
(i) Multiplicand: In the multiplication, the number which is multiplied is known as multiplicand.
(ii) Multiplier: The number by which the multiplicand is multiplied is known as Multiplier.
(iii) Product: The answer or the result of multiplication is known as Product.
Look at the example given below:

Multiplication of a Number by Power of 10
When a number is multiplied by power of 10, the number of 0 is added to the right to the number, as the number of zeroes in the power of 10.
Multiply 89456 by 1000
Solution:
\[89456\times 1\underline{000}=89456\underline{000}\]
Multiplication of Two Natural Numbers
Place the multiplicands and multipliers in columns. Then multiply both the numbers of multiplicands with the first number of the multiplier from right. Now do the multiplication by second number of the multiplier and write the product in the next line in column, leaving the first place from the left, as shown below. Now add both the products, the result is your answer.
Look at the example below:
Find the product of 24 and 15
\[\mathbf{24}\times \mathbf{15}=\mathbf{360}\]
Solution:
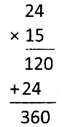
Word Problems Based on multiplication
An aeroplane is flying with the speed 1072 km/h. how much distance will It cover in 720 minutes?
Solution:
720 minutes \[=\frac{720}{60}h=12h\]
Distance covered by the aeroplane \[=1072\times 12=12864\,km.\]
Note:
The product of two natural numbers is always a natural number
Division
Division is the distribution of a quantity into some equal parts in such a way that each part contains equal amount.
Distribute 433035 kg wheat into 45 equal, parts. Find the amount of wheat each part contains,
Solution:
Amount of wheat contained in each part \[=\frac{433035}{45}kg=9623kg.\]
If 264 apples are distributed among 24 peoples, find the number of everyone will get,
Solution:
Number of apples each people will get \[=\frac{264}{24}=11\]
Terms Related to Division
(i) Dividend: The quantity that is to be divided is called dividend.
(ii) Divisor: Number of parts in which the quantity to be divided is called Divisor.
(iii) Quotient: The amount that each group gets is termed as Quotient.
(iv) Remainder: The extra amount which is left after equally distribution is called reminder.
Relation between the terms of division.
\[Dividend=Divisor\times Quotient+Remainder\]
Divide 213157 by 25 and verify the relation.
Solution:

\[\mathbf{Dividend}=\mathbf{Divisor}\times \mathbf{Quotient}+\mathbf{Remainder}\]
Dividend - 213157, Divisor = 25, Quotient = 8526, Remainder = 7
Thus \[213157=25\times 8526+7\]
Or \[213157=213150+7\]
Or \[213157=213157.\]
Word Problem Based on Division
A train cover, 7308 km, in 58 hours. Find the distance covered by .the train In 4 hours.
Solution:
Distance covered by the train in 1 hour \[=\frac{7308}{58}km\]
Distance covered by the train in 4 hours \[=126km\times 4=504km,\]
Factors of a Number
All the numbers, which divide a certain number exactly, without leaving a remainder are called factors of that number
For example: ![]()
![]() \[=1\Rightarrow 1,2,3,4,6\] and 12 are factors of 12.
\[=1\Rightarrow 1,2,3,4,6\] and 12 are factors of 12.
Note: Factors of a number always include 1 and the number it self
Find the factors of 15,
Solution: The factors of 15 are
![]()
\[\Rightarrow 1,3,5\]and 15 are factors of 15.
Which among the following is not a factor of 10?
(a) 2 (b) 5
(c) 10 (d) 3
(e) None of these
Answer (d)
Explanation: Clearly \[10\div 1=10,10\div 2=5,10\div 5=2\] and \[10\div 10=1\]
\[\Rightarrow 1,2,5\]and 10 are factors of 10.
Properties of factors:
(i) 1 is a factor of every number.
(ii) Every non-zero number is a factor of itself.
(iii) Every non-zero number is a factor of zero.
(iv) Division by 0 is meaningless.
(v) The factor of a non-zero number is either less than or equal to the number.
Which among the following statements is not true?
(a) 2 is not a factor of 2. (b) 26 is a factor of 0.
(c) 28 is not a factor of 4. (d) 4 is not a factor of 28.
(e) None of these
Answer (d)
Explanation: Every number is a factor of itself so 2 is a factor of 2.
Every non-zero number is a factor of 0. So 26 is a factor of 0.
The factor of a non-zero number cannot be greater than the number
So, 28 can't be a factor of 4.
\[\therefore ~28=1\times 2\times 2\times 7\]
\[\Rightarrow 1,2,4,7,14\]and 28 are factors of 28.
Even and Odd Numbers
Even numbers: A number is called an even number if 2 is a factor of the number. In other words, A number, which is a multiple of 2 is called an even number
For example: 0, 2, 4, 6, 8, 10, 12, 14, 16 are even numbers.
Odd numbers: A number, which is not a multiple of 2 is called an odd number.
For example \[1,3,5,7,9,11,.........\] are odd numbers.
Which one among the following is not an even number?
(a) 0 (b) 89990
(c) 1049 (d) 2032
(e) None of these
Answer (c)
Explanation: 1049 is not a multiple of 2 and so is not an even number.
Prime Factors
Factors of a number written in primes are called prime factors of that number.
For example: \[24=2\times 2\times 2\times 3\]
\[\Rightarrow \]prime factors of 24 are \[2\times 2\times 2\times 3\]
Multiples
You already know that multiples of 2 are\[2,4,6,8,10,12,14,16,18,20,....\]. So all the numbers that comes in the table of 2 are its multiples. Multiples are never ending.
So it is not possible to find the last multiple of any number
Write first five multiples of 8 and 16 and find common multiples of
Solution: First five multiples of \[8=8,16,24,32,40\]
First five multiples of \[16=16,32,48,64,80\]
Clearly common multiples from first five multiples of 8 and 16 are 16 and 32.
Which one among the following is not a multiple of 11?
(a) 101 (b) 121
(c) 154 (d) 176
(e) None of these
Answer (a)
Explanation: Clearly, \[121=11\times 11,\,154=11\times 14\]
\[176=11\times 16\text{ }and\text{ }101=1\times 101\]
Here 101 is a prime number and it is not a multiple of 11.
Properties of Multiples
(i) Every number is a multiple of 1.
(ii) Every non-zero number is a multiple of itself.
(iii) Multiples of any number are infinite,
(iv) Every non-zero multiple of a non-zero number is either greater than or equal to the number.
Highest Common Factor
The highest common factor among two or more given numbers is called the highest common factor or (H.C.F.).
Find the HCF of 12 and 16.
Solution: \[\therefore 12=2\times 2\times 3\]and \[16=2\times 2\times 2\times 2\]
\[\therefore HCF\] of 12 and \[16=2\times 2=4\]
Alternet Method
Factors of \[12=1,2,4,6,12\left\{ \therefore 12=1\times 2\times 2\times 3 \right\}\] and
Factors of \[16=1,2,4,8,16\left\{ \therefore 16=1\times 2\times 2\times 2\times 2 \right\}\]
\[\therefore \]Highest common factors of 12 and
Lowest Common Multiple (L.C.M.)
Since multiples of a number are uncountable. So it is not possible to get the highest common multiple. Let us learn the steps used to find the lowest common multiple of two numbers.
Step 1: Find first few multiples of smaller number.
Step 2: Find first few multiples of larger number till we get a common multiple of both the numbers.
Step 3: The common multiple so obtained will be the lowest common multiple of both the numbers.
Find the lowest common multiple of 4 and 10.
Solution:
Step 1: First 6 multiples of 4 are \[4,8,12,16,20,24\]
Step 2: First 2 multiples of 10 are 10, 20
Step 3: Clearly 20 is the first common multiple of both the numbers.
So, 20 is the LCM of 4 and 10.
Alternate Method
First write both the numbers separated with a comma, and then find the prime factors of both the number as shown below.
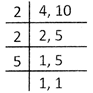
So LCM of 4 and 10 is \[2\times 2\times 5=20\]
You need to login to perform this action.
You will be redirected in
3 sec
