Algebra
Category : 4th Class
Algebra
Learning Objectives
Fraction
Fraction represents a part of whole or any number of equal parts. A line separates the two terms. Number above the line is called numerator and the number below the line is called denominator. Denominator of a fraction tells us how many parts the whole is divided into and the numerator tells us how many parts are taken out the whole. Let 4 kg of flour is divided into five equal parts. The amount of each part is represented as \[\frac{4}{5}\] kg. Here, the number four-fifth is known as fractional number and its symbol \[\frac{4}{5}\] is called fraction.
Understanding Fractions
Fractions are formed when we have a whole that is divided into so many equal parts. The shaded portion of a figure can also be represented by a fraction as shown in the table given below.
|
Shaded Part |
Fraction |
Fractional Number |
Figure |
|
1 part out of 6 equal parts
|
\[\frac{1}{4}\] |
One-fourth |
|
|
3 part out of 6 equal parts
|
\[\frac{3}{6}\] |
Three-sixth |
|
|
5 part out of 8 equal parts
|
\[\frac{5}{8}\] |
Five-eighth |
|
|
2 part out of 6 equal parts
|
\[\frac{2}{6}\] |
Two-sixth |
|
|
4 parts out of 7 equal parts
|
\[\frac{4}{7}\] |
Four-seventh |
|
|
5 part out of 6 equal parts
|
\[\frac{5}{6}\] |
Five-sixth |
|
Types of Fractions
There are several types of fractions. Let us study the fractions and their types.
Proper and Improper Fractions
A proper fraction is one whose numerator is smaller than the denominator. For example, \[\frac{3}{4},\frac{17}{21},\frac{27}{29}\] are proper fractions. An improper fraction is one whose numerator is bigger than the denominator. For example, \[\frac{5}{4},\frac{8}{5},\frac{23}{21}\] are improper fractions.
Mixed Fractions
A mixed fraction is the ratio of a whole number and a fraction combined into one mixed number.
For example, \[1\frac{3}{4},2\frac{7}{9},3\frac{4}{5}\] are mixed fractions.
Equivalent Fractions
Fractions which have the same value though they may look different are called equivalent fractions. For example, \[\frac{1}{3},\frac{2}{6},\frac{3}{9},\frac{4}{12}\] are equivalent fractions because all are one-third.
Decimals
A decimal or decimal number is a fraction written in special form. A decimal is a fraction which has 10, 100, 1000, etc. for its denominator and it is expressed in the decimal system of notation. For example, \[\frac{9}{10}\] and \[1\frac{9}{100}\] can be written in decimal form as 0.9 and 1.09, respectively. A decimal number is broadly divided into two parts: Whole number part and Decimal part. The two parts are separated by a dot (.) called the decimal point. From the decimal point, as we move on the left, the place value is multiplied by 10 and as we move on the right, it is divided by 10.
|
Decimal Fraction |
Whole Part |
Decimal Part |
|
5.3 |
5 |
3 |
|
147.81 |
147 |
81 |
|
15.679 |
15 |
679 |
|
0.8 |
0 |
8 |
|
1.004 |
1 |
004 |
Decimal Place Value Chart
The following chart shows the value of each place in a decimal number.
|
Hundreds |
Tens |
Ones |
Decimal Point |
Tenths |
Hundredths |
Thousandths |
Ten Thousandths |
|
100 |
10 |
1 |
. |
\[\frac{1}{10}\] |
\[\frac{1}{100}\] |
\[\frac{1}{1000}\] |
\[\frac{1}{10000}\] |
Here, the values of left of the decimal point are whole numbers and numbers written after the decimal point or right of the decimal point is always less than one. Putting a zero before the decimal point indicates that there are no whole numbers.
What is Unitary Method?
The term ‘unitary method’ is a technique which has evolved from the concept of 'unit' which means one. Therefore, the unitary method is also known as the method of ones.
In unitary method:
Example:
1. If the price of one bicycle is Rs.1200, then what is the price of such 5 bicycles?
Solution: Here, price of 1 bicycle is given and we have to find the price of 5 such bicycles. Therefore, we multiply the price of 1 bicycle by 5.
Hence, price of 5 bicycles = Rs. (\[1200\times 5\]) = Rs.6000
2. If the price of 8 bicycles is Rs. 10200, then what is the price of 1 such bicycle?
Solution: Here, price of 8 bicycles is given and we have to find the price of 1 such bicycle. Therefore, we divide the price of 8 bicycles by 8.
Hence, price of 1 bicycle = Rs. (\[10200-8\]) = Rs.1275
Rules Applied in Unitary Method
Rule 1: If we know the value of one then to find the value of many, we do multiplication.
Example:
1. If the cost of 1 chair is Rs. 345, then find the cost of 7 such chairs.
Solution: Given that the cost of 1 chair = Rs. 345
Therefore, the cost of 7 chairs = Rs. (\[345\times 7\]) = Rs.2415
Rule 2: If we know the value of many then to find the value of one, we do division.
2. If the cost of 8 pencils is Rs. 68, then find the cost of 1 such pencil.
Solution: Given that the cost of 8 pencils = Rs.68
Therefore, the cost of 1 pencil = Rs. (\[68\div 8\]) = Rs.8.50
Rule 3: If we know the value of many then to find the value of more than given or less than given, we first need to calculate the value of one.
3. If the cost of 4 apples is Rs. 38, then find the cost of 6 such apples.
Solution: Given that the cost of 4 apples = Rs.38
Therefore, the cost of 1 apple = Rs. (\[38\div 4\]) = Rs.9.50
So, the cost of 6 apples =Rs. (\[9.50\times 6\]) = Rs.57
4. A train is running at a uniform speed. It covers 840 km in 7 hours. How much distance will it cover in 5 hours?
Solution: Clearly, in more hours, the train will cover more distance and in less hours, the train will cover less distance.
Here, distance covered in 7 hours = 840 km
So, the distance covered in 1 hour = (\[840\div 7\]) km = 120 km
Therefore, the distance covered in 5 hours = (\[120\times 5\]) km = 600 km
Problems Based on Unitary Method
Some examples of problems based on unitary method are given below. Let us study the following examples.
Example:
1. There are 1250 toffees in a packet. How many toffees are there in 9 such packets?
Solution: Number of toffees in 1 packet = 1250
Therefore, the number of toffees in 9 packets = \[1250\times 9\] = 11250
2. If the cost of half dozen bananas is Rs. 15, then find the cost of one banana.
Solution: Given that the cost of half dozen bananas = Rs.15
Or, the cost of 6 bananas = Rs.15
Therefore, the cost of 1 banana = T (\[15-6\]) = Rs.2.50
3. If 8 litres of petrol is consumed by a car in covering a distance of 324 km, then how many kilometres will it cover in 10 litres of petrol?
Solution: In 8 litres of petrol, car covered the distance = 324 km
Therefore, in 1 litre of petrol, the car covered the distance
= (\[324\div 8\]) km = 40.5 km
So, in 10 litres of petrol, the car will cover the distance
= (\[40.5\times 10\]) km = 405 km
Commonly Asked Question
1. Which one of the following is a pair of like fractions?
(a) \[\frac{3}{17},\frac{17}{3}\]
(b) \[\frac{12}{18},\frac{16}{10}\]
(c) \[\frac{4}{17},\frac{14}{17}\]
(d) \[\frac{14}{21},\frac{14}{22}\]
(e) None of these
Answer (c) is correct.
Explanation: Fractions in which the denominators are the same, are called like fractions. Therefore, \[\frac{4}{17},\frac{14}{17}\] are like fractions.
2. In the decimal number 24.9785, what is the place value of 8?
(a) Tenths (b) Hundredths
(c) Thousandths (d) Ten thousandths
(e) None of these
Answer (c) is correct.
Explanation: Here, 8 is at third place right from the decimal point.
Therefore, it is at \[\frac{1}{1000}\] place in place value chart.
So, the place value of 8 is thousandths.
3. In which one of the following figures, the fraction represented by shaded parts is equal to\[\frac{1}{3}\] ?
(a)  (b)
(b) 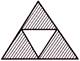
(c) ![]() (d)
(d) 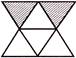
(e) None of these
Answer (d) is correct.
Explanation: Here, we have:
In option (a); fraction represented by the shaded parts = \[\frac{3}{5}\]
In option (b); fraction represented by the shaded parts = \[\frac{3}{4}\]
In option (c); fraction represented by the shaded parts = \[\frac{2}{7}\]
In option (d); fraction represented by the shaded parts = \[\frac{2}{6}\] = \[\frac{1}{3}\]
Therefore, the required figure is given in option (d).
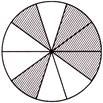
4. The fraction represented by shaded parts in the figure given below is equal to:
(a) 0.2 (b) 0.4
(c) 0.5 (d) 0.6
(e) None of these
Answer (c) is correct.
Explanation: Number of shaded parts = 5
Total number of parts = 10
Fraction represented by shaded parts = \[\frac{5}{10}\]
Therefore, the required decimal number = \[5\div 10\] = 0.5
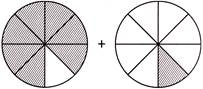
5. Which one of the following represents the sum of fractions represented by shaded parts in the figures shown below?
(a) \[\frac{7}{8}+\frac{7}{8}\]
(b) \[\frac{7}{8}+\frac{1}{8}\]
(c) \[\frac{1}{8}+\frac{1}{8}\]
(d) \[\frac{1}{8}+\frac{1}{4}\]
(e) None of these
Answer (b) is correct.
Explanation: Here, we observe that:
Fraction represented by the shaded parts in left side figure = \[\frac{7}{8}\]
and, fraction represented by the shaded parts in right side figure = \[\frac{1}{8}\]
Thus, the required sum of fractions = \[\frac{7}{8}+\frac{1}{8}\]
6. If we arrange the digits of decimal number 35.564 in the decimal place value chart, place value of 4 will be:
(a) thousands (b) tenths
(c) hundredths (d) thousandths
(e) None of these
Answer (d) is correct.
Explanation:
|
Tens |
Ones |
Decimal Point |
Tenths |
Hundredths |
Thousandths |
|
3 |
5 |
|
5 |
6 |
4 |
7. Arrange the decimals given below in descending order:
0.392, 3.092, 0.0392, 3.0092
(a) 0.0392, 0.392, 3.0092, 3.092
(b) 3.092, 0.392, 0.0392, 3.0092
(c) 3.0092, 3.092, 0.392, 0.0392
(d) 3.092, 3.0092, 0.392, 0.0392
(e) None of these
Answer (d) is correct.
Explanation: Here, we have:
\[0.392=\frac{392}{1000}=\frac{392\times 10}{1000\times 10}=\frac{3920}{10000}\]
\[3.092=\frac{3092}{1000}=\frac{3092\times 10}{1000\times 10}=\frac{30920}{10000}\]
\[0.0392=\frac{392}{10000}\] and \[3.0092=\frac{30092}{10000}\]
Clearly, 30920 > 30092 > 3920 > 392; or, 3.092 > 3.0092 > 0.392 > 0.0392
Hence, the decimals in descending order are: 3.092, 3.0092, 0.392, 0.0392
8. In the magic square given below, the sum of fractions in each row, each column and each diagonal is same. Find the sum of missing fractions P and Q.
|
\[\frac{4}{13}\] |
\[\frac{3}{13}\] |
\[\frac{8}{13}\] |
|
P |
\[\frac{5}{13}\] |
\[\frac{1}{13}\] |
|
\[\frac{2}{13}\] |
Q |
\[\frac{6}{13}\] |
(a) \[\frac{6}{13}\] (b) \[\frac{17}{13}\]
(c) \[\frac{19}{13}\] (d) \[\frac{21}{13}\]
(e) None of these
Answer (a) is correct.
Explanation: Here,
Sum of fractions in one diagonal = \[\frac{4}{13}+\frac{5}{13}+\frac{6}{13}=\frac{4+5+6}{13}=\frac{15}{13}\]
Hence, P = \[\frac{15}{13}-\left( \frac{4}{13}+\frac{2}{13} \right)=\frac{15}{13}-\frac{6}{13}=\frac{15-6}{13}=\frac{9}{13}\]
And, Q = \[\frac{15}{13}-\left( \frac{3}{13}+\frac{5}{13} \right)=\frac{15}{13}-\frac{8}{13}=\frac{15-8}{13}=\frac{7}{13}\]
Also, numerators of all fractions are: 1, 2, 3, 4, 5, 6, 7, 8, 9 where, 7 and 9 are missing. So, the required sum (P + Q.) = \[\frac{9}{13}+\frac{7}{13}+\frac{16}{13}\]
9. I bought \[2\frac{1}{4}\] kg of apples, \[1\frac{1}{4}\] kg of oranges and \[\frac{1}{2}\] kg of grapes. How much weight did I carry home?
(a) 16 kg (b) 8 kg
(c) 6 kg (d) 4 kg
(e) None of these
Answer (d) is correct.
Explanation: Here,
Sum of all weights = \[\left( 2\frac{1}{4}+1\frac{1}{4}+\frac{1}{2} \right)\] kg
= \[\left( \frac{2\times 4+1}{4}+\frac{1\times 4+1}{4}+\frac{1\times 2}{2\times 2} \right)\] kg
=\[\left( \frac{8+1}{4}+\frac{4+1}{4}+\frac{2}{4} \right)\] kg
= \[\left( \frac{9}{4}+\frac{5}{4}+\frac{2}{4} \right)\] kg = \[\left( \frac{9+5+2}{4} \right)\] kg
= \[\left( \frac{16}{4} \right)\] kg = \[\left( \frac{16\div 4}{4\div 4} \right)\] kg = \[\frac{4}{1}\] kg = 4 kg
10. Match the following and choose the correct option.
|
(A) |
Rs.10 |
(1) |
Five 50 paise coins |
|
(B) |
Rs.1 |
(2) |
Twenty 50 paise coins |
|
(C) |
Rs.2.50 |
(3) |
Nine 50 paise coins |
|
(D) |
Rs.4.50 |
(4) |
Two 50 paise coins |
(a) A - 4, B - 2, C - 1, D - 3
(b) A - 2, B - 3, C - 4, D - 1
(c) A - 1, B - 3, C - 2, D - 4
(d A - 2, B - 4, C - 1, D - 3
(e) None of these
Answer (d) is correct.
Explanation: (i) Rs. 10 is equal to twenty 50 paise coins.
(ii) Rs. 1 is equal to two 50 paise coins.
(iii) Rs. 2.50 is equal to five 50 paise coins.
(iv) Rs. 4.50 is equal to nine 50 paise coins.
11. Paul has thirty four 50 paise coins. How much amount in rupees does he have?
(a) Rs. 34 (b) Rs. 17
(c) Rs. 68 (d) Rs. 8.50
(e) None of these
Answer (b) is correct.
Explanation: Two 50 paise coins make Rs.1
Therefore, thirty four 50 paise coins make Rs. \[\left( \frac{34}{2} \right)\] = Rs.17
12. If the cost of 6 ball pens is Rs. 63, then the cost 2 such ball pens is:
(a) Rs.28 (b) Rs.94.50
(c) Rs.21 (d) Rs.31.50
(e) None of these
Answer (c) is correct.
Explanation: Here, the cost of 6 ball pens = Rs.63
Now, the cost of 1 ball pen = Rs. (\[63\div 6\]) = Rs.10.50
Hence, the cost of 2 ball pens = Rs. (\[10.50\times 2\]) = Rs.21
13. How many paise should be added to Rs. 2.10 to make it 385 paise?
(a) 165 paise (b) 170 paise
(c) 185 paise (d) 175 paise
(e) None of these
Answer (d) is correct.
Explanation: As we know, subtraction is the inverse process of addition.
Here, Rs. 2.10 = (\[2.10\times 100\]) paise = 210 paise
Difference of 385 paise and 210 paise = (\[385-210\]) paise = 175 paise
Hence, 175 paise should be added to Rs. 2.10 to get 385 paise.
14. If a cow gives 13 litres of milk per day, then how much milk does the cow gives in a week?
(a) 84 litres (b) 77 litres
(c) 104 litres (d) 91 litres
(e) None of these
Answer (d) is correct.
Explanation: As we know, the number of days in a week = 7
Now, in 1 day, the cow gives 13 litres of milk.
So, in 7 days, the cow will give (\[13\times 7\]) litres = 91 litres of milk.
Hence, the cow gives 91 litres of milk in a week.
15. If the cost of eight baskets of fruits is Rs.2568, then the cost of 1 basket of fruits is:
(a) Rs.321 (b) Rs.214
(c) Rs.341 (d) Rs.361
(e) None of these
Answer (a) is correct.
Explanation: Given that 8 baskets of fruits cost Rs.2568.
Therefore, 1 basket of fruits cost Rs. (\[2568\div 8\]) = Rs.321
16. A man works for 6 days and earns Rs.5118. How much does he earn in a day?
(a) Rs.848 (b) Rs.798
(c) Rs.853 (d) Rs.913
(e) None of these
Answer (c) is correct.
Explanation: Given that the man works 6 days and earn Rs.5118.
Therefore, the man works 1 day and earns Rs. (\[5118\div 6\]) = Rs.853
17. Mohit types 900 words in half an hour. How many words would he type in 6 minutes?
(a) 120 words (b) 210 words
(c) 150 words (d) 180 words
(e) None of these
Answer (d) is correct.
Explanation: Since, half an hour = 30 minutes
Now, in 30 minutes, Mohit types 900 words
So, in 1 minute, Mohit types (\[900\div 30\]) words = 30 words
Therefore, in 6 minutes, Mohit would type = (\[30\times 6\]) words = 180 words.
18. If the cost of half dozen guavas is Rs.15, then find the cost of two and half dozen guavas.
(a) Rs.120 (b) Rs.90
(c) Rs.75 (d) Rs.60
(e) None of these
Answer (c) is correct.
Explanation: Since, half dozen = 6. Now, the cost of 6 guavas = Rs.15
Therefore, the cost of 1 guava = Rs. (\[15-6\]) = Rs.2.50
Now, two and half dozen = \[12+12+6=30\]
Hence, the cost of 30 guavas = Rs. (\[2.50\times 30\]) = Rs.75
19. A local farmer sells onions in 5 kg bags at Rs.87.50 per bag and 9 kg bags at Rs.148.50 per bag. Is there any monetary advantage gained if you buy the 9 kg bag?
(a) Maybe (b) Yes
(c) No (d) Can't say
(e) None of these
Answer (b) is correct.
Explanation: Here, if you buy 5 kg bag, the cost of 1 kg of onions = Rs. (\[87.50\div 5\]) = Rs.17.50
And, if you buy 9 kg bag, the cost of 1 kg of onions = Rs. (\[148.50\div 9\]) = Rs.16.50
Hence, 9 kg bag is comparatively cheaper than that of 5 kg bag.
So, yes there is a monetary advantage gain in buying the 9 kg bag.
20. I can buy 6 burgers for Rs.90. How much money would I need if I wanted to buy 90 such burgers?
(a) Rs.1350 (b) Rs.1290
(c) Rs.1250 (d) Rs.1130
(e) None of these
Answer (a) is correct.
Explanation: Given that the cost of 6 burgers = Rs.90
Therefore, the cost of 1 burger = Rs. (\[90\div 6\]) = Rs.15
Hence, the cost of 90 burgers =Rs. (\[15\times 90\]) =Rs.135
You need to login to perform this action.
You will be redirected in
3 sec
