Applied Mathematics: Percentage, Ratio and Proportion
Category : 5th Class
Applied Mathematics: Percentage, Ratio and Proportion
Introduction
You must have heard the word percentage in day-to ?day conversation.
· Ms. Arora?s daughter has got 94% in her Board Exam.
· V-Mart is giving 50 percentage discount.
The word ?Percentage? has come from two words: Per and Cent. Per means ?out of? and cent means ?Hundred?. So the word percentage means out of hundred or per hundred. In this chapter, we will study about percentage, profit/loss, ratio and proportion, direct and inverse variations and their use in our everyday life.
Percentage
All fraction that are written with a denominator of 100 can be written as percentages. The symbol for percentage is %. Percentage can be shown using diagrams. Look at the given square below. It is divided into 100 smaller squares. The shaded squares will always be a fraction of 100. In this given figure, there are 23 shaded squares.

Since, 23 out of 100 squares are shaded, we can say \[\frac{23}{100}\] of the whole part (large square) is shaded. Here, \[\frac{23}{100}\] has 100 as its denominator, we call it a percentage. \[\frac{23}{100}\] can be named as 23 percent of 23% So, \[\frac{23}{100}\]= 23% and 23% = \[\frac{23}{100}\]. Remember that the numerator of a fraction with denominator 100 will be percentage.
Which of the following relations is correct?
(a) 0.34 = 34 % =\[\frac{17}{25}\] (b) 0.64 = 64% =\[\frac{16}{25}\]
(c) 0.19 = 19% =\[\frac{19}{10}\] (d) 1.28 = 28% =\[\frac{32}{25}\]
Explanation: In option (A): 0.34 = \[(0.34\,\,\times \,\,100)%\] = 34 = \[\frac{34}{100}\] = \[\frac{34+2}{100\div 2}\] = \[\frac{17}{50}\]
In option (B): 0.64 = \[(0.64\,\,\times \,\,100)%\]= 64 = \[\frac{64}{100}\] = \[\frac{64\div 4}{100\div 4}\] = \[\frac{16}{25}\]
In option (C): 0.19 = \[(0.19\,\,\times \,\,100)%\] = 19% = \[\frac{19}{100}\]
In option (D): 1.28 = \[(1.28\,\,\times \,\,100)%\]= 128% = \[\frac{128}{100}\] = \[\frac{128\div 4}{100\div 4}\] = \[\frac{32}{25}\]
Clearly, relation given in option (B) is correct.
Money and Metric Measure as Percentage
Observe the following:
100 paise = one rupee; so 1 paisa = \[\frac{1}{100}\] of a rupee = 1% a rupee.
100 cm = 1 meter; so 1 centimeter = \[\frac{1}{100}\] meter = 1% of a meter.
1000 grams = 1 kilogram; so 1 gram = \[\frac{1}{1000}\] kilogram
\[=\,\,\left( \frac{1}{1000}\,\times \,100 \right)%\]of a kilogram \[\frac{1}{10}%\] of a kilogram = 0.1% of a kilogram
What per cent of a rupee is 4 paise?
(a) 8% (b) 40%
(c) 4% (d) 20%
(e) None of these
Answer (c)
Explanation:
As we know, 1 paisa = 1% of a rupee. So, 4 paise = 4% of a rupee.
Also, if we suppose, x% of a rupee is 4 paise, then x% of 1 rupee = 4 paise
Or, \[\frac{x}{100}\,\,\times \,\,100\,\,=\,\,4.\]Or \[x\,\,=\,\,\frac{4\times 100}{100}%\,\,=\,\,4%.\]
Rahul earned Rs. 15500 per month. He saved 45% of his salary every month. How much did he spend every month in terms of rupees?
(a) Rs. 7550 (b) Rs. 8525
(c) Rs. 8075 (d) Rs. 8425
(e) None of these
Answer (b)
Explanation:
Amount that Rahul earned every month = Rs. 15, 500
Rahul?s saving in per cent = 45%
So, the amount that Rahul saved every month = 45% of Rs. 15500
\[=\,\,Rs.\left( \frac{45\times 15500}{100} \right)\,\,=\,\,Rs.\,\,\frac{697500}{100}\,\,=\,\,Rs.\,\,6975\]
Therefore, Rahul spend every month in terms of rupees
= Earned money ? Saving money = Rs. 15500 ? Rs. 6975 = Rs. 8525.
Simple Interest
We all need money, but money is not free to borrow. People can always find a use for money, so it costs to borrow money. When we borrow ?money? form a bank, we pay some hire charges for its used. This hire charge is named as ?Interest.? Similarly, if we deposit money in a bank, the bank pays us ?Interest? and it uses our money as it likes.
The money deposited or borrowed is called the Principal (P). If the interest is paid every year and is not added to the principle together with the interest is called Amount (A).
So we have, Amount = Principal + Simple Interest, or A = P + I
Here, Simple Interest \[=\,\,\frac{\Pr inciple(P)\times Time(T)\,\times Rate(R)}{100}\]
Or, \[\mathbf{S}\mathbf{.I}\mathbf{.}\,\,\mathbf{=}\,\,\frac{\mathbf{P\times T\times R}}{\mathbf{100}}\mathbf{.}\]
Find the simple interest on 6000 for 3 years at 8% interest per annum. What will be the amount paid at the end of 3 years?
Solution:
Principle (P) = Rs. 6000, Rate of Interest (R) = 8% p.a.
Time (T) = 3 years. So, Simple Interest (I) \[\frac{P\times R\times T}{100}\]
\[=\,\,Rs.\left( \frac{6000\times 8\times 3}{100} \right)\,\,=\,\,Rs.\frac{144000}{100}\,\,=\,\,Rs.1440\]
So, amount (A) = P + I = Rs. 6000 + Rs. 1440 = Rs. 7440
Profit and Loss
The amount which a shopkeeper pays of buy an article is called Cost Price (C.P).
The additional expenses like transportation charges, Octroi, Labour changes, wages, etc. are called Overhead Charges. They from part of C.P.
The amount which a shopkeeper receives from the customer by selling an article is called Selling Price (S.P).
When selling Price (S.P) is greater than cost price (C.P) or S.P
When selling price (S.P) is less than cost price (C.P) or S.P<C.P., there is a loss. So, Loss = C.P. ? S.P.
Remember that profit or loss is always calculated on the cost price including overhead charges (if given). So, we have four relations in between S.P. and C.P.
(i) S.P. = C.P Profit (gain) (ii) S.P. = C.P ? Loss
(iii) C.P = S.P + Loss (iv) C.P. = S.P. ? Profit (gain)
A book Seller buys books at Rs. 50 each and sells them at Rs. 57.50 each. If he sells 200 books in a week, find his weekly profit in rupees.
Solution: Cost price of a book = Rs. 50. Selling price of a book = Rs. 57.50
Since S.P. is greater than C.P.
So, Profit on one book = S.P. ? C.P. = Rs. 57.50 ? Rs. 50 = Rs. 7.50
Now, the number of books sold out in a week = Rs. \[(7.50\times 200)\,\,=\,\,Rs.\,1500.\]
Therefore, the weekly profit of the book seller = Rs. 1500.
Profit or Loss Percentage
The percentage profit or percentage loss made from a transaction is founded by using the formula below.
Profit percentage \[=\,\,\frac{\Pr ofit\times 100}{Cost\,\,\Pr ice},\]Loss percentage \[=\,\,\frac{Loss\times 100}{Cost\,\,\Pr ice},\]
Converting Profit or Loss Per Cent to Rupees
When percentage of profit or percentage of loss is given, we use the following formulae to calculate profit and loss respectively.
\[\operatorname{Pro}fit\,\,=\,\,\frac{\Pr ofit\,\,in\,\,per\,\,cent\times C.P.}{100},\] \[\operatorname{Pro}fit\,\,=\,\,\frac{\Pr ofit\,\,in\,\,per\,\,cent\times C.P.}{100},\]
Aman bought a bicycle for Rs. 7300 and sold it after \[\mathbf{1}\frac{\mathbf{1}}{\mathbf{2}}\] years at a loss of 25%. What is the loss incurred by him? What is the selling price of the bicycle?
Solution: Cost price (C.P) of the bicycle = Rs. 7300
Percentage of loss = 25%
So, Loss = 25% of C.P. = 25% of Rs. 7300
= \[Rs.\left( \frac{25}{100}\times 7300 \right)\,\,=\,\,Rs.\left( \frac{182500}{100} \right)\,\,=\,\,Rs.\,1825\]
So we have, S.P. = C.P ? Loss = Rs. 7300 ? Rs. 1825 = Rs. 5475.
Therefore, selling price of the bicycle is Rs. 5475.
Ratio
Ratio is all about comparing quantities. A ratio can be cancelled in the same way as fractions, in order to reduce to its lowest term. A ratio can also be expressed as fraction.
Convert to the same unit and write the ratio for the following.
(i) 4 hours to 48 minutes
(ii) 350 ml to \[\mathbf{1}\frac{\mathbf{1}}{\mathbf{2}}\,\mathbf{L}\]
Solution:
(i) 1 hour = 60 minutes, 4 hours = 60\[\times \]4 minutes
Therefore, ratio of the 4 hour to the 48 minutes
\[=\,\,\frac{4\,\,hours}{48\,\,\min utes}\,\,=\,\,\frac{240\,\,\min ute}{48\,\,\operatorname{minute}}\,\,=\,\,\frac{5}{1}\,\,=\,\,5:1.\]
(ii) \[1\frac{1}{2}L\,\,=\,\,\frac{3}{2}\,\,L,\,\,1\,L\,=\,\,1000\,\,ml\]
So, \[\frac{3}{2}\,L\,\,=\,\,1000\times \,\,\frac{3}{2}\,ml\,\,=\,\,1500\,\,ml\]
Therefore, ratio of the 350 ml to the \[1\frac{1}{2}\,\,L\]
\[=\,\,\frac{350}{1\frac{1}{2}\,L}\,\,=\,\,\frac{350\,ml}{1500\,ml}\,\,=\,\,\frac{7}{30}\,\,=\,\,7:30\]
Compare 2:3 and 3:5.
Solution: Here, 2:3 = \[\frac{2}{3}\] and 3.5 =\[\frac{3}{5}\]. L.C.M. of 3 and 5 is 15.
Now, \[\frac{2}{3}\,\,=\,\,\frac{2\times 5}{3\times 5}\,\,=\,\,\frac{10}{15},\] and \[\,\frac{3}{5}\,\,=\,\,\frac{3\times 3}{5\times 3}\,\,=\,\,\frac{9}{15},\]
Clearly, \[\frac{10}{15}\,>\,\frac{9}{15},\] because 10>9. So, \[\frac{2}{3}\,>\,\frac{3}{5},\] or 2:3 > 3:5
Proportion
Proportion says that two ratios or fractions are equal. It means when two ratios represent equal quantities, they are said to be in proportion, Each set of ratios may have different quantities, but their proportion may be the same. For example.
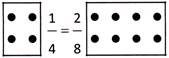
So, 1 out of 4 is equal to 2 out of 8. Here, the ratio are the same, so they are in proportion. Ratios given above are 1:4 and 2:8. If we reduce 2:8, it becomes 1:4. The two end terms are called the extremes and the two inner terms are called means. The symbol, used for proportion is ?: :?, that means ?is in proportion to?. In this proportion 1:4 : : 2:8, where, 1 and 8 are extremes and 4 and 2 are means.
Another way to finding out whether two ratios are in proportion is to multiply by two extremes together and the two means together. If their products are equal, then the two ratios are said to be in proportion.
For example, in 1 : 4 : : 2 : 8, 1 \[1\,\,\times \,\,8\,\,=\,\,8\] and \[4\,\,\times \,\,2\,\,=\,\,8\]
So, \[1\,\,\times \,\,8\,\,=\,\,4\,\,\times \,\,2.\] Therefore, 1, 4, 2 and 8 are in proportion.
An iron rod 8 meters long weighs 480 grams. What is the weight of a similar bar that is 3 meters long?
(a) 120 grams (b) 180 grams
(c) 90 grams (d) 240 grams
(e) None of these
Answer (b)
Explanation:
Length of given rod = 8 meters. Weight of given rod = 480 grams
Now, we have to find the weight of the iron rod whose length is 3 meters, let it is x grams.
So, \[\frac{8}{3}\,\,=\,\,\frac{480}{x},\] or, \[\frac{8}{3}\times \frac{3}{8}\,\,=\,\,\frac{480}{x}\,\times \,\frac{3}{8}.\] Or, \[1\,\,=\,\,\frac{60\times 3}{x},\]
Or, \[x\,\,=\,\,60\,\,\times \,\,3\,\,=\,\,180\] grams
Verification: \[\frac{8}{3}\,\,=\,\,\frac{480}{180},\] or, \[\frac{8}{3}\,\,=\,\,\frac{8\times 60}{3\times 60},\] or, \[\frac{8}{3}\,\,=\,\,\frac{8}{3}\]
So, we have, 8, 3, 480 and 180 are in proportion.
Unitary Method
Unitary Method is also known as the method of one. The term ?Unitary Method? is a technique which has evolved from the concept of ?unit? which means ?of one?.
In Unitary Method:
· To get more value, we multiply.
· To get less value, we divide.
This topic is all about finding the cost of two or more things when the cost of one is given and vice versa.
Direct Variation
When two variable quantities (or things) are related to each other in such a way that on increase in one results in an increase in the other, or a decrease in one results in a decrease in the other, it is said to be in Direct Variation, or Direct Proportion, or Directly Proportional. Remember that a direct change in one will result in a similar change in other. For example, cost of 1 apple is Rs. 5. Cost of 5 apples is Rs. 25. Cost of 6 apples = Rs. 30. Cost of 12 apples = Rs. 60. Here, the cost goes up when the number of apples increase and the cost comes down when the number of apples decreases.
A car travels 288 km in 6 hours. What distance will it travel in 9 hours at the same speed?
(a) 512 km (b) 496 km
(c) 432 km (d) 464 km
(e) None of these
Answer (c)
Explanation:
|
Distance |
Time taken |
Distance |
Time taken |
|
288 km |
6 hours |
x |
9 hours |
So we have, 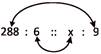
Or, \[6\,\,\times \,\,x\,=\,\,9\,\,\times \,\,288,\] or, \[6x\,\,=\,\,2592,\] or \[x\,\,=\,\,\frac{2592}{6},\] or, x = 432
Therefore, the car will travel 432 km in 9 hours at the some speed.
Verification: \[6\,\,\times \,\,432\,\,=\,\,2592\] and \[9\,\,\times \,\,288\,\,=\,\,2592\]
Hence, \[6\,\,\times \,\,432\,\,=\,\,9\,\,\times \,\,288.\]
Inverse Variation
When two variable quantities (or things) are related to each other in such a way that an increase in one, results in a decrease in the other, or a decrease in one, results in an increase in the other, it is said to be in Inverse Variation, or Inverse Proportion or Inversely Proportional. It is a relationship between two variable quantities in which the product is unchanged or constant. For example, if 4 men take 12 days to finish a job, and we have to find how long would it take for 6 men to finish the same job, first we have to assume that all men have the same capacity to do work. So, when more men are put on the job, naturally the work will get done faster. We have, more men means less time is taken to finish the job. Here when one variable increases, the other will decrease and, when one variable decreases, the other will increase. Let calculate it.
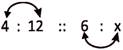
In Inverse variation, the product of the first two terms should be equal to the product of the next two terms.
Hence, \[4\,\,\times \,\,12\,\,=\,\,6\,\,\times \,\,x,\]or, 6x = 48, or, \[x\,\,=\,\,\frac{48}{6},\] or, x = 8.
So, if 4 men take 12 days to finish a job, then 6 men take only 8 days to finish the same job.
Verification: \[4\,\,\times \,\,12\,\,=\,\,48\] and \[6\,\,\times \,\,8\,\,=\,\,48,\] so, \[4\,\,\times \,\,12\,\,=\,\,6\,\,\times \,\,8.\]
A car travels for 3 hours and covers a distance at a speed to 60 km/h. If it travels at the speed of 90 km/h, how much time will it take to cover the same distance?
(a) \[2\frac{1}{2}\] hours (b) \[1\frac{1}{2}\] hours
(c) 4 hours (d) 2 hours
(e) None of these
Answer (d)
Explanation:
Here, we have to find the time taken by the car when speed is increased but the distance is uncharged. So, it is based on inverse variation.
|
Time Taken |
Speed |
Time Taken |
Speed |
|
3 hours |
60 km/h |
x |
90 km/h |
Or, ![]()
Or, \[3\,\,\times \,\,60\,\,=\,\,x\,\,\times \,\,90,\] or, \[90x\,\,=\,\,180,\] or, \[x\,\,=\,\,\frac{180}{90},\] or x = 2
So, the car will take 2 hours to cover the same distance at the speed at 90 km/h.
Average
A number that is calculated by adding quantities together and then dividing the total by the number of quantities is called ?average?. It is also called ?mean?. It is a calculated for central value of a set of the numbers of quantities.
So, \[Average\,\,=\,\,\frac{Sum\,of\,number\,(x)}{Sum\,of\,addents\,(n)}\]
Find the average of the given numbers.
7, 9, 11, 13, 17, 18
(a) 12.0 (b) 12.5
(c) 11.5 (d) 13.5
(e) None of these
Answer (b)
Explanation: Sum of numbers = 7 + 9 + 11 + 13 + 17 + 18 = 75
Number of addends = 6.
So, \[Average\,\,=\,\,\frac{Sum\,of\,number\,(x)}{Sum\,of\,addents\,(n)}\,\,=\,\,\frac{75}{6}\,\,=\,\,12.5\]
Distance, Time and Speed
Distance: The length of the space between two points is know as distance.
Time: A limited period or interval, as between two successive events is know as time.
Speed: Speed is the distance covered per unit time.
Relation between distance, time and speed is given below:
\[Speed\,\,=\,\,\frac{Dis\operatorname{tance}}{Time}\]
Express the given speed in km/h.
400 meters in 40 Seconds
Solution: As we know, 1 km = 1000 m and 1 hour = 3600 seconds
So, 1 meter \[=\,\,\frac{1}{1000}\] km and 1 second \[=\,\,\frac{1}{3600}\] hour. Now speed \[Speed\,\,=\,\,\frac{Dis\operatorname{tance}}{Time}\]
= Distance \[\div \] Time = \[\left[ \left( 400\frac{1}{1000} \right)\div \left( 40\times \frac{1}{3600} \right) \right]\,\,m/\sec \]
\[=\,\,\left( \frac{400}{1000}\div \frac{40}{3600} \right)\,\,m/\sec \,\,=\,\,\left( \frac{400}{100}\times \frac{3600}{40} \right)\,\,m/\sec \]
\[\frac{1440000}{40000}\,\,m/\sec \,\,=\,\,\frac{144}{4}\,\,m/\sec \,\,=\,\,36\,\,m/sec\]
How long will a lorry take to travel 228 km at the speed of 60 km/h?
(a) 3 hour 12 minutes (b) 3 hours 24 minutes
(c) 3 hours 48 minutes (d) 4 hours 6 minutes
(e) None of these
Answer (c)
Explanation: Given that distance = 228 km
Speed = 60 km/h, \[Time\,\,=\,\,\frac{Dis\tan ce}{Speed}\,\,=\,\,\frac{228}{60}\,\,hours\]
= 3.8 hours = (3 + 0.8) hours
Since, 1 hours = 60 minutes
= 3 hours + 0.8 \[\times \]60 minutes
= 3 hours + 48 minutes = 3 hours 48 minutes
You need to login to perform this action.
You will be redirected in
3 sec
