Area, Perimetre and Volume of Geometrical Figures
Category : 5th Class
Area, Perimetre and Volume of Geometrical Figures
Perimeter
Perimeter is referred as the length of the boundary line, which surrounds the area occupied by a geometrical shape.
Find the perimeter of the following figure.
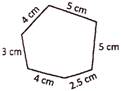
Solution: Perimeter of the figure =
\[4\text{ }cm+3\text{ }cm+4\text{ }cm+2.5\text{ }cm+5\text{ }cm+5\text{ }cm\]\[=23.50\text{ }cm.\]
Perimeter of the Triangles
A triangles has three sides. Perimeter of a triangle is the sum of its all the three sides.
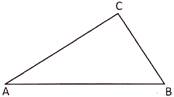
Perimeter of the triangle \[ABC=AB+BC+CA\]
Find the perimeter of the following triangle.
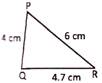
Solution: Perimeter of the triangle PQR
\[\begin{array}{*{35}{l}}
=4\text{ }cm+4.7\text{ }cm+6\text{ }cm \\
=14.7\text{ }cm \\
\end{array}\]
Perimeter of the Quadrilateral
Perimeter of a quadrilateral is the sum of the length of its four sides.
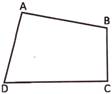
In quadrilateral ABCD, perimeter
\[=AB+BC+CD+DA\]
Find the perimeter of the following quadrilateral.
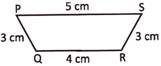
Solution: Perimeter of the quadrilateral
\[=5\text{ }cm+3\text{ }cm+4\text{ }cm+3\text{ }cm=15\text{ }cm\]
Perimeter of Rectangles
Perimeter of a rectangle\[=2\text{ (}Length+Breadth)\].

Find the perimeter of the rectangle whose length is 12 cm and breadth is 8 cm.
Solution: Perimeter of the rectangle
\[=2\text{ (12}+8)=40\,\,cm.\]
Perimeter of Squares
Perimeter of a square\[=4\times side\].

Perimeter of the square ABCD = \[=4\times AB\]
Find the perimeter of the square whose length of one side is 9 cm.
Solution: Perimeter of a square
\[=4\times 9\text{ }cm=36\text{ }cm\]
Area
All the geometrical shapes occupies some space. The occupied space by a geometrical shape is called area of that geometrical shape.

Shaded part in the above figures represent area.
Unit of the area is \[c{{m}^{2}}\] or \[{{m}^{2}}\].
Area of a Triangle
Area of a triangle = \[\frac{1}{2}\times base\times height.\]
Where base is the one side of a triangle and height is length of line segment drawn \[90{}^\circ \]on the base of that triangle.
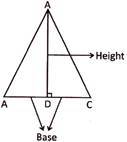
Find the area of the triangle whose base is 75 cm and height is 80 cm.
Solution: Area of the triangle
\[=\frac{1}{2}\times 75cm\times 80cm=3000c{{m}^{2}}\]
Area of a Rectangle
Area of a rectangle = length \[\times \] breadth.

Area of the rectangle PQRS \[=PQ\times QR.\]
Find the area of the rectangle whose length is 17 cm and breadth is 15 cm.
Solution: Area of the rectangle
\[=17\text{ }cm\times 15\text{ }cm=255\text{ }c{{m}^{2}}\]
Area of a Square
Area of a square \[=sid{{e}^{2}}=side\times side\]

Area of the square PQRS\[=PQ\times PQ=P{{Q}^{2}}\]
Find the area of the square whose length of each side is 21 cm.
Solution: Area of the square
\[=21\text{ }cm\times 21\text{ }cm=441\text{ }c{{m}^{2}}\]
Volume
In our daily life the number of things is stored in different kinds of container. Holding capacity of a container is called volume.


![]()


Volume of a Cuboid
Volume of a cuboid =\[length\times breadth\times height=lbh\].
Where, length = AB, breadth = AE and height = BC
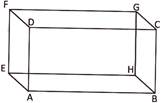
Volume of the cuboid ABCDEFG\[=AB\times BC\times AE.\]
Find the volume of the cuboid whose length, breadth and height are 15 cm, 13 cm and 14 cm respectively.
Solution: Volume of the cuboid
\[=15\text{ }cm\times 13\text{ }cm\times 14\text{ }cm=2730\text{ }c{{m}^{3}}\]
Volume of a Cube
Volume of a cube \[=sid{{e}^{3}}=side\times side\times side\]
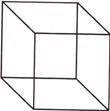
Find the volume of the cube whose length is 19 cm.
Solution: Volume of the cube
\[=19cm\times 19cm\times 19cm=6859c{{m}^{3}}\]
You need to login to perform this action.
You will be redirected in
3 sec
