5th Class Mathematics Geometrical Figures Quadrilateral

Quadrilateral

Category : 5th Class

Quadrilateral

The geometrical figure having four sides is called quadrilateral.

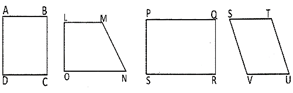
Properties of Quadrilateral

A quadrilateral has:

(i) Four sides

(ii) Four angles

(iii) Four vertices

Sides of the quadrilateral ABCD are AB, BC, CD, and AD.

Angles of the quadrilateral are ZABC, ZBCD, \[\angle CDA,\]and \[\angle DAB.\] Vertices of the quadrilateral ABCD are point A, point B, point C and point D.

Types of Quadrilateral

In this chapter we will study about two types of quadrilateral

(i) Rectangle

(ii) Square

Rectangle

Rectangle is a quadrilateral in which

(i) All angles are of 90°

(ii) Opposite sides are equal.

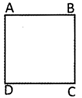
ABCD is a rectangle in which

(i)\[\angle A=\angle B=\angle C=\angle D={{90}^{o}}\]

(ii) AB=CD=7 cm, and BC=AD=5cm.

Square

Square is a quadrilateral in which

(i) All angles are of \[{{90}^{o}}\]

(ii) All sides are equal.

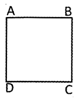
ABCD is a square in which

(i)\[\angle A=\angle B=\angle C=\angle D={{90}^{o}}\]

(ii) AB = BC = CD = DA = 6 cm.

Circle

Circle is a close curved line whose all points are at the same distance from a given point in a plane.

Centre of a Circle

The point from which all the points of the curved line are at the same distance is called centre of the circle.

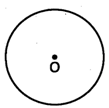
In the given figure, 0 is the centre of the circle.

Radius of a Circle

Distance between the centre and the curved line of a circle is called radius of the circle.

In the given figure, OA is the radius of the circle

Note: All the radius of a circle are equal in length

Chord of the circle

Any line segment which joins the two points of the curved line of a circle is called chord of the circle.

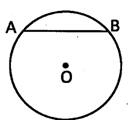
In the figure, AB is the chord of the circle

Diameter of the Circle

The longest chord of a circle is called diametre of the circle. In oth8er word the chord which passes through the centre is called diametre of the circle.

In the figure, AB is the diameter of the circle

Note: All the diameter of a circle are equal in length

Relation between Radius and Diameter of the Circle

In a circle, diameter is twice of the radius. Let radius of a circle is r then diameter of the circle is 2r.

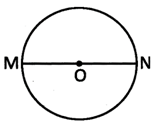
In the figure, OM and ON are the radius of the circle whereas MN is the diameter of the circle. We can see, MN = OM + ON..........

(i) We know that all the radius of a circle is equal in length Thus OM = ON..........

(ii) So , we can write the equation (i) as following MN = OM + OM or MN = ON + ON Thus MN = 20M or MN = 20N Thus, we see that the diametre of a circle is twice of the radius

Radius of a circle is 4.5 cm. Find the diametre of the circle.

Solution:

Diametre\[=2\times \]radius \[=2\times 4.5\text{ }cm\] \[=9\text{ }cm.\]

Triangle is a polygon with least number of sides
The polygon which has 12 sides is called dodecagon

Point indicates a particular location.
Line segment is a fraction of line.
Length of a line segment can be measured.
Ray is considered as the extension of a line segment in one direction.
Length of ray cannot be measured.
Line is considered as the extension of a line segment up to infinity in either direction.
Angle is inclination bet6ween two rays which has common end point.
Acute angle measures between \[{{0}^{o}}\]and \[{{90}^{o}}\]whereas obtuse angle measures between \[{{90}^{o}}\]and \[{{180}^{o}}\].
Triangle is a close geometrical shape with three sides.
Quadrilateral is a close geometrical shape with three sides.
Quadrilateral is a close geometrical shape with four sides.

Which one of the following is defined as the shortest distance between two points?

(a) Line

(b) Line segment

(d) Ray

(e) None of these

Answer (b)

Explanation

Line segment is defined as the shortest distance between two points. Therefore, option (b) is correct and rest of the options is incorrect.

Sides of a triangle are line segments" which one of the following points justify the statement?

(a) Sides of a triangle lie between two vertices and their length can be measured, therefore, sides of a triangle are line segments

(b) A triangle can be prepared by using only line segments instead line or rays, therefore, sides of a triangle are line segments

(c) A triangle lies within a boundary and the boundary is of finite length, therefore, sides of a geometrical figure are line segments

(d) There are infinite number of points on a particular sides, therefore, sides of a triangle are line segments.

(e) None of these

Answer: (a)

How many lines are there in the following figure?

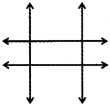
(a) 1

(b) 2

(d) 4

(e) None of these

Answer: (d)

Robert makes a line segment and put an arrow at one end of it. He actually makes a.

(a) Point

(b) Line

(d) Ray

(e) None of these

Answer: (d)

Length of which one of the following can be measured?

(a) Point

(b) Line

(d) Ray

(e) None of these

Answer: (c)

If angle BOC is equal to 90° then the angle DOB is a

(a) Acute angle

(b) Obtuse angle

(d) Straight angle

(e) None of these

Answer: (b)

Explanation

It is clear from the figure that angle DOB is greater than \[{{90}^{o}}.\]

In an isosceles triangle each of the equal angles is of 60°. Then the third angle of the triangle is a:

(a) Acute angle

(b) Obtuse angle

(d) Straight angle

(e) None of these

Answer: (a)

Explanation

Let the measurement of the third angle \[=X\]

Sum of the angles of the triangle \[={{60}^{o}}+{{60}^{o}}+X\] \[X=60{}^\circ \]

Thus X is a acute angle.

A pole is standing vertically upward on the ground. Name the angle whichthe pole is making with the ground.

(a) Right angle

(b) Acute angle

(d) Straight angle

(e) None of these

Answer: (a)

In a rectangle, sum of any two angles is a:

(a) Right angle

(b) Acute angle

(d) Straight angle

(e) None of these

Answer: (d)

In the following triangle ABC, angle BAC is a:

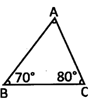
(a) Right angle

(b) Acute angle

(d) Straight angle

(e) None of these

Answer: (b)

We have already studied various shapes like point, line, linesegment etc. Now let us describe the closed shapes bounded by the line segments.

How many right angles are there in a rectangle?

(a) 1

(b) 2

(d) 4

(e) None of these

Answer: (d)

Explanation

Rectangle is a quadrilateral whose all four angles are right angles.

Jack: The following triangle is a equilateral triangle.

Cody: It is also a isosceles triangle. Who of the above is correct?

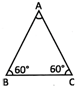
(a) Jack

(b) Cody

(d) Both are incorrect

(e) None of these

Answer: (c)

Explanation

The above given triangle is an equilateral triangle and all the equilateral triangles are also isosceles triangle.

The line segment which joins two points of the line of a circle is called.

(a) Radius

(b) Diameter

(d) Centre

(e) None of these

Answer: (c)

Which one of the following is not true about a rectangle?

(a) All the angles of a rectangle are right angles.

(b) Opposite sides of a rectangle are equal.

(d) All the sides of a rectangle are equal.

(e) None of these

Answer: (d)

The following given triangle is a:

(a) Scalene triangle

(b) Isosceles triangle

(d) All of these

(e) None of these

Answer: (a)

Angle

5th Class Mathematics Geometrical Figures Quadrilateral

Quadrilateral

Other Topics