Geometry
Category : 5th Class
Geometry
A group of points in a straight path, extending on both sides infinitely form a line. Two points on the line denote it.
![]()
A line \[\overleftrightarrow{\text{AB}}\] is read as line AB'.
\[\overleftrightarrow{\text{AB}}\]=\[\overleftrightarrow{\text{BA}}\]
A part of a line with two end points is called a line segment. It has a definite length.
![]()
Line segment
A line segment PQ is written as PQ.
\[\overline{\text{PQ }}\text{= }\overline{\text{QP}}\]
A part of a line, which extends infinitely in one direction only, from a point, is a ray. The point is called the end-point of the ray.
![]()
A ray OP is written as 0?. A ray is denoted by writing the initial point first.
So, \[\overrightarrow{\text{OP}}\ne \overrightarrow{\text{PO}\text{.}}\]
Two rays or line segments with a common end-point form an angle.
The common end-point is called the vertex of the angle and rays or line segments are called arms of the angle.
The unit of the angle is degree denoted by a small ° on the measure.
e.g., \[\angle \text{AOB}\]=47°
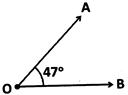
\[\overrightarrow{\text{OA}}\] and \[\overrightarrow{\text{OB}}\] form an angle AOB. 0 is the vertex of \[\angle \text{AOB}\]and \[\overrightarrow{\text{OA}}\]and \[\overrightarrow{\text{OB}}\] are its arms or sides.
Z AOB is the same as Z BOA. Only vertex can also be used to denote an angle. Thus ZA means the angle whose vertex is A.
Types of Angles:
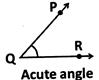
(a) An angle whose measure is between 0° and 90° is called an acute angle.
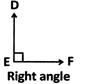
(b) An angle whose measure is 90° is called a right angle.
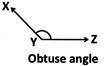
(c) An angle whose measure is between 90° and 180° is called obtuse angle.
![]()
In the given figure, B, F, and E are collinear, while A, C and D are non-collinear points.
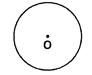
The centre of a circle is usually denoted as 0.
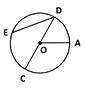
In the figure, OA = OC = OD = radius
Diameter = 2 x Radius
All the diameters of a circle are of the same lengths.
Infinitely many diameters can be drawn in a circle.
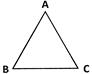
Note: AABC can also be denoted ABCA or as ACAB.
(a) A triangle can be drawn only when the three given points are non-collinear.
(b) A triangle has three vertices, three sides and three angles.
(c) In the figure, the three line segments AB, BC and CA are the three sides of ?ABC.
\[\angle \]A, \[\angle \]B and \[\angle \]C are its three angles and A, B and C are its vertices.
(a) The sum of the lengths of any two sides of a triangle is greater than the length of its third side. AB + BC > AC
(b) The difference of the lengths of any two sides of a triangle is smaller than the length of the third side. AB - BC < AC
(c) The sum of the measures of three angles of a triangle is 180°.
(d) In a triangle ABC, \[\angle \]ABC + \[\angle \]BAC + \[\angle \]BCA = 180°.
(a) A quadrilateral is a simple closed figure bounded by four line segments.
![]()
(b) A quadrilateral has four sides, four vertices, four angles and two diagonals (the line joining the opposite vertices.)
(c) The sum of measures of the four angles of a quadrilateral is 360°.
(a) Parallelogram:
A parallelogram is a quadrilateral whose opposite sides are parallel and equal.
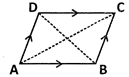
AB is parallel to DC. AC and BD are the diagonals.
BC is parallel to AD. AB = DC and BC = AD.
(b) Rectangle:
A rectangle is a parallelogram in which all the angles are right angles.
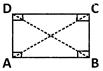
AC and BD are the diagonals. AB = DC and AD = BC. \[\angle \]A =\[\angle \] B = \[\angle \]C = 90°
(c) Square:
A square is a rectangle in which all sides are equal. AB = BC = CD = DA
AC and BD are the diagonals.
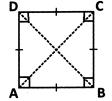
\[\angle \]A= \[\angle \]B= \[\angle \]C= \[\angle \]D=90°
(d) Rhombus:
A rhombus is a parallelogram in which all the sides are equal
AB = BC = CD = DA
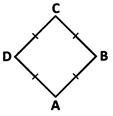
AC and BD are the diagonals.
(e) Trapezium:
A quadrilateral is called a trapezium if a pair of its opposite sides are parallel.
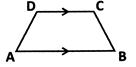
AB is parallel to DC.
You need to login to perform this action.
You will be redirected in
3 sec
