5th Class Mathematics Operations on Numbers Operations on Numbers

LEARNING OBJECTIVE

This lesson will help you to:—

• study and understand about the operation of numbers including additions, subtraction, multiplication and
• learn and understand about the importance of place value in performing operations of numbers.
• study and learn about the operation of fractional and decimal numbers.
• learn to use the operations in order.

Real - Life Examples

• Addition and subtraction are used in the calculations of money.
• We use division when we have to divide something equally.

Example:  Pizza can be divide into 8 pieces so that all the four friends can eat two slices of pizza each.

• Subtraction can also be viewed as addition of signed numbers. Extra minus signs simply denote additive inversion. Then we have

3-(-2) = 3 + 2 = 5

• The study of numbers and its operations is called as algorism.

QUICK CONCEPT REVIEW

What are operations?

An operation is an action or procedure which produces a new value from one or more input values, called "operands".

Operations such as addition, subtraction, multiplication and division are binary operations since they involve two or more values.

The Basic Operations

Historical preview

• The earliest written records indicate the Egyptians and Babylonians used all the elementary arithmetic operations as early as 2000 B.C
• Modern methods for four fundamental operations (addition, subtraction, multiplication and division) were first devised by Brahmagupta of India.

ADDITION

• Addition is bringing two or more numbers (or things) together to make a new total.
• Other names for Addition are Sum, Plus, Increase, Total.
• And the numbers to be added together are called the "Addends"

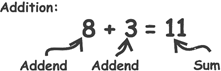
Properties for Addition

1. Commutative property of addition - It states that changing the order of the addends will not affect the sum.

                           a + b = b + a

2. Associative property of addition - It states that changing the groupings of the addends will not affect the sum.

                         a + (b + c) = (a + b) + c

3. Identity Property of Addition - It states that when you add 0 to any real number, the sum is the number itself.

                        a + 0 = a       

SUBTRACTION                     

Subtraction is taking one number away from another.

Minuend: The number that is to be subtracted from.

Subtrahend: The number that is to be subtracted.

Difference: The result of subtracting one number from another.

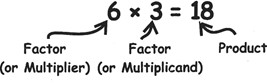
MULTIPLICATION

Multiplication in its simplest form is repeated addition.

Misconcept / Concept

Misconcept: Dividing a number by 0 gives 0. Example: 3/0=0

Concept: We know that 0/3=0. 

Conveniently. We also assume the same result for 3/0. This is not true as 3/0 is undefined.

Misconcept: Zero divided by zero is equal to 1. i.e. 0/0 = 1.

Concept:  We all are aware that 3/3, 5/5, -10/-10 result in 1. As long as we see fraction in the form of a/a, we will expect an answer of 1. This however does not hold when a = 0 as 0/0 is undefined.

Here we see that 6+6+6 (three 6s) make 18.

It could also be said that 3+3+3+3+3+3 (six 3s) make 18.

But you can also multiply by fractions or decimals, which goes beyond the simple idea of repeated addition:

Example: 3.5 x 5 = 17.5 which is 3.5 lots of 5, or 5 lots of 3.5

Properties for Multiplication

1. Commutative Property of Multiplication - It states that changing the order of the factors will not affect the product.

                      a x b= b x a

2. Associative Property of Multiplication - It states that changing the groupings of the factor will not affect the product.

                  a x (b x c) = (a x b) x c

3. Identity Property of Multiplication - It states that when you multiply any number by 1 the result is the number itself.

                     a x 1 = a

4. Zero Property of Multiplication - It states that when you multiply any number by 0 the result is O.

                       a x 0 = 0

DIVISION

• Division is splitting into equal parts or groups.
• We use the - symbol, or sometimes the / symbol to symbolise divide.

 \[12\div 3=4\]

        12/3=4

• Division is the opposite of multiplying.
• There are special names for each number in a division:

DIVIDEND - DIVISOR = QUOTIENT

• Example: 12-3=4, here

12 is the dividend, 3 is the divisor, 4 is the quotient.

ORDER OF OPERATIONS

• Do things in brackets first.
• Exponents (powers, roots) before multiply, divide, add or subtract.
• Multiply or divide before you add or subtract.
• Otherwise just go left to right.
• These steps are summarized as BODMAS.

     B         Brackets first

     O        Orders (i.e. Powers and Square  

              Roots, etc.)

    DM     Division and Multiplication (left- 

                 to- right)

    AS      Addition and Subtraction (left-to-

              right)

• Divide and multiply rank equally (and go left to right).
• Add and Subtract rank equally (and go left to right).

PLACE VALUE

• While doing the operation of numbers, place value is very important and should be taken into account while performing addition, subtraction, multiplication and division.

OPERATIONS OF FRACTIONS AND DECLMAL NUMBERS

The fractional and decimal numbers are operated the same way as whole numbers.