Geometry
Category : 5th Class
Geometry
Learning Objectives
Point
To show a particular location, a dot (.) is placed over it, that dot is known as a point.
Line Segment
A line segment is defined as the shortest distance between two fixed points. For example
![]()
It is denoted as AB.
Ray
It is defined as the extension of a line segment in one infinitive direction. For example:
![]()
It is denoted as AB.
Line
A line is denned as the extension of a line segment Infinitive in either direction
![]()
It is denoted as AB ![]()
Angle
Inclination between two rays having common end point is called an angle.
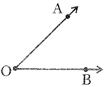
Angle is measured in degree. Symbol of the degree is "o" and written as \[a{}^\circ \], where a is the measurement of the angle.
Types of Angle
There are different types of angles.
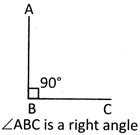
Right Angle
An angle whose measure is exactly \[90{}^\circ \] is a right angle.
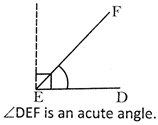
Acute Angle
An angle whose measure is less than \[90{}^\circ \] is an acute angle.
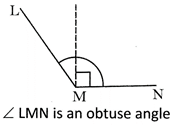
Obtuse Angle
An angle whose measure is greater than \[90{}^\circ \] but less than \[180{}^\circ \] is an obtuse angle.
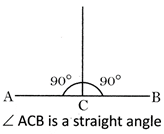
Straight Angle
An angle whose measure is \[180{}^\circ \] is a straight angle.
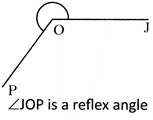
Reflex Angle
An angle whose measure is greater than \[180{}^\circ \] but less than \[360{}^\circ \] is a reflex angle.
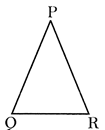
Triangle
A geometrical shape having three closed sides are called triangle.
Triangle can be classified:
(a) On the basis of sides
(b) On the basis of angles
On the basis of sides, triangle is of three types:
(i) Equilateral Triangle
It is a triangle in which all the three sides are equal.
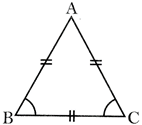
(ii) Isosceles Triangle
In this type of triangle two of the three sides are equal.
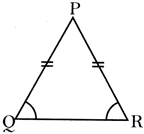
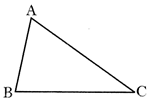
(iii) Scalene Triangle
In this triangle all the sides are unequal.
B. Angle Based Classification
On the basis of angles, triangles are of three types.
(i) Acute Angled Triangle
A triangle whose all the angles are acute is called acute angled triangle.
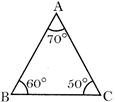
(ii) Obtuse Angled Triangle
A triangle in which one angle is an obtuse angle is called an obtuse angled triangle.
(iii) Right Angled Triangle
A triangle in which one angle is \[90{}^\circ \] is called a right angled triangle.
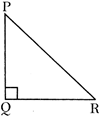
PQR is a right–angled triangle as it contains a right angle (\[\angle PQR\])
Quadrilateral
The geometrical figure having four closed sides is called a quadrilateral.

Types of Quadrilateral
There are two types of quadrilateral;
(i) Rectangle
(ii) Square
Rectangle
A rectangle is a quadrilateral in which:
(i) All angles are of \[90{}^\circ \];
(ii) Opposite sides are equal.

Square
A square is a quadrilateral in which:
(i) All angles are of \[90{}^\circ \];
(ii) All sides are equal.

Circle
A circle is a close curved line whose all points are at the same distance from a given point in a plane.
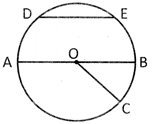
Here, O is the centre of the circle.
Chord
It is a line segment joining two distinct points of the circle. Here, DE is a chord of the circle.
Radius
Radius of a circle is half of the diameter.
OA, OB, and OC are radius of the circle.
Cuboid
A cuboid is a box shaped solid object. It has six flat faces, which are rectangular in shape

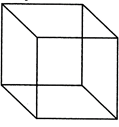
Cube
A cube is also a box shaped solid object with six faces, which are square in shape
Commonly Asked Question
2. Sum of 5 angles of a hexagon is \[\mathbf{570}{}^\circ \]. What is the remaining angle?
(a) \[120{}^\circ \] (b) \[130{}^\circ \]
(c)\[150{}^\circ \] (d) \[170{}^\circ \]
(e) None of these
Answer: (c)
Explanation: A hexagon has 6 sides.
So, the sum of all interior angles = (Number of sides – 2)\[\times 180{}^\circ =\left( 62 \right)~180{}^\circ =4~\times 180{}^\circ =720{}^\circ \]
Hence, the remaining angles = Sum of all 6 angles – Given sum of 5 angles \[=720{}^\circ 570{}^\circ =150{}^\circ \]
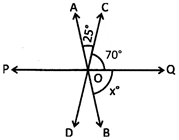
3. If \[\angle POQ\]is a right angle in the given figure, then find the value of \[\mathbf{x}{}^\circ
\]
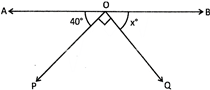
a)\[45{}^\circ \] (b) \[50{}^\circ \]
(c)\[40{}^\circ \] (d) \[55{}^\circ \]
(e) None of these
Answer: (b)
Explanation: Given that \[\angle POQ=90{}^\circ \], and \[\angle AOP=40{}^\circ \]
\[\angle AOP+\angle POQ+\angle BOQ=180{}^\circ \] (Linear pair)
Or, \[40{}^\circ +90{}^\circ +x{}^\circ =180{}^\circ \] or, \[x{}^\circ =180{}^\circ 130{}^\circ =50{}^\circ \].
4. In the figure given below, find the value of \[\mathbf{x}{}^\circ \].
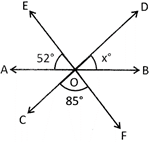
(a) \[42{}^\circ \] (b) \[43{}^\circ \]
(c) \[57{}^\circ \] (d) \[39{}^\circ \]
(e) None of these
Answer: (b)
Explanation: \[\angle EOD=\angle COF=85{}^\circ \] (Vertically Opposite Angles)
Now, for the straight line \[AB,\angle AOE+\angle EOD+\angle BOD=180{}^\circ \]
(Linear pair or supplementary adjacent angles)
So, \[52{}^\circ +85{}^\circ +x{}^\circ =180{}^\circ ,\] or \[x{}^\circ =180{}^\circ 137{}^\circ =43{}^\circ \]
5. If an angle is its own complementary angle, then its measure is:
(a) \[30{}^\circ \] (b) \[45{}^\circ \]
(c) \[60{}^\circ \] (d) \[90{}^\circ \]
(e) None of these
Answer: (b)
Explanation: Since the angle is its own complementary angle, both angles must be equal. So \[x{}^\circ \] is complementary of \[x{}^\circ \].
So, \[x{}^\circ +x{}^\circ =90{}^\circ \] or, \[x{}^\circ +x{}^\circ =45{}^\circ +45{}^\circ \] or,\[x=45{}^\circ \].
You need to login to perform this action.
You will be redirected in
3 sec
