Measurement
Category : 5th Class
Measurement
Learning Objectives
Perimeter
Perimeter is referred as the length of the boundary line, which surrounds the area occupied by a geometrical shape.
Perimeters of different geometrical shapes are explained below.
A. Perimeter of a Triangle
A triangles has three sides. Perimeter of a triangle is the sum of its all the three sides.
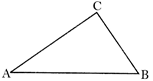
Perimeter of the triangle \[ABC=AB+BC+CA\]
B. Perimeter of a Quadrilateral
Perimeter of a quadrilateral is the sum of the length of its four sides.
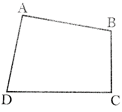
In quadrilateral ABCD, perimeter \[=AB+BC+CD+DA\]
C. Perimeter of a Rectangle
Perimeter of a rectangle = 2 (Length + Breadth).
D. Perimeter of a square \[=\mathbf{4}\times \mathbf{side}\].
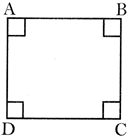
Perimeter of the square \[ABCD=4\times AB\]
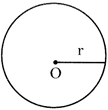
E. Perimeter of a Circle
Perimeter of a circle \[=2\pi r\]
Where \[~\pi =\frac{22}{7}~=3.14\] and r = radius of the circle
Area
All the geometrical shapes occupies some space. The occupied space by a geometrical shape is called area of that geometrical shape.
Shaded part in the above figures represent area.
Unit of area is \[c{{m}^{2}}\]or \[{{m}^{2}}\].
Areas of different geometrical shapes are listed belowA. Area of a Triangle
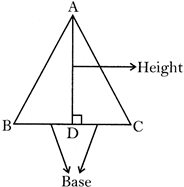
Area of a triangle \[=1/2\times ~\,base~\times \,height\].
Where base is the one side of a triangle and height is the length of the line segment drawn \[90{}^\circ \] on the base of that triangle.
B. Area of a Rectangle
Area of a rectangle\[\text{=length }\!\!~\!\!\text{ }\!\!\times\!\!\text{ }\,\text{breadth}\].

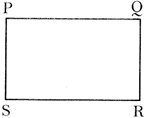
Area of the rectangle \[PQRS=PQ\times QR\]. Where PQ is the length and QR is the breath.
C. Area of a Square
Area of a square \[\text{=sid}{{\text{e}}^{\text{2}}}\text{=side }\!\!~\!\!\text{ }\!\!\times\!\!\text{ }\,\text{side}\]
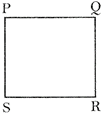
Area of the square \[PQRS=PQ~\times \,PQ=P{{Q}^{2}}\].
D. Area of a Circle
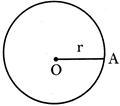
Area of the circle = \[\pi {{r}^{2}}\]
Where \[\pi =\frac{22}{7}=3.14\]
Commonly Asked Questions
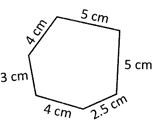
(a) 22.45 cm (b) 23.50 cm
(c) 20.15 cm (d) 15.55 cm
(e) None of these
Answer: (b)
Solution: Perimeter of the figure \[=4\text{ }cm+3\text{ }cm+4\text{ }cm+2.5\text{ }cm+5\text{ }cm+5\text{ }cm=23.50\text{ }cm\].
2. Find the perimeter of the following triangle.
(a) 14.7 cm (b) 13.2 cm
(c) 13.2 c m (d) 16.5 cm
(e) None of these
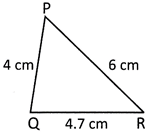
Answer: (a)
Solution: Perimeter of the triangle PQR
\[=4\text{ }cm+4.7\text{ }cm+6\text{ }cm\]
\[=14.7\text{ }cm\]
3. Find the perimeter of the following quadrilateral.
(a) 12 cm (b) 10 cm
(c) 15 cm (d) 19 cm
(e) None of these
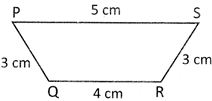
Answer: (c)
Solution: Perimeter of the quadrilateral \[=PS+SR+RQ+QP=5\text{ }cm+3\text{ }cm+4\text{ }cm+3cm=15\text{ }cm\]
4. Find the perimeter of the rectangle whose length is 12 cm and breadth is 8 cm.
(a) 40 cm (b) 20 cm
(c) 15 cm (d) 30 cm
(e) None of these
Answer: (a)
Solution: Perimeter of the rectangle
\[=2\left( 12+8 \right)=40\text{ }cm\].
5. Find the perimeter of the square whose length of one side is 9 cm.
(a) 32 cm (b) 31 cm
(c) 36 cm (d) 15 cm
(e) None of these
Answer: (c)
Solution: Perimeter of a square \[=4~\times \,side\]
\[=4~\times \,9\text{ }cm=36\text{ }cm\]
6. If radius of a circle is 0.35 cm, find the perimeter of the circle.
(a) 2.2 cm (b) 2.1 cm
(c) 2.3 cm (d) 3.1 cm
(e) None of these
Answer: (a)
Solution: Perimeter the circle \[=2\pi r\]
\[=2\times \frac{22}{7}\times 0.35\,\,cm\]
\[=2.2\text{ }cm\]
7. Find the area of the triangle whose base is 75 cm and height is 80 cm.
(a) \[3000\,c{{m}^{2}}\]
(b) \[1500\,c{{m}^{2}}\]
(c) \[3500\,c{{m}^{2}}\]
(d) \[2000\,c{{m}^{2}}\]
(e) None of these
Answer: (a)
Solution: Area of the triangle \[=1/2~\times \,b~\times \,h\]
\[=\frac{1}{2}\times ~75\text{ }cm~\times \,80\text{ }cm=3000\text{ }c{{m}^{2}}\]
8. Find the area of the rectangle whose length is 17 cm and breadth is 15 cm.
(a) \[253\,c{{m}^{2}}\]
(b) \[255\,c{{m}^{2}}\]
(c) \[241\text{ }c{{m}^{2}}\]
(d) \[234\text{ }c{{m}^{2}}\]
(e) None of these
Answer: (b)
Solution: Area of the rectangle \[\text{=l }\!\!~\!\!\text{ }\!\!\times\!\!\text{ }\,\text{b}\]
\[=17\text{ }cm~\times \,15\text{ }cm=255\text{ }c{{m}^{2}}\]
9. Find the area of the square whose length of each side is 21 cm.
(a) \[441\,c{{m}^{2}}\]
(b) \[420\,c{{m}^{2}}\]
(c) \[244\,c{{m}^{2}}\]
(d) \[211\,c{{m}^{2}}\]
(e) None of these
Answer: (a)
Solution: Area of the square \[\text{=side }\!\!\times\!\!\text{ side=21 cm }\!\!~\!\!\text{ }\!\!\times\!\!\text{ }\,\text{21 cm=441 c}{{\text{m}}^{\text{2}}}\]
10. Find the area of the circle whose radius is 0.28 cm.
(a) \[0.2342\,c{{m}^{2}}\]
(b) \[0.2251\,c{{m}^{2}}\]
(c) \[0.2464\,c{{m}^{2}}\]
(d) \[0.2142\,c{{m}^{2}}\]
(e) None of these
Answer: (c)
Solution: Area of a circle \[=2{{r}^{2}}\]
\[=\frac{22}{7}\times ~0.28\text{ }cm~\times \,0.28\text{ }cm=0.2464\text{ }c{{m}^{2}}\]
11. Find the volume of the cuboid whose length, breadth and height are 15 cm, 13 cm and 14 cm respectively.
(a) \[2507\,c{{m}^{2}}\]
(b) \[2730\,\,c{{m}^{2}}\]
(c) \[2302\,c{{m}^{2}}\]
(d) \[2350\,\,c{{m}^{2}}\]
(e) None of these
Answer: (b)
Solution: Volume of the cuboid \[\text{=l }\!\!~\!\!\text{ }\!\!\times\!\!\text{ }\,\text{b }\!\!~\!\!\text{ }\!\!\times\!\!\text{ }\,\text{h}\]
\[=15\text{ }cm~\,\times \,13\text{ }cm\times 14\text{ }cm=2730\text{ }c{{m}^{3}}\]
Volume
In our daily life a number of things are stored in different kinds of containers Holding capacity of a container is called its volume.

Volume of a Cuboid
Volume of a cuboid = length \[\times \] breadth \[\times \] height = Ibh.
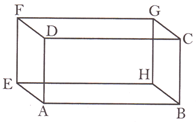
Volume of the cuboid\[ABCDEFG=AB\times AE\times BC\].
Where, length = AB, breadth = AE and height = BC
Volume of a Cube
Volume of a cube \[=sid{{e}^{3}}=side~\times \,side~\times \,side\]
You need to login to perform this action.
You will be redirected in
3 sec
