Volume of Geometrical Figures
Category : 9th Class
A solid has capacity to acquire space.
The space occupied by a solid is called its volume. Sl unit of volume\[~={{m}^{3}}\]
If the volume of a cube is \[1{{m}^{3}},1{{m}^{3}}\] is the space occupied by a cube of sides 1m.
If the volume of the solid is 6 cm3 it means it occupies the space six times of the volume,\[~1c{{m}^{3}}\]
In the picture given below six shapes are combined to each other and length, width and height of every figure is 1 cm, therefore, the total length of the entire picture is 6 cm and width and height is 1cm, hence the volume of the entire picture is six times of the volume of every one.
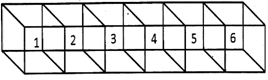
![]() Cube
Cube
The solid figure whose all sides or edges are equal is called cube. In the picture given below the edges of the cube are equal.
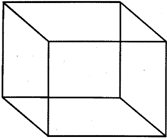
Features of the Cube
(i) A cube has 6 surfaces and shape of every surface is equal.
(ii) A cube has 12 equal edges called sides.
(iii) It has 8 vertices.
Therefore, formula the total surface area of Cube \[=6\times sid{{e}^{2}}\]
Lateral surface area of Cube \[=\text{ }4\times sid{{e}^{2}}\]
Volume of cube = side x side x side = \[{{\left( side \right)}^{3}}\]
![]()
Find the surface area of a cube whose side is 14 cm.
(a) \[1170c{{m}^{2~}}\]
(b) \[1175c{{m}^{2}}\]
(c) \[1176c{{m}^{2}}\]
(d) All of these
(e) None of these
Answer: (c)
Explanation
Side = 14 cm Surface area of a cube \[=6\times {{\text{(}side\text{)}}^{2}}\]
\[=6\times {{(14)}^{2}}c{{m}^{2}}\] \[=6\times 196\text{ }c{{m}^{2}}\]
\[=1176\text{ }c{{m}^{2}}\]
![]() Cuboid
Cuboid
A solid made up of 6 rectangular surfaces is called cuboid. Match box is the example of a cuboid. In the picture given below I is length, b is breadth and h is the height of the cuboid.
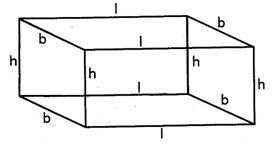
Features of cuboid
(i) A cuboid has 6 rectangular surfaces.
(ii) It has 12 edges.
(iii) A cuboid has 8 vertices.
Therefore the total surface area of a cuboid = Sum of the surface area of its 6rectangular faces
\[=\text{l}\times b\text{ }+\text{l}\times b\text{ }+\text{ }b\times h+b\times h+\text{l}\times \text{ }h\text{ }+\text{ l}\times h\]\[=21b+2bh+21h\]
Therefore the total surface area of cuboid \[=2\left( lb+bh+lh \right)\]
Area of four walls of a cuboid = 2 (breadth \[\times \] height + length \[\times \] height)
Area of four walls of a cuboid \[=2(bh+Ih)\]
Area of four walls of a cuboid \[=2h(l+b)\]
The lateral surface area of a cuboid = The total surface area of four walls.
Volume of cuboid = length \[\times \] breath \[\times \] height \[=l\times b\times h=lbh.\]
![]()
Find the surface area of a chalk box whose length, breadth and height are 10 cm, 6 cm and 3 cm respectively.
(a) \[117c{{m}^{2~}}\]
(b) \[~275c{{m}^{2}}\]
(c) \[216c{{m}^{2}}\]
(d) All of these
(e) None of these
Answer: (c)
Explanation
Length = 10 cm. Breadth = 6 cm. Height = 3 cm
Surface area of the chalk box \[=2(lb+bh+hl)\]
\[=2\left( 10\times 6+6\times 3+3\times 10 \right)c{{m}^{2}}\] \[=2(60+18+30)c{{m}^{2}}=2(108)\text{ }c{{m}^{2}}=216\text{ }c{{m}^{2}}\]

![]() Find the surface area of a cube whose each side is 45 cm.
Find the surface area of a cube whose each side is 45 cm.
(a) \[12150\text{ }c{{m}^{2}}\]
(b) \[11750c{{m}^{2}}\]
(c) \[12160c{{m}^{2~}}\]
(d) All of these
(e) None of these
Answer: (a)
Explanation
Side = 45 cm
Surface area of a cube \[=6\times {{\left( side \right)}^{2}}=6\times {{(45)}^{2}}\,\,cm\] \[=6\times 2025\text{ }c{{m}^{2}}=12150\text{ }c{{m}^{2}}\]
![]() Two cubes each of side 6 cm are placed together. Find the total surface area of the cuboid thus formed.
Two cubes each of side 6 cm are placed together. Find the total surface area of the cuboid thus formed.
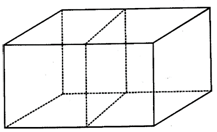
(a) \[760c{{m}^{2}}\]
(b) \[~360c{{m}^{2}}\]
(c) \[12c{{m}^{2}}\]
(d) All of these
(e) None of these
Answer :(b)
Explanation
Length of the cuboid = 12 cm
Width of the cuboid = 6 cm
Height of the cuboid = 6 cm
Total Surface area of the cuboid\[~=2\left( lb+bh+hl \right)\] \[=2\left( 12\times 6+6\times 6+6\times 12 \right)=2\left( 72+36+72 \right)=360\text{ }c{{m}^{2}}\]
![]() The dimensions of an oil container are 25, 25 and 15 cm. Find the cost of the iron sheet for making these 20 containers at the rate of Rs 20 per \[{{m}^{2}}.\]
The dimensions of an oil container are 25, 25 and 15 cm. Find the cost of the iron sheet for making these 20 containers at the rate of Rs 20 per \[{{m}^{2}}.\]
(a) Rs 111
(b) Rs113
(c) Rs 110
(d) All of these
(e) None of these
Answer: (c)
Explanation
Length of container (L) = 25, Breadth of container (b) = 25, Height (H) = 15
Total surface area of the sheet \[=2(lb+bh+hl)\text{ }c{{m}^{2}}\]
\[=2\left( 25\times 25+25\times 15+15\times 25 \right)\text{ }c{{m}^{2}}\]
\[=2\left( 625+375+375 \right)\text{ }c{{m}^{2}}=2(1375)c{{m}^{2}}=2750\text{ }c{{m}^{2}}\]
The total area of required sheet to make 20 containers \[=(2750\times 20)\text{ }c{{m}^{2}}\] \[=55000\text{ }c{{m}^{2}}\text{ }=5.5000\text{ }{{m}^{2}}\]
Thus, the cost of the sheet at the rate of \[Rs\text{ }20\text{ }per\text{ }{{m}^{2}}\]\[=Rs\left( 20\times 5.5000 \right)\text{ }=Rs\text{ }110.00\]
![]() A barn with a flat roof is rectangular in shape of breadth 10 m length 15 m and height 5 m. It is to be painted inside on the walls and on the ceiling but not on floor. Find the total area to be painted.
A barn with a flat roof is rectangular in shape of breadth 10 m length 15 m and height 5 m. It is to be painted inside on the walls and on the ceiling but not on floor. Find the total area to be painted.
(a) \[400{{m}^{2}}\]
(b) \[300{{m}^{2}}\]
(c) \[1200{{m}^{2}}~~\]
(d) All of these
(e) None of these
Answer: (a)
Explanation
Area of walls floor \[=2(l+b)\times h\] Area of ceiling\[=l\times b=10\times 15=150\text{ }{{m}^{2}}\] Total area to be painted \[=250\text{ }{{m}^{2}}+150\text{ }{{m}^{2}}=400\text{ }{{m}^{2}}\]
![]() The floor of a rectangular hall has a perimetre of 250 m. If its height is 6 m. Find the cost of painting of its four walls at the rate of Rs 20 per \[{{m}^{2}}\].
The floor of a rectangular hall has a perimetre of 250 m. If its height is 6 m. Find the cost of painting of its four walls at the rate of Rs 20 per \[{{m}^{2}}\].
(a) Rs 3400
(b) Rs 30000
(c) Rs 12000
(d) All of these
(e) None of these
Answer: (b)
Explanation
Area of the walls floor \[=2\left( l+b \right)\times h\]= Perimetre\[\times h\] \[=250\text{ }m\times 6\text{ }m\text{ }=1500\text{ }{{m}^{2}}\] Cost of painting \[=Rs\left( 1500\text{ }\times 20 \right)=\text{Rs }30,000\]
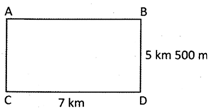
![]() A colony is to be built on a rectangular plot of land. The length of the plot is 7 km and breadth is 5 km 500 m. Find the area of the plot in square kilometers.
A colony is to be built on a rectangular plot of land. The length of the plot is 7 km and breadth is 5 km 500 m. Find the area of the plot in square kilometers.
(a) \[38.5k{{m}^{2}}\]
(b) 68.3\[k{{m}^{2}}\]
(c) \[35.2k{{m}^{2}}\]
(d) All of these
(e) None of these
Answer: (a)
Explanation
The length of the plot = 7 km
The breadth of the plot = 5 km 500 m = 5.5 km
The area of rectangular plot = length \[\times \] breadth
Area of the plot = 7 km \[\times \] 5.5 km = 7 x 5.5 sq km = 38.5 sq km
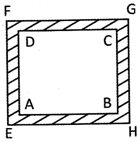
![]() A square lawn is surrounded by a path of 4 m wide. If the area of the path is 320 square metre, find the area of the lawn.
A square lawn is surrounded by a path of 4 m wide. If the area of the path is 320 square metre, find the area of the lawn.
(a) \[385{{m}^{2}}\]
(b) \[~256{{m}^{2}}\]
(c) \[352{{m}^{2}}\]
(d) All of these
(e) None of these
Answer: (b)
Explanation
Let the square ABCD represents the square lawn. The path 4 cm wide around is shown by the shaded portion. Let the side of the square lawn, (Square ABCD) is x m
Area of the square lawn \[=\text{ }{{x}^{2}}\text{ }m\]
Side of the lawn with path \[=\left( x+4+4 \right)\text{ }m\]
Area of the lawn including path \[={{(x+8)}^{2}}\text{ }{{m}^{2}}\] \[=({{x}^{2}}+16x+64)m\]
Area of the path \[~=\text{(}{{x}^{2}}+16x+64\text{)}-{{x}^{2}}\] Or\[({{x}^{2}}+16x+64)-{{x}^{2}}=320\] \[=16x+64\text{ }=320\]
\[=16x=320-64=256\]
\[=x=\frac{256}{16}=16\,\,m\] The area of the square lawn \[=16\times 16=256\text{ }{{m}^{2}}\]
![]() Find the distance covered by a wheel of a bus in 1000 rotations if the diameter of the wheel is 98 cm.
Find the distance covered by a wheel of a bus in 1000 rotations if the diameter of the wheel is 98 cm.
(a) 8634m
(b) 2345m
(c) 3080m
(d) All of these
(e) None of these
Answer: (c)
Explanation
Distance covered by wheel in 1000 rotations \[=1000\times 2\pi r=1000\text{ }\pi d\]
\[=1000\times \frac{22}{7}\times 98\] \[=1000\times 22\times 14\] = 308000 cm = 3080 metre
![]() A rectangular lawn of length 40 m and breadth 25 m is to be surrounded all around by a path which is 2 m wide. Find the area of the path.
A rectangular lawn of length 40 m and breadth 25 m is to be surrounded all around by a path which is 2 m wide. Find the area of the path.
(a) \[276{{m}^{2}}~~\]
(b) \[345{{m}^{2}}\]
(c) \[308{{m}^{2}}~~\]
(d) All of these
(e) None of these
Answer: (a)
Explanation
Area of the path
\[=2\left( 44\times 2 \right)+2\left( 25\times 2 \right)=176+100=276{{m}^{2}}\]
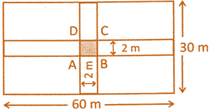
![]() A garden is 60 m by 30 m. It has two paths at the centre as shown in the figure if the width of the path is 2m. How much area is left for gardening?
A garden is 60 m by 30 m. It has two paths at the centre as shown in the figure if the width of the path is 2m. How much area is left for gardening?
(a) \[1441{{m}^{2}}~~~\]
(b) \[~1624{{m}^{2}}\]
(c) \[1328\text{ }{{m}^{2}}~\]
(d) All of these
(e) None of these
Answer: (b)
Explanation
Area for gardening \[=4(14\times 29)=1624{{m}^{2}}\]

![]()
You need to login to perform this action.
You will be redirected in
3 sec
