6th Class Mathematics Fractions Addition Subtraction, Multiplication and Division of Fractions

Addition Subtraction, Multiplication and Division of Fractions  

 

 

Addition of Like Fractions

Addition of like fractions is the addition of its numerator and denominator of the resulting fraction is same as the common denominator.

Like fractions are \[\frac{9}{61},\frac{7}{61},\frac{5}{61},\] therefore, the addition of the fractions \[\text{=}\frac{\text{Additionofnumerators}}{\text{Common denominators }\!\!~\!\!\text{ }}\text{=}\frac{\text{9+7+5}}{\text{61}}\text{=}\frac{\text{21}}{\text{61}}\text{.}\]  

 

 

Find the like fractions from the given fractions and add them:

\[\frac{5}{2},\frac{7}{5},\frac{1}{6},\frac{121}{2},\frac{7}{2}.\]                

(a) \[\frac{133}{2}\]                                       

(b)\[\frac{137}{3}\]

(c) \[\frac{13}{2}\]                          

(d) All of these

(e) None of these  

 

Answer: (a)

Explanation

Like fractions from the given fractions \[=\frac{5}{2},\frac{7}{2},\frac{121}{2}.\] .Their addition \[=\frac{5+7+121}{2}=\frac{133}{2}\]  

 

 

Addition of Unlike Fractions

The following are the steps to perform the addition of unlike fractions:

Step 1:   Find the LCM of denominators of the fractions.

Step 2:   Multiply the numerators and denominators of all the given fractions to their LCM.

Step 3:   Add the numerators and write down the addition over common denominator.

Step 4:    Reduce the resulting fraction into its lowest term if necessary.

Let two unlike fractions are \[\frac{7}{8},\frac{9}{4},\] therefore, LCM of denominators is 8.

Now one fraction has same denominator as the LCM but other has different, so, to make it same as LCM, it should be multiplied by 2, thus the equivalent fraction is\[\frac{9}{4}\times \frac{2}{2}=\frac{18}{8}.\]

Now the addition \[\frac{7}{8},\frac{18}{8}=\frac{7}{8}+\frac{18}{8}=\frac{25}{8}.\]  

 

 

Add the unlike fractions from the given fractions. Choose the correct option for their resulting addition?                

\[\frac{3}{4},\frac{7}{2},\frac{5}{9},\frac{3}{2},\frac{1}{8}.\]                

(a) \[\frac{72}{103}\]                     

(b) \[\frac{103}{72}\]

(c) \[\frac{7}{103}\]                        

(d) All of these

(e) None of these  

 

Answer: (b)

Explanation

\[\frac{3}{4}+\frac{5}{9}+\frac{1}{8}=\frac{54+40+9}{72}=\frac{103}{72}\]  

 

 

Subtraction of Like Fractions

The subtraction of like fractions is same as its addition except that addition isconverted into subtraction.

Let two like fractions are \[\frac{567}{456},\frac{4546}{456},\]

\[\text{Their subtraction}\,text{=}\frac{\text{Subtraction of its numerators}}{\text{ }\!\!~\!\!\text{ Common denominators}}\] \[\frac{4546}{456}-\frac{567}{456}\,text{=}\frac{4546-567}{\text{ }\!\!~\!\!\text{ 456}}=\frac{3979}{456}\]  

 

 

Choose like fractions from the given fractions and find the difference between greatest and smallest fractions: \[\frac{5}{3},\frac{6}{7},\frac{5}{9},\frac{7}{3}.\]                

(a) \[\frac{7}{9}\]                                                            

(b) \[\frac{2}{3}\]                

(c) \[\frac{5}{7}\]                                                            

(d) All of these

(e) None of these  

 

Answer: (b)                

Explanation

Like fractions are \[\frac{7}{3},\frac{5}{3}\] and their difference \[=\frac{7}{3}-\frac{5}{3}=\frac{2}{3}\]  

 

 

Subtraction of Unlike Fractions

Steps to perform the subtraction of unlike fractions:

Step 1:   Find the LCM of denominators of the fractions.

Step 2:   Convert the fractions into its equivalent fractions in such a way that the denominator of every fraction should be equal to their LCM.

Step 3:   Subtract the numerators and write down the subtraction over common denominator. Let two unlike fractions are,\[\frac{9}{7},\frac{8}{5},\] therefore, LCM of their denominators is 35.

Now multiply the fraction by a number in such a way that denominator should be equal to their LCM. Therefore, the equivalent of \[\frac{9}{7}\] is\[\frac{45}{35}\] and equivalent of \[\frac{8}{5}\] is\[\frac{56}{35},\]now their subtraction \[=\frac{56-45}{35}=\frac{11}{35}.\]  

 

 

Find the difference between the fractions \[\frac{11}{35}\]and \[\frac{7}{5}.\]                

(a)\[\frac{37}{35}\]                        

(b) \[\frac{45}{175}\]                

(c) \[\frac{38}{35}\]                        

(d) All of these

(e) None of these  

 

Answer: (c)                

Explanation

\[\frac{7}{5}-\frac{11}{35}=\frac{49-11}{35}=\frac{38}{35}\]  

 

 

Multiplication of Fractions

The following are the steps to perform the multiplication of unlike and like fractions:

Step 1:   Multiply the numerators and denominators.                      

Step 2:   Write the answer into lowest term of the resulting fraction.        

Let us consider the following unlike fractions  \[\frac{7}{9},\frac{5}{17},\] therefore, multiplication of the fractions \[=\frac{9\times 5}{7\times 17}=\frac{45}{119}.\]

Consider the following like fractions \[\frac{6}{19},\frac{4}{19}\]\[\frac{6}{19},\frac{4}{19},\]multiplication of the fractions     \[\text{=}\frac{\text{Product of numerators }\!\!~\!\!\text{  }\!\!~\!\!\text{  }\!\!~\!\!\text{ }}{\text{Product of denominators }\!\!~\!\!\text{ }}=\frac{6\times 4}{19\times 19}=\frac{24}{361}.\]  

 

 

Find the product of the given fractions and reduce the resulting products into its lowest term: \[\frac{4}{13},\frac{5}{12}.\]

(a) \[\frac{5}{41}\]                          

(b) \[\frac{4}{41}\]

(c) \[\frac{5}{39}\]                          

(d) All of these

(e) None of these

 

Answer: (c)                

Explanation

Product of the fractions \[=\frac{4}{13}\times \frac{5}{12}=\frac{4\times 5}{13\times 12}=\frac{20}{156}\]

The HCF of numerator and denominator = 4, therefore, the lowest or reduced term of the resulting product \[=\frac{20\div 4}{156\div 4}=\frac{5}{39}.\]  

 

 

Division of the Fractions

Division of the fractions is multiplication of dividend by reciprocal of divisor.

Let the fractions are,\[\frac{6}{46},\frac{9}{34},\] division of \[\frac{6}{46}\] by \[\frac{9}{34}\] is written as, \[\frac{6}{46}\div \frac{9}{34}\] and division of the fractions \[=\frac{6}{46}\div \frac{9}{34}=\frac{6}{46}\times \frac{34}{9}=\frac{204}{414}.\] The HCF of 204 and 414 is 6 therefore, \[\frac{34}{69}.\]

 

 

Divide the following fractions, if dividend is \[\frac{7}{4}\]and divisor is\[\frac{24}{16}?\]

(a) \[\frac{7}{2}\]                            

(b) \[\frac{7}{6}\]

(c) \[\frac{5}{2}\]                            

(d) All of these (e) None of these   Answer: (b) Explanation \[\frac{7}{4}\div \frac{24}{16}=\frac{7}{4}\times \frac{16}{24}=\frac{7}{6}\]  

 

 

 

 

Add the following fractions: \[\frac{7}{6},\frac{5}{4},\frac{4}{3}?\]                

(a) \[\frac{15}{3}\]                          

(b) \[\frac{15}{4}\]

(c) \[\frac{15}{2}\]                          

(d) All of these  

(e) None of these  

 

Answer: (b)                

Explanation

\[\frac{7}{6}+\frac{5}{4}+\frac{4}{3}=\frac{14+15+16}{12}=\frac{45}{12}=\frac{15}{4}.\]        

 

 

Subtract the following:

\[\frac{56}{6}-\frac{5}{4}.\]

(a) \[\frac{91}{11}\]                       

(b) \[\frac{91}{12}\]

(c) \[\frac{97}{12}\]                        

(d) All of these

(e) None of these                

 

Answer: (c)                

Explanation

\[\frac{56}{6}-\frac{5}{4}=\frac{112-15}{12}=\frac{97}{12}\]  

 

 

Find the product of the following fractions:

\[\frac{4}{3},\frac{5}{7},\frac{3}{2}.\]                

(a) \[\frac{7}{3}\]                            

(b) \[\frac{10}{7}\]                

(c) \[\frac{10}{3}\]                          

(d) All of these                

(e) None of these  

 

Answer: (b)                

Explanation

\[\frac{4}{3}\times \frac{5}{7}\times \frac{3}{2}=\frac{60}{42}=\frac{10}{7}\]  

 

 

Find the division of the following fractions:

\[\frac{8}{9}\div \frac{3}{27}.\]               

(a) 7                                                       

(b) 9

(c) 8                                                      

(d) All of these

(e) None of these  

 

Answer: (c)                

Explanation

\[\frac{8}{9}\div \frac{3}{27}=\frac{8}{9}\times \frac{27}{3}=8\]  

 

 

Simplify the following:

\[\frac{4}{3}+\frac{5}{9}-\frac{3}{2}\times \frac{5}{7}\div \frac{3}{9}.\]

(a)\[\frac{-482}{251}\]                  

(b) 9

(c) \[\frac{-481}{252}\]                 

(d) All of these

(e) None of these

 

Answer: (c)                

Explanation                

\[\frac{3}{4}+\frac{5}{9}-\frac{3}{2}\times \frac{5}{7}\div \frac{3}{9}=\frac{3}{4}+\frac{5}{9}-\frac{45}{14}=\frac{189+140-810}{252}=\frac{-481}{252}\]  

 

 

  Fractions are represented on the number line in the options below. Which one of the following option is correct about the position of fraction \[\frac{2}{5}\] on the number line?

(a)  

(b)

(c)

(d) All of these

(e) None of these  

 

Answer: (a)  

 

 

If numerator of the fraction represent the number of division on the number line then the denominator represent of which one of the following?

(a) First division from origin        

(b) Total number of division

(c) Second division from origin   

(d) All of these

(e) None of these  

 

Answer: (b)  

 

 

How many composite numbers are there between 10 and 30?

(a) 10                                                    

(b) 9

(c) 13                                                    

(d) All of these

(e) None of these             

 

Answer: (c)

Explanation  

 

 

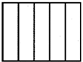
  The composite numbers between 10 to 30 are 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28 = 13. The given figure is divided into 5 equal parts. Which one of the following fraction represents its one part?

 

 

(a) \[\frac{5}{2}\]                            

(b) \[\frac{1}{3}\]

(c) \[\frac{1}{5}\]                            

(d) All of these                 

(e) None of these

 

Answer: (c)

Explanation

The fraction \[\frac{1}{5}\] represents that the figure has been divided into 5 equal parts. Hence, its one part is represented by the fraction \[\frac{1}{5}.\]  

 

Which one of the following options is representing the mixed fraction \[2\frac{3}{5}\]on number line?

(a)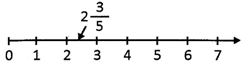

(b)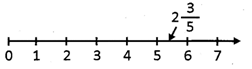                  

(c)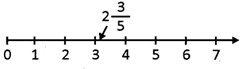

(d) All of these

(e) None of these  

 

Answer: (a)                

Explanation

The position of whole part of mixed fraction \[2\frac{3}{5}\]at 2 and fractional part between 3 and 4. Hence, option (A) is representing the position of mixed fraction \[2\frac{3}{5}\] on the number line.  

 

 

Arrange the given fractions in ascending order:

\[\frac{5}{6},\frac{7}{9},\frac{8}{3}.\]                

(a) \[\frac{5}{6}<\frac{7}{9}<\frac{8}{3}\]                                             

(b) \[\frac{7}{9}>\frac{5}{6}<\frac{8}{3}\]

(c) \[\frac{5}{6}<\frac{8}{3}<\frac{7}{9}\]                             

(d) All of these

(e) None of these  

 

Answer: (b)                

Explanation

LCM of denominators of the fractions is 18. Hence, the equivalent fractions of the given fractions, \[\frac{5}{6},\frac{7}{9},\frac{8}{3}=\frac{15}{18},\frac{14}{18},\frac{48}{18}\] ascending order                

\[=\frac{5}{6}<\frac{5}{6}<\frac{8}{3}.\]  

 

 

Find three equivalent fractions of \[\frac{4}{3}.\]

(a) \[\frac{14}{3},\frac{11}{6},\frac{5}{3}\]                           

(b) \[\frac{12}{3},\frac{10}{6},\frac{6}{7}\]

(c) \[\frac{8}{6},\frac{12}{9},\frac{16}{12}\]  

(d) All of these

(e) None of these                

 

Answer: (c)                

Explanation

\[\frac{4}{3}=\frac{4}{3}\times \frac{2}{2}=\frac{8}{6},\frac{4}{3}\times \frac{3}{3}=\frac{12}{9},\frac{4}{3}\times \frac{4}{4}=\frac{16}{12}.\]                

 

 

Choose the equivalent fraction of \[\frac{7}{2}\] whose denominator is 12 from the following options:

(a) \[\frac{42}{12}\]                                                       

(b) \[\frac{43}{12}\]

(c) \[\frac{44}{12}\]                        

(d) All of these                

(e) None of these  

 

Answer: (a)                

Explanation

\[\frac{7}{2}=\frac{7}{2}\times \frac{6}{6}=\frac{42}{12}.\]  

 

 

  Find the simplest or reduced form of the fraction, \[\frac{24}{3}.\]

(a) 7                                                      

(b) 8            

(c) 9                                                      

(d) All of these

(e) None of these  

 

Answer: (b)          

 

 

• For the better understanding of the fractions the least common multiple should be known.
• Fractions were written without division line in India.
• Every whole number has las the denominator.
• Zero as the numerator is always zero.
• The word fraction comes from latin word fractio.

 

 

• Fraction \[\frac{\text{a}}{\text{b}}\] is proper fraction even if a < b.
• Fraction\[\frac{\text{a}}{\text{b}}\] is improper fraction even if \[a\ge b.\]
• Fractions having the same denominators are called like fraction and those having different denominators are called unlike fractions.
• If HCF of numerator and denominator of the fraction \[\frac{\text{a}}{\text{b}}\] is not other than 1 then the fraction is called in lowest form. If \[\frac{\text{a}}{\text{b}}\text{=}\frac{\text{c}}{\text{d}}\] then ad = be by cross multiplications.