6th Class Mathematics Mensuration Mensuration Basics

MENSURATION BASICS

MENSURATION

•                    The branch of geometry that deals with the measurement of length, area, or volume.

PERIMETER

•                   The length of the sides enclosing the figure is called its perimeter.

AREA

•                   The amount of space in the boundary of plane figure.
•                    Unit of area is square unit.

Some important formula of Mensuration

SQUARE:-

•                     Perimeter of square\[=4\times side=4a\]
•                    Area of square\[={{(side)}^{2}}={{(a)}^{2}}\]
•                    Diagonal of square \[=\sqrt{2}\times \] side

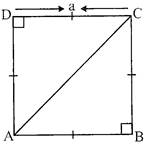
RECTANGLE

•                    Perimeter of rectangle \[=2(l+b)\]
•                   Area of rectangle \[=l\times b\] sq. unit
•                   Diagonal of rectangle \[=\sqrt{{{1}^{2}}+{{b}^{2}}}\]

TRIANGLE

•                    Perimeter of triangle = sum of all side
•                    Area of triangle \[=\frac{1}{2}\times \]base \[\times \]height sq. unit

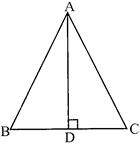
\[=\frac{1}{2}\times AD\times BC\]sq. unit

•                    Area of equilateral triangle \[=\frac{\sqrt{3}}{4}\times {{\left( side \right)}^{2}}\]

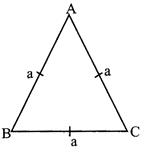
\[=\frac{\sqrt{3}}{4}\times {{\left( a \right)}^{2}}\]sq. unit

CIRCLE

•                     Circumference of circle \[=2\pi r\]
•                     Area of circle\[=\pi {{r}^{2}}\]sq. unit

•                    Area of quadrant \[=\frac{1}{4}\pi {{r}^{2}}\]sq. unit

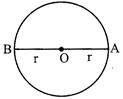
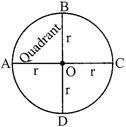
Note\[\to \pi =\frac{22}{7},\,3.14\]

•                   Area of semicircle \[=\frac{1}{2}\pi {{r}^{2}}\] sq. unit

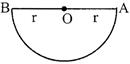
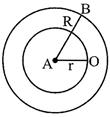
RING

•                    Area of ring \[=\pi \left( {{R}^{2}}-{{r}^{2}} \right)\] sq. unit

Example 1: The area of a rectangle is\[270\,\,c{{m}^{2}}\]. If its length is 30 cm, find its breadth.

Solution: We have

Area of rectangle\[=270\,\,c{{m}^{2}}\]

Length of rectangle \[=30\,\,cm\]

\[\therefore \]Breadth of rectangle\[=\left( \frac{Area}{Length} \right)cm\]

\[=\left( \frac{Area}{Length} \right)cm\]

Example 2: Find the area of shaded region.

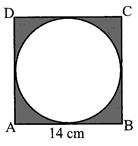
Solution: Area square\[={{(side)}^{2}}\]

\[\Rightarrow \]\[{{(14)}^{2}}=196\,\,c{{m}^{2}}\]

Now, diameter \[=14\,\,cm\]

Radius\[=\frac{14}{2}=7\,\,cm\]

Area\[=\pi {{r}^{2}}=\frac{22}{7}\times 7\times 7=154\,\,c{{m}^{2}}\]

Area of shaded region

\[=196\,\,c{{m}^{2}}-154\,\,c{{m}^{2}}\]

\[=42\,\,c{{m}^{2}}\]

Example 3: Find the area of triangle, whose base and height are 13 cm and 14 cm.

Solution: Area of triangle\[=\frac{1}{2}\times \]base\[\times \]height\[=\frac{1}{2}\times 13\times 14\,\,c{{m}^{2}}\]

\[=91\,\,c{{m}^{2}}\]