Miscellaneous
Category : 6th Class
FACE VALUE
The face value of a number does not change regardless of the place it occupies. Therefore, the face value of a number is the number itself.
For example: 781 face value of 7 = 7.
Face value of 8 = 8, Face value of 1 = 1.
SUCCESSOR
Successor of every number comes just after the number. It is obtained by adding 1 to the given number.
For example: Successor of 28 = 28 + 1 = 29
Successor of 79 = 79 + 1 = 80.
PREDECESSOR
Predecessor of every number comes just before the number.
It is obtained by subtracting 1 from the given number.
For example: Predecessor of 28 = 28 - 1 = 27
Predecessor of 30 = 30 - 1 = 29
ADDITION OF INTEGERS
Examples: Add:
+36 + 27
+ 36
+ 27
+ 63
Examples: Add:
+36 - 27
+36
-27
+ 9
PROPERTIES OF ADDITION OF INTEGERS
Examples: (i) 4 + 3 = 7, which is an integer
(ii) 4 + (-3) = 1, which is an integer
(iii) - 4 + 3 = - 1, which is an integer
(iv) - 4 + (-3) = -7, which is an integer
x + y = y+ x
Examples:
(i) – 7 + 8 = 1 and 8 + (-7) = 1
\[\therefore \] -7 + 8 = 8 + (-7)
(ii) (-5) + (-8) = -13 and (-8) + (-5) = -13
\[\therefore \] (-5) + (-8) = (-8) + (-5)
(x + y) + z = x + (y + z)
Example: {(-5) + (- 6)} + 7 = -11 + 7 = -4
(-5) + {(- 6) + 7} = -5 + 1 = - 4
\[\therefore \] {(-5) + (- 6)} + 7 = - 5 + {(-6) + 7}
SUBTRACTION OF INTEGERS
For any integers x and y, we define.
(i) x - y = x + (additive inverse of y)\[=x+(-y)\]
(ii) x - (- y) = x + {additive inverse of (- y)} = x + y
PROPERTIES OF SUBTRACTION OF INTEGERS
Examples:
(i) 3 - 5 = - 2, which is an integer
(ii) (-3) - 6 = - 9, which is an integer
Examples:
(i) Consider the integers 2 and 4, we have
(2 - 4) = 2 + (- 4) = -2 and (4 - 2) = 4 + (-2) = 2
\[\therefore \,\,(2-4)\ne (4-2)\].
(ii) Consider the integers (-5) and 3 we have
(-5) -3 = (-5) + (- 3) = -8 and 3 - (-5) = 8
\[\therefore \,\,(-5)-3\ne -3-(-5)\]
{4 - (-5)} - (-6) = (4 + 5) - (- 6) = 9 - (- 6) = 9 + 6 = 15
4 - {(-5) - (-6)} = 4 - {(-5) + 6} = 4 - 1 = 3
{4 - (-5)} - (-6) ^ 4 - {(-5) - (- 6)}
MULTIPLICATION OF INTEGERS
Rule 1: To find the product of two integers with unlike sign, first get their product regardless to their signs, then give minus sign to the product.
Examples:
\[(-40)\times 9\]
= - 360
Rule 2: To find the product of two integers with like signs, first find their product regardless to their signs then put plus sign to product.
Examples:
\[3\times 5\]
= + 15
PROPERTIES OF MULTIPLICATION OF INTEGERS
Examples:
(i) \[3\times 2=6\], which is an integer
(ii) \[(-3)\,\times 2=-6,\] which is an integer
\[(x\times y)=(y\,\times x)\]
Examples:
(i) \[2\times (-6)=-12\] and \[(-6)\times 2=-12\]
\[\therefore \,\,2\times (-6)=(-6)\times 2\]
(ii) \[(-3)\times (-7)\,=21\] and \[(-7)\times (-3)\,=21\]
\[\therefore \,(-3)\,\times (-7)\,=(-7)\,\times (-3)\]
Examples:
Consider the integers 3, (- 4) and (-5), we have
\[\{3\times (-4)\}\times (-5)\,=-12\times (-5)=60\]
and \[3\times \{(-4)\times (-5)\}=3\times 20=60\]
\[\therefore \] \[\{3\times (-4)\}\,\times (-5)\,=3\times \,\{(-4)\times (-5)\}\]
DIVISION OF INTEGERS
Rule 1: To find the division of two integers with unlike sign, first get their quotient regardless to their signs, then give minus sign to the product.
Example:
\[-74\div 2\]
\[=\frac{-74}{2}\]
= - 37
Rule 2: To find the division of two integers with like signs, first find their product regardless to their signs then put plus sign to quotient.
Example:
\[48\pm 6\]
\[=\frac{48}{6}\]
= 8
PROPERTIES OF DIVISION OF INTEGERS:
Example:
(i) 12 and 5 are both integer but (12 - 5) is not an integer.
(ii) (-12) and 5 are both integer. But [(-12) - 5)] is not an integer.
Examples:
(i) \[10\div 10=1\]
(ii) \[(-5)\div (-5)=1\]
Examples:
(i) \[5\div 1=5\]
(ii) \[(-5)\div 1=(-5)\]
Examples:
(i) \[0\div 9=0\]
(ii) \[0\div (-9)=0\]
BODMAS RULE
When a single expression contains many mathematical operations then BODMAS rules are used for multiplication of the expression the word BODMAS has been arranged according to the priority of the operations.
BODMAS STANDS FOR
B stands for Bracket
O stands for of
D stands for Division
M stands for Multiplication
A stands for Addition
S stands for Subtraction
BRACKET
Sometimes in complex expressions, we require a set of operations to be performed prior to the others. Here we make use of brackets. Brackets which are commonly used are:
Bracket Name
() Parentheses or common bracket
{} Brace or curly bracket
[ ] Square on box bracket
ELIMINATION OF BRACKETS
The solution of the expression is obtained by eliminating the brackets.
For example:
Steps to simplify the expression \[[\{2+4)\times 5\}-1]:\]
1st step: Eliminate the common bracket by adding 2 and \[4=[\{6\times 5\}-1]\]
2nd step: Eliminate the curly bracket by multiplying 6 and 5 = [30 - 1]
3rd step: Eliminate the box bracket by subtracting 30 and 1 = 29
The solution of the given expression is 29.
DIVISION OF ALGEBRIC EXPRESSION
To divide one polynomial to other (i) keep the polynomials which is to be divided in division form (ii) then divide first term of dividend by first term of divisor and write quotient (iii) then write the product of quotient x divisor, below the divident and subtract it from dividend (iv) repeat this process until the degree of remainder becomes less than divisor.
For example: \[2{{x}^{2}}+3x+1\] by \[(x+1)\]
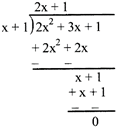
Quotient of the division \[=2x+1\]
MULTIPLICATION OF FRACTIONS
To multiply like or unlike fractions, we should first multiply the numerators and denominators and then, write the answer into lowest term of the resulting fraction.
For example:
To multiply \[\frac{8}{3}\] and \[\frac{24}{5}\]
Multiplication of the fractions
\[=\frac{\text{Product}\,\text{of}\,\text{numerators}}{\text{Product}\,\text{of}\,\text{denominators}}\]
\[=\frac{8\times 24}{3\times 5}\,=\frac{192}{15}\]
The HCF of 192 and 15 is 3, therefore, \[\frac{192\div 3}{15\div 3}\,=\frac{64}{5}\]
DIVISION OF FRACTIONS
To divide the fractions, we should first multiply the dividend by reciprocal of divisor and then, write the answer into lowest term of the resulting fraction.
For example:
To divide \[\frac{75}{6}\] by \[\frac{18}{5}\]
Division of fractions \[=\frac{75}{6}\div \frac{18}{5}\,=\frac{75}{6}\,\times \frac{5}{18}\,=\frac{375}{108}\]
The HCF of 375 and 108 is 3 therefore,
\[=\frac{375\div 3}{108\div 3}\,=\frac{125}{36}\]
MULTIPLICATION OF DEC IMALS
Step (i) Multiply the given decimals by omitting decimal point.
Step (ii) Put the decimal point in the result by counting total number of decimal places for both the decimals.
For example:
The multiply 16.24 and 41.16
1624
x 4116
________
6684384
Now, the total decimal places in the given decimals = 4
So, resulting product = 668.4384
DIVISION OF DECIMALS
Step (i) Decimal point of the divisor is moved to right until it becomes a whole number.
Step (ii) Decimal point of the dividend is moved to right as same as the number of places have been moved in divisor.
Step (iii) Multiply both divisor and dividend by a number to get whole number of necessary.
Step (iv) Put decimal point in the quotient by counting total number of decimal places for both dividend and divisor
For example:
Division of 467.2 by 2.4
\[=\frac{467.2}{2.4}=\frac{4672}{24}\times \frac{10}{10}\,=194.6\]
PARALLELOGRAM
Perimeter of parallelogram ABCD = 2 (Sum of two adjacent sides)
= 2(AB + BC)
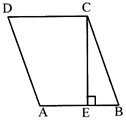
Area of parallelogram ABCD = Base x Height
= AB x CE
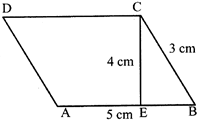
For example:
For the adjoining parallelogram find:
(i) the perimeter
(ii) the area
Solution:
Perimeter = 2 (AB + BC)
= 2 (5 + 3) = 16 cm
Area \[=AB\times CE\]
\[=5\times 4=20\,c{{m}^{2}}\]
You need to login to perform this action.
You will be redirected in
3 sec
