6th Class Mathematics Knowing our Numbers Number System

NUMBER SYSTEM

 

FUNDAMENTALS                     

•                   Digits: for representing any number we use ten symbols

0, 1, 2, 3,4,5,6,7,8,9

All the other numbers are written using 10 symbols.

Example: 2, 3, 4, 5 etc.

•                  Numeral: A group of digits representing a number is called a numeral.

Example: 243, 67842, 546380, etc. are numerals.

•                  Notation: The system of expressing a number in figure or digits is called notation.
•                  Numeration: The logic of representing a number in words is called numeration.

 

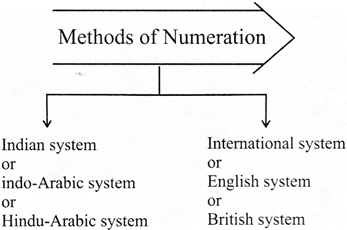
                                               \[\Rightarrow \]    Let us see the chart of Indian system and understand about Indian system.

Periods	Crores		Lakhs		Thousands		Ones
Places	Ten Crores 100000000	Crores 10000000	Ten  Lakhs 1000000	Lakhs 100000	Ten Thousands 10000	Thousand 1000	Hundreds 100	Tens 10	Units 1

 

Example: 67842678 = Six Crore Seventy Eight Lakhs Forty Two Thousand Six Hundred Seventy Eight

 

                                            \[\Rightarrow \]    Let us see the chart of International system and understand about International system.

Periods	Millions			Thousands			Ones
Places	Hundred Millions 100000000	Ten Millions 10000000	Millions 1000000	Hundred Thousand 100000	Ten Thousands 10000	Thousand 1000	Hundreds 100	Tens 10	Units 1

 

Example:     1234567 = One Million Two Hundred Thirty Four Thousand Five Hundred Sixty Seven.

•                    Inserting Commas

A comma is inserted after each period in Hindu-Arabic system as well as British system.

 

Example:

1.            Six Crore Seventy Eight Lakhs Forty Two Thousand Six Hundred Seventy Eight.

6, 78, 42, 678

2.            One Million Two Hundred Thirty Four Thousand Five Hundred Sixty Seven.

1, 234, 567

 

Place value and Face value

•                 In the Hindu-Arabic system of numeration, each digit of a number has a place value and a face value. The place value of a figure or digit depends on its position, since the face value does not depend on its position.

 

Example: Eighty two thousand four hundred seventy two, that is 82472.

The face value of 2 is 2. Similarly the face value of 7 is 7 and 4, 2 and 8 are 4, 2 and 8 respectively.

 

PLACE VALUE:

2 has the place value \[2\times 1=2\] (ones place)

7 has the place value \[7\times 10=70\] (Tens place)

4 has the place value \[4\times 100=400\] (Hundreds place)

2 has the place value \[2\times 1000=2000\] (Thousands place)

8 has the place value \[8\times 10000=80000\] (Ten Thousands place)

 

Note: Place value of a digit = (face value) \[\times \] (value of place).

 

ROMAN NUMBER

•                 Roman numerals are a system of numerical notations used by the Romans. They are an additive (and subtractive) system in which letters are used to denote certain "base" numbers, and arbitrary numbers are then denoted using combinations of symbols.

                                 \[\Rightarrow \]    Roman symbols and their corresponding Indo-Arabic Numerals.

Roman numerals	I	V	X	L	C	D	M
Indo-Arabic Numerals	1	5	10	50	100	500	1000

 

Roman Numerals Fundamental Rules

•                    If a symbol in roman numeral system is repeated, its value is added as many times as it appears.

 

Example:          \[III=1+1+1=3\]

\[XXX=10+10+10=30\]

\[CC=100+100=200\]

\[III=1000+1000+1000=3000.\]

It may "be note that no numerals can be repeated more than 3 times. Repetition is allowed only for symbols I, X and C.

Estimation           

•                    Estimation means finding a number that is close enough to the right answer.
•                    Rounding off a number to the nearest tens, hundreds and thousands.

 

Examples:

1.            54 = 50 (to the nearest tens)

2.            543 = 500 (to the nearest hundreds)

3.            5678 = 6000 (to the nearest thousand)

 

INTEGERS

•                  The set of whole numbers together with negatives of natural numbers is called integers.
•                  It is denoted by I or Z.

\[\therefore \]\[Z=\{---,-4,-3,-2,-1,0,1,2,3,4,----\}\]

•                 The numbers \[1,\,\,2,\,\,3,\,\,4,\,\,5\text{ }---------\] etc. are known as positive integers.
•                 The numbers\[-1,\,\,-2,\,\,-3,\,\,-4,\,\,-5,\,\,-6,\,\,-7,\]------- etc. are known as negative integers.
•                 0 is an integer which is neither positive nor negative.

 

NUMBER LINE

•                  The integers are represented by points at equal intervals on a straight line called number line.
•                   Number line is also known as Real line.

•                   On the number line, 0 lies on the left of positive integer. Therefore all positive integers are greater than 0.
•         On the number line, 0 lies on the right of negative integer. Therefore 0 is greater than every negative integer.
•                  On the number line, every negative integer lies on the left of every positive integer.
•                  Therefore every negative integer is less than positive integer.

 

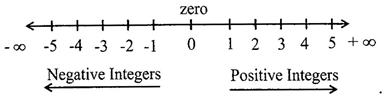
Example:   \[-5<\text{ }5,-7<\text{ }1,-9<\text{ }3\]

Note: A number line drawn vertically, helps to know the heights above the and below the sea levels which are denoted by positive and negative signs respectively.

 

Absolute value of an integer

•                 The absolute value of an integer is the numerical value of the integer regardless of its sign. The symbol is used to represent the absolute value of an integer.

 

Example: \[|+5|=5,\,\,|-5|=5,\,\,|0|=0\]

If x represents an integer then,

\[|x|=x,\] if \[x\] is positive or zero

\[=-x\] if \[x\] is negative.

 

 

Fundamental Operations on Integers

 

Addition of two Integers:

Example 1:   \[(-2)+(-1)=-3.\]

               

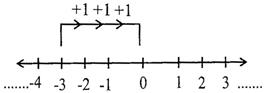
We observe from the number line that \[(-2)+(-1)\]means '2' units to the left of '0' and '1' units to the left of \[(-1)\] gives 3 units to left of zero. i.e.\[(-2)+(-1)=-3.\]

 

Example 2: \[(-2)+(1)=-1.\]

               

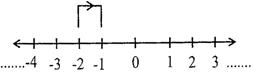
We observe from the number line that \[\{(-2)+1\}\]means '2' units to the left of zero and '1' unit right of \['-2'\] gives '1' unit left of zero. i.e. \[(-2)+1=-1.\]

 

Subtraction of Integers

Example 1:  \[7-2=5\]here, 5 gets the sign of 7 and on number line it is represented as follows.

           

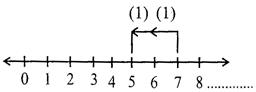
i.e. \[7-2\]means 2 unit to left of 7.

 

Example 2:   \[-7-(-2)=-7+2=-5\]

               

ie. \[-7-(-2)\] follows the rule of sign and becomes \[-7+2\] which is equal to 2 unit to the right of \[-7\] on number line.

 

Example 3: \[-7-(2)=-9\]

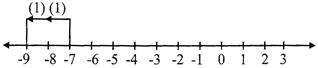
i.e., \[-7-2\]means 2 units to the left of\[-7\]and gives\[-9\].

 

 Things to Remember

 

\[-\times -=+\]	\[-\,2\times -2=+\,4\]	Sum of consecutive natural numbers \[=\frac{n\,(n+1)}{2}\] e.g, 1 + 2 + 3 + 4 + ???. + 50
\[-\times +=-\]	\[-\,3\times 1=-\,3\]
\[+\times -=-\]	\[4\times -2=-\,8\].
\[+\times +=+\]	\[2\times 6=12\]	Solution: \[\frac{50\,(51)}{2}=25\times 51=1275\]