Number System
Category : 6th Class
Number System
Learning Objective
Number System
A system of naming or representing numbers.
Number
A number is a mathematical object which is used to count, label and measure,
Example
1, 5, 19, 325
Main Type
Natural numbers/whole-numbers, integers, rational numbers, irrational numbers, real numbers.
Natural Numbers
Counting numbers 1, 2, 3, 4, 5, 6... are called natural numbers. These numbers are also referred to as the positive integers.
Properties
Whole Numbers
The natural numbers along with zero form the collection of whole numbers.
Example
0, 1, 2, 3, 4, 5, 6 ....
Properties
Factors
A factor of a number is an exact divisor of that number.
Example 1
Factors of \[4=1,\,2,\,4\]
Example 2
Factors of \[15=1,\,3,\,5,\,15\]
Properties
Multiple
A multiple of any natural number is a number formed by multiplying that number by any whole number or a multiple is the product of any quantity and an integer or a number is said to be multiple of any of its factors.
Example 1
First three multiple of 4 are \[4\times 1= 4,4\times 2 = 8\] and \[4\times 3 =12\]
Example 2
First three multiple of 19 are \[19\times 1=19,19\times 2=38\] and \[19\times 3=57\]
Properties
Prime Numbers
The numbers which have exactly two factors, 1 and the number itself, are called prime numbers.
Example
2, 3, 5, 7 etc. are example of prime numbers.
Properties
Co-primes: Two natural numbers which have only the common factor 1 are called co-primes.
Example
Some examples of pairs of co "primes are \[\left( 2,3 \right),\left( 5,7 \right),\left( 8,13 \right),\left( 17,26 \right),\left( 29,33 \right).\]
Twin-primes: Prime numbers that differ by 2 are called twin-primes.
Example
Some examples of pairs of twin-primes are \[\left( 3,5 \right),\left( 5,7 \right),\left( 11,13 \right),\left( 17,19 \right)\left( 29,31 \right).\]
Prime triplet: A prime triplet is a set of three prime numbers of the form \[\left( P,P+2+P+6 \right)\] or\[~\left( p,p+4,P+6 \right).\]
Example
Some examples of prime triplets are \[\left( 5,7,11 \right),\left( 7,11,13 \right),\left( 11,13,17 \right),\left( 13,17,19 \right),\left( 17,19,23 \right),\left( 37,41,43 \right).\]
Composite Number
Numbers having more than two factors are called composite numbers.
Example
4, 6, 8, 9 are example of composite numbers.
Properties:
Test for divisibility of numbers
Example: \[20,40,50,100,200,260\] all are divisible by 10
Example: 15, 20, 25, 30 are divisible by 5.
Example: 6, 24, 20, 34,102 are divisible by 2.
Example: 9, 96,102, 201, 216 are divisible by 3.
Example: 12, 24, 60, 36 are divisible by both 2 and 3 and also by 6.
Example: 324, 428, 520, 672 are divisible by 4
Example: 1000, 1728, 13824, 8184 are divisible by 8
Example: 981, 729,108, 21456 are divisible by 9
Example: 132, 1452, 7172, 2277 are divisible by 11
HCF (highest common factor)
The HCF of two or more numbers is the greatest number which divides each number exactly.
Example
HCF of 9 and 12 is 3 because 3 is the highest common factor among all the common factors of 9 and 12.
Properties
LCM (lowest common multiple)
The LCM of two or more given numbers is the lowest (or smallest) of their common multiples.
Example
LCM of 18 and 24 is 72 because 72 is the smallest common multiple among all the common multiples of 18 and 24.
Properties
Integers
It includes the counting number \[\left( 1,1,~3,4.... \right)\], zero (0) and the negative of counting number \[\left( -1,-2,-3,-4... \right)\] So we can denote integers like this \[\left( ...-4,-3,-1,-1,0,1,2,3,4... \right).\] Denotation of integers on the number line has been shown below.
![]()
Properties
Example
Write all the integers between -3 and 4
Explanation: The integers between -3 and 4 are \[-2,-1,0,1,2\] and 3.
![]()
Fractions
A fraction is a number which represents a part of a whole. The whole may be a single object or a group of objects. A fraction is written in the form a/b where a is called numerator of the fraction and b is called denominator of the fraction.
Example
\[\frac{5}{7},\frac{9}{8}\] and \[\frac{11}{13}\] are examples of fractions.
Proper fraction: A fraction whose numerator is smaller than its denominator is called a proper fraction.
Example
\[\frac{5}{7},\frac{5}{4}\] and \[\frac{54}{59}\] are examples of proper fractions.
Improper fraction: A fraction whose numerator is greater than its denominator is called an improper fraction.
Example
\[\frac{9}{8},\frac{15}{13}\] and \[\frac{21}{19}\] are examples of improper tractions.
Mixed fraction: A combination of a whole number and a proper fraction is called a mixed fraction.
Example
\[5\frac{1}{3},2\frac{1}{2}\] and \[3\frac{1}{2}\]are examples of mixed fractions.
Equivalent fraction: Fractions having same value are called equivalent tractions.
Example
\[\frac{4}{5},\frac{8}{10}\] and \[\frac{16}{20}\]are examples of equivalent fractions.
Like fractions: The fractions having same denominators are called like fractions.
Example
\[\frac{4}{5},\frac{8}{10}\] and \[\frac{6}{7}\]are examples of like fractions.
Unlike fractions: The fractions having different denominators are called unlike fractions,
Example
\[\frac{2}{3},\frac{4}{5}\] and \[\frac{6}{7}\] are examples of unlike fractions.
Decimals
The numbers which use a decimal point followed by one or more digits are called decimal numbers.
Example
\[4.25,3.2,0.698\] are examples of decimal numbers.
Properties
Commonly Asked Questions
Which one of the following options is correct?
(a) \[\left( \frac{4}{3}\div 1 \right)-\frac{4}{3}=1\] (b) \[\left( \frac{4}{3}\div 1 \right)-\frac{4}{3}=0-1\]
(c) \[\left( \frac{4}{3}\div 1 \right)-\frac{4}{3}=0\] (d) All of these
(e) None of these
Answer (c)
Explanation: \[\left( \frac{4}{3}\div 1 \right)-\frac{4}{3}=\frac{4}{3}-\frac{4}{3}=0\]
Simplify: \[\mathbf{45+3\times 2}\,\mathbf{of}\,\mathbf{5-(16+4)-8\div 4}\]
(a) 55 (b) 43
(c) 53 (d) Both (a) and (c)
(e) None of these
Answer (c)
Explanation: \[45+3\times 2\text{ }of\,5-\left( 16+4 \right)-8\div 4\]
\[=45+3\times 2\text{ }of\text{ }5-20-8\div 4\] [Bracket removed]
\[=45+3\times 2\text{ }of\text{ }5-20-2\] [Operation of division \[8\div 4=2\]]
\[=45+30-20-2\] [Operation of multiplication \[3\times 2\times 5=30\]]
\[=75-20-2\] [Operation of addition \[45+30=75\]]
\[=75-22=53\] [Operation of subtraction].
In the following picture, some parts of picture are shaded but some are not. What part of the picture is unshaded?
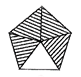
(a) \[\frac{2}{5}\] (b) \[\frac{1}{5}\]
(c) \[\frac{3}{5}\] (d) All of these
(e) None of these
Answer (b)
Explanation: One part of the picture is not shaded but 4 parts are shaded.
Find the product of decimals 234.567 and 123.7.
(a) 29016.9372 (b) 29015.9373
(c) 29016.1853 (d) 29015.9379
(e) All of these
Answer: (d)
Explanation: \[234.569\times 123.7=29015.9379.\]
Write the shortest form of the following: \[\mathbf{4000+500+8+0+}\frac{\mathbf{7}}{\mathbf{10}}\mathbf{+}\frac{\mathbf{6}}{\mathbf{1000}}\mathbf{.}\]
(a) 4508.706 (b) 4507.705
(c) 4509.707 (d) All of these
(e) None of these
Answer (a)
Explanation: \[4000+500+8+0+\frac{7}{10}+\frac{6}{1000}=4508.706.\]
You need to login to perform this action.
You will be redirected in
3 sec
