Applied Mathematics
Category : 7th Class
Applied Mathematics
In this chapter, we will learn about sets, operations on sets, venn diagrams and other real life word problems on average and annual installments.
Empty Set (or null set)
A set containing no element is called an empty set. It is represented by {} or \[\phi \] (read as phi). eg. The set of all whole numbers than 0.
Singleton Set
A set containing a single element is called a singleton set. eg. The set of all even prime numbers.
Disjoint Sets
Two set A and B are called to be disjoint, if they have no elements in common.
e.g. Sets A {2, 4, 6, 8, 4, 10, 12} and B = {1, 3, 5, 7, 9, 11}
\[\Rightarrow A\cap B=\phi \] \[\Rightarrow \]A and B are disjoint sets.
Subset and Superset
For any two sets A and B if every element of A is an element of B, then A is called the subset of B and B is called superset of A.
\[\Rightarrow A\subseteq B\,\,\,or\,\,\,B\supseteq A \]
Here the symbol \['\subset '\] stands for ?is a subset of?. eg. Set of all primes is a subset of the set of all whole numbers.
Note: Empty set is a subset of every set.
The number of subsets of a set A having n elements is 2n.
Every set is a subset of itself i.e. \[A\cap A\,\,\,and\,\,\,B\subset B\].
If A = {3, 4, 5} and B = {1, 3, 4, 6, 5} then which one of the following in correct?
(a) \[A\subset B\] (b) \[B\subset A\]
(c) \[A=B\] (d) either (b) or (c)
(e) None of these
Ans. (a)
Explanation: Since, all the elements of set A are contained in sets.
A is a subset of B and but B is not a subset of A. So\[\,\,\,\,\,A\subset B\].
Proper Subset
If A and B are two sets, then A is called the proper subset of B if and only if every element in A is also in B and there exists at least one element in B that is not in A.
Thus we can say that set A is not a proper subset of itself.
For example {1, 2} is a subset of {1, 2} but is not a proper subset of {1, 2}
Note: If A is proper subset of B, then it is also a subset of B.
The proper subset {1, 2, 3, 4, 5} is ________
(a) {1, 2, 3, 4,} (b) {1, 2, 3, 4, 5,}
(c) {1, 2, 3, 5, 4, 6} (d) All the above
(e) None of these
Ans. (a)
Explanation: Clearly {1, 2, 3, 4} is a proper subset {1, 2, 3, 4, 5,}
Universal Set
A set which consists of all the sets under discussion is called the universal set and is denoted by ?U?
For example: If A = {a, b, c}, B = {m, l, n} and C = {1, 4, 5} then U can be {a, b, c, m, l, n, 1, 4, 5}
Complement of a Set
The set of all those elements of universal set which are not in set A is known as the complement of the set A. It is denoted by A? and A\[{}^\circ \].
If U is the universal set such that U = {3, 8, 12, 16} and A = {8, 12} then find A?.
(a) {3, 8} (b) {8, 12}
(c) {3, 16} (d) {8, 12, 16}
(e) None of these
Ans. (c)
Operations on Sets
(1) Union of Sets: Let A and B be two sets. Then the union of sets A and B, represented by \[A\cup B\]is the set of all those elements which are either in A or in B or Both A and B i.e. \[A\cup B=\{x:x\in A\,\,or\,x\in B\}\].
Note: (i) \[A\cup U=U\,\,and\,\,A\cup \phi =A\]
(ii) If \[A\subseteq B,\,\,\,then\,\,A\cup B=B\]
(2) Intersection of Sets: Let A and B be two sets: Then the intersection of A and B, represented by \[A\cap B\]
= is the set of all those elements which are in both A and B.
ie. \[A\cap B=\{x:x\in A\,\,or\,x\in B\}\].
Note: (i) \[A\cap U=A\,\,and\,\,A\cap \phi =\phi \]
(ii) \[A\subseteq B,\,\,\,then\,\,A\cap B=A\]
(iii) For two disjoint sets A and B. \[A\cap B=\phi \]
(3) Difference of Sets: Let A and B be two, sets, then the difference \[A-B\] is the set of all those elements which are in A but not in B i.e. \[A-B=\{x:x\in A\,\,or\,x\in B\}\]
Note: (i) \[A-B=B-A,\] then \[A=B\]
(ii) For a set A, \[A'=U-A\]
If A = {1, 3, 4, 5, 7, 9} and B = {2, 4, 6, 8} then which one of the following is incorrect?
(a) \[A\cup B=\]{1, 2, 3, 4, 5, 6, 7, 8, 9} (b) \[A\cap B=\{4\}\]
(c) \[A-B=\{1,\,3,\,5,\,7,\,9\}\] (d) \[B-A=\{2,4,6,8\}\]
(e) None of these
Ans. (d)
Explanation: Clearly \[B-A=\{2,6,8\}\]
Venn Diagrams
The pictorial representation of sets by the means of diagram is called venn diagrams. In venn diagrams, the universal set is usually represented by a rectangular region. The subsets of universal set is represented by the closed region inside the rectangular region. The elements of the sets are shown in the closed regions.
If U = {1, 2, 3, 9, 10, 11, 13}, A = {2, 9, 6, 11} and B = {2, 9, 13, 1} then draw the venn diagram of the given information.
Solution:
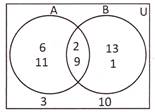
Note:
1. Thus from the above venn diagram,
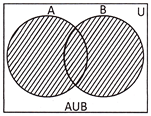
(i) the shaded part represents the set \[A\cup B\]as:
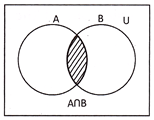
(ii) the shaded part represents the set \[A\cap B\]as:
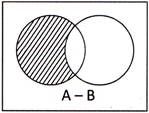
(iii) the shaded part represents the set A ? B, as:
2. Always remember that for any two sets A and B, \[n\,(A\cup B)=n\text{ }\left( A \right)+n\left( B \right)n\text{ }(A\cap B)\]
Average
The average or mean or arithmetic mean of a number of quantities of the same kind is their sum divided by the number.
\[Average\,of\,n\,quantities=\frac{Sum\,of\,Quantities}{n}\]
If the first 10 overs of a cricket game, the run rate was only 4.2. What should be the run rate in the remaining 40 overs to reach the target of 326 runs?
(a) 7.4 (b) 7.1
(c) 7.4 (d) 7.6
(e) None of these
Ans. (b)
Explanation: Required run rate \[=\frac{326-(10\,\times \,4.2)}{40}\,\,=\,\,\frac{284}{40}\,\,=7.1\]
Annual Installment
In our daily life we purchase a product either by paying whole amount at the same time of purchasing or by doing some cash down payment at the time of purchasing and give the remaining amount to the shopkeeper in some monthly or yearly installments. In such a situations the seller gets the installments such that he recovers the interest in several installments. So, if a seller sold a product for t months as selling price = Total installments + interest generated on these installments for remaining period.
For example, if the total loan is for 4 months, the seller gets 3 months, the seller gets 3 months interest on the first installments, 2 months interest on the third installments and no interest on fourth installments.
If installment is asked per year, then general formula installments calculations is
\[x=\frac{100A}{100+rt(t-1)/2'}\]
where A = annual installments, t = time period and r = annual rate of interest.
What equal annual installments will discharge a debt of 5400 due in 58 years at 10%?
(a) 600 (b) 800
(c) 900 (d) 950
(e) None of these
Ans. (c)
Explanation: If each equal annual installments is ` x, then.
Amount of ` x in 4 years + Amount of ` x in 3 years +
Amount of ` x in 2 years + Amount of ` x in a year + ` x = 5400
\[\Rightarrow \left[ \frac{x+x\times 10\times 4}{100} \right]+\left[ \frac{x+x\times 10\times 3}{100} \right]+\left[ \frac{x+x\times 10\times 2}{100} \right]+\left[ \frac{x+x\times 20\times 1}{100} \right]+x=5400\]
\[\Rightarrow \,\,\,5x+\frac{40x+30x+20x+10x}{100}=5400\]
\[\Rightarrow \,\,\,5x+x=5400\,\,\,\,\,\Rightarrow \,\,6x=5400\,\,\,\Rightarrow \,\,\,x=\,\,900\]
Alternate Method
Annual installment \[=\frac{100A}{100t+\frac{rt(t-1)}{2}}\]
Where A = amount, t = time period, r= rate of interest annually.
\[\therefore \,\,\,\,\,Annual\,installment\,\,=\,\,\frac{100\times 5400}{100\times 5+\frac{10\times 5\times 4}{2}}=\frac{5400\times 100}{500+100}\]
\[=\,\,\frac{5400\times 100}{600}=Rs.\,900\]
A sum of 6840 is borrowed at 5% simple interest and is paid back in 4 equal annual installments. What is the amount of each installment?
(a) Rs. 1608.60 (b) Rs. 1908.84
(c) Rs. 2000 (d) Rs. 2200
(e) None of these
Ans. (b)
Explanation: Here, we have, \[A\text{ }=\text{ }P\text{ }+\text{ }S.I.\text{ }=\text{ Rs}\text{.}\,\,6840\text{ }+\text{ }6840\times \frac{5\times 4}{100}\]
\[=Rs.\,\,6840+1368=Rs.\,8208\]
\[\therefore \,\,\,\,Annual\,installment=\frac{100\times 8208}{100\times 4+\frac{5\times 4\times 3}{2}}\]
\[=\,\,\,\frac{8208\times 100}{400+30}\,\,=\,\,1908.84\]
You need to login to perform this action.
You will be redirected in
3 sec
