Congruence of Triangles
- Two figures having exactly the same shape and size are said to be congruent.
- Two triangles are said to be congruent, if pairs of corresponding sides and corresponding angles are equal.
Note: The symbol\[\cong \]is used for ‘is Congruent to’ relation.
- Two line segments are congruent, if they have the same length. \[\overline{AB} = \overline{CD}\]is read as line segment \[\overline{AB}\]is congruent to the line segment \[\overline{CD}\]
- Two angles are congruent, if they have the same measure. “\[\angle \]A is congruent to \[\angle \]B” is written symbolically as \[\angle \]A = \[\angle \]B or \[\angle \]A = \[\angle \]B.
- S.S. congruence condition: If the three sides of a triangle are equal to the three corresponding sides of another triangle, then the two triangles are congruent.
e.g. 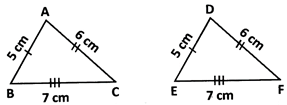
In the given figure, \[\Delta \]ABC =\[\Delta \]DEF by S.S.S. congruence condition.
- A.S. congruence condition: If two sides and the included angle of a triangle are respectively equal to the two corresponding sides and the included angle of another triangle, then the two triangles are congruent.
e.g. 
in the given figure, AABC '= ADEF by S.A.S. congruence condition.
- S.A. congruence condition: If two angles and an included side of one triangle are re- spectively equal to the two corresponding angles and the corresponding included side of another triangle, then the two triangles are congruent.
e.g. 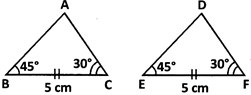
- In the given figure,\[\Delta \]ABC=\[\Delta \]DEF by A.S.A. congruence condition.
- H.S. congruence condition: If the hypotenuse and a side of a right angled triangle are equal to the hypotenuse and the corresponding side of another right-angled triangle then the two triangles are congruent.
e.g.
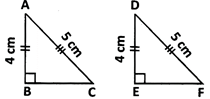
In the given figure,\[\Delta \]ABC\[\cong \]\[\Delta \]DEF by R.H.S. congruence condition.
- In congruent triangles, the congruent angles are opposite to equal sides, and the congruent sides are opposite to equal angles.
- There is no A.A.A. congruence condition for congruence of triangles. Two triangles with equal corresponding angles need not be congruent. In such case, one of the triangles can be an enlarged copy of the other.
- The order of the letters in the names of congruent triangles displays the corresponding relationships.
Thus, if \[\Delta \]ABC\[\cong \]\[\Delta \]EDT, A lies on E, B on D and Con F. Also \[\overline{AB}\]lies along \[\overline{ED}, \overline{BC}\]along \[\overline{DF}\]and \[\overline{AC}\]along\[\overline{EF}\].




