CUBE AND DICE
Category : 7th Class
Learning Objectives
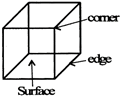
CUBE
INTRODUCTION
Questions on Cube and Dice are an integral part of non-verbal reasoning. Cube is a 3-D figure, having 8 comers (vertices), 6 surfaces and 12 edges. In a cube all the sides (length, breadth and height) are equal.
\[L=B=H.\]
In a cube the number of unit cubes\[={{\left( side \right)}^{3}}\]
Example 1:
A cube of each side 4 cm, has been painted black, red and green on pairs of opposite faces. It is then cut into small cubes of each side 1 cm.
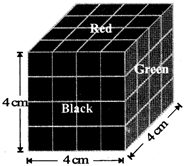
Solve the following questions based on the information given above.
1. How many small cubes will be there?
(a) 16 (b) 64
(c) 24 (d) 8
2. How many small cubes will have three faces painted?
(a) 16 (b) 8
(c) 4 (d) 24
3. How many small cubes will have two faces painted?
(a) 8 (b) 16
(c) 24 (d) None of these
4. How many small cubes will have only one face painted?
(a) 8 (b) 16
(c) 24 (d) None of these
5. How many small cubes will have no face painted?
(a) 8 (b) 16
(c) 24 (d) Nil
6. How many small cubes will have only two faces painted in green and black and all other faces not painted?
(a) 8 (b) 16
(c) 24 (d) None of these
Solutions
1. (b) 64
Total number of small cubes\[=4\times 4\times 4=64\]
2. (b) 8
From the figure it is clear that the small cubes having three faces painted are situated at the comers of the big cube, because at these comers only three faces of the big cube meet.
\[\therefore \] Required number of such cubes = 8
(Because there are 8 comers).
3. (c) 24
From the figure it is clear that to each edge of the big cube 4 small cubes are connected and two out of them are situated at the comers of the big cube which have three faces painted.

Thus, to an edge two small cubes are left which have two faces painted. As the total edges in a cube are 12, the number of cubes with two faces painted\[=12\times 2=24\]
4. (c) 24
The cubes which are painted on one face only are the cubes at the center of each face.
Since there are 6 faces in the big cube and each of the faces of the big cube will have four such small cubes.
Hence, in all there will be 6 x 4 = 24 such small cubes.
5. (a) 8
Number of small cubes which will have no face painted
\[={{(X-2)}^{3}}(\text{Here}\,X=\frac{4}{1}=4)\]
\[{{(4-2)}^{3}}=8.\]
6. (a) 8
There are 4 small cubes in layer II and 4 small cubes in layer III which have two faces painted green and black.
So, required number of such small cubes\[=4+4=8.\]
DICE
INTRODUCTION
Dice is a three-dimensional figure with all of its surfaces numbered. It has six surfaces and they are numbered from 1 to 6. If the surfaces of the dice are unfolded and placed on a plane, the figure of the dice so obtained will look like one of the following figures:
Form 1:
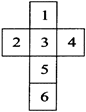
In this case
1 lies opposite to 5.
2 lies opposite to 4.
3 lies opposite to 6.
Form 2:
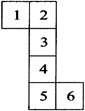
In this case
1 lies opposite to 6.
2 lies opposite to 4.
3 lies opposite to 5.
Form 3:
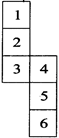
In this case
1 lies opposite to 3.
2 lies opposite to 5.
3 lies opposite to 6.
Form 4:
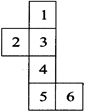
In this case
1 lies opposite to 4.
2 lies opposite to 6.
3 lies opposite to 5.
Example 1:
Select from the alternatives the box that can be formed by folding the sheet shown in figure (X).
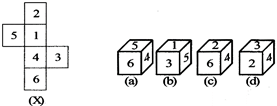
Solution: (a)
![]()
From the unfolded figure of dice, we find that number opposite to 2 is 4, for 5 it is 3 and for 1 it is 6. From this result we can definitely say that fig. (b) and (c) and (d) can't be the answer as number lying on the opposite pair of surfaces are present on the adjacent surfaces. Hence fig (a) is the answer.
Rules of Dice: We can solve questions on dice by following the four rules given below.
Rule 1: Two opposite faces cannot be adjacent to each other.
Example 2:
![]()
Which number will appear on the face opposite to number 4?
Solution:
Faces with four numbers 6, 2, 5 and 3 are adjacent to the face with number 4. Hence, the faces with numbers 6, 2, 5 and 3 cannot be opposite to face with number 4. Therefore the remaining face with number 1 will be opposite to the face with number 4.
Rule 2: If two different positions of a dice are shown and one of the two common faces is in the same position, then the remaining faces will be opposite to each other.
Examples 3:
Two different positions of a dice are shown below.
![]()
Here the faces 5 and 3 are common.
Solution:
The remaining faces are 1 and 4.
Hence the number on the face opposite to face with number 2 is 4.
Rule 3: If in two different positions of the dice, the position of a common face is the same, then each of the opposite faces of the remaining faces will be in the same position.
Example 4:
![]()
Here in both, position of common (3) is same. Therefore, opposite of 5 is 6 and opposite of 4 is 2.
Rule 4: If in two different positions of a dice, the position of the common face is not the same then the face opposite to the common face will be that which is not shown on any face in these two positions.
Example 5:
![]()
It is clear from both positions of the dice, that the face bearing the number 1 is the common face. Face with number 6 is not shown. So Number 6 will be opposite to face with number 1.
You need to login to perform this action.
You will be redirected in
3 sec
