7th Class Mathematics Data Handling Data Handling

 Data Handling

Modern society is information oriented. Every person wants numeric information of different fields of the society like the marks obtained in a particular subject by the students, five year plans etc. Statistics is a branch of mathematics which deals with the process, analyzing and interpreting the data.

Terms Related to Data

•               Data: It is defined as the particular information in numeric form.
•              Primary data: Primary data means the data that have been collected by collector for some purpose.
•              Secondary data: Secondary data is data that have been collected by others and used by other observer.
•              Raw data: It is the original form of the data.                                
•              Frequency: The number of times a particular observation occurs in a data is called frequency.
•             Range: The difference between maximum and minimum value of the observation is called range.
•             Class Interval: The interval in which variates lies is called class interval.
•             Class Mark. \[=\,\,~\frac{1}{2}\,\,\left( lower\text{ }limit\text{ }+\text{ }upper\text{ }limit \right)\]

•             Example:

The runs scored by 11 members of a cricket team are as follows.

            34, 0, 25, 34, 67, 73, 67, 1, 0, 34, 71.

Arrange the above data using tally marks.

•              Example:

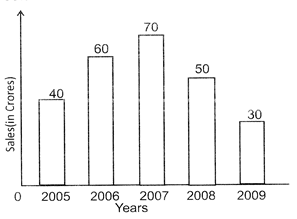
The total sales of a company (in crores) in different years are as follows.

Present the above data in the form of a bar graph.

            Solution:

Mean

Mean is defined as the ratio of sum of observation to total number of observations.

            \[\,Mean=\frac{Sum\,of\,observations}{total\,\,number\,of\,observations}\]

Median

Median of a data refers to the value which lies in the middle of the data with half of the observations above it and the other half below it.

To find the median of a set of observations, we use following steps:

Step 1: Arrange the given data either in ascending or descending order

Step 2: Count the number of observations.

Step 3: If the number of observations is odd, then \[median={{\left( \frac{n+1}{2} \right)}^{th}}\,\,observation\]

Step 4: If the number of observations is even, then \[median=\frac{{{\left( \frac{n}{2} \right)}^{th}}observation\,\,+\,{{\left( \frac{n+1}{2} \right)}^{th}}\,observation}{2}\]

Mode

Mode of a set of observations is the observation that occurs most often.

•               Example:

Find the mean of first five even natural numbers.

            Solution:

            First five even natural numbers are 2, 4, 6, 8, 10

            From the above formula, we get

            \[Mean=\,\,\,\frac{2+4+6+8+10}{5}\,\,=\,\,\,\frac{30}{5}\,\,=\,\,\,6\]