7th Class Mathematics Exponents and Power

EXPONENTS AND POWER

FUNDAMENTALS

•                       Exponential form is nothing but repeated multiplication.

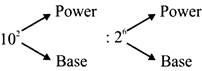
There are two part of an exponent.

Exponent \[\to \] base, Power/ Index

Example:

•                         Base denotes the number to be multiplied and the power denotes the number of times the base is to be multiplied.

\[a\text{ }\times \text{ }a\text{ }\times \text{ }a={{a}^{3}}\] (read as 'a' cubed or 'a' raised to the power 3)

\[a\text{ }\times \text{ }a\text{ }\times \text{ }a\text{ }\times \text{ }a\text{ }\times \text{ }a\text{ }\times \text{ }a={{a}^{6}}\] (read as 'a raised to the power 6 or 6th  power of a)

..............................................................................................................

\[a\text{ }\times \text{ }a\text{ }\times \text{ }a\]....... (n factors) \[=\text{ }{{a}^{n}}\](read as 'a' raise to the power n or nth  power of a)

•                        (a) When a negative number is raised to an even power the value is always positive.

e.g., \[{{(-5)}^{6}}=(-5)\times (-5)\times (-5)\times (-5)\times (-5)\times (-5)=15625\]

(b) When a negative number is raised to an odd power, the value is always negative.

e.g., \[{{(-3)}^{5}}=(-3)\times (-3)\times (-3)\times (-3)\times (-3)=-243\]

Note: (a) \[{{(-1)}^{odd\,\,number}}=-1\]                                  (b) \[{{(-1)}^{even\,\,number}}=+1\]

Elementary question 1:

In \[{{3}^{5}},\]what is the base and power respectively?

Ans.:    Base = 3

Power = 5

Elementary Question 2:

Write 32 in exponent form

Ans.:    \[32=2\times 2\times 2\times 2\times 2={{2}^{5}}~\]     where base = 2              power / Index = 5

•                         Laws of Exponents:

For any non-zero integers 'a' and 'b' and whole numbers 'm' and 'n',

(a)\[a\times a\times a\times ~\]............. \[\times \text{ }a\](m factors) \[={{a}^{m}}~\]

(b) \[{{a}^{m}}\times {{a}^{n}}={{a}^{m+n}}\]

(c) \[\frac{{{a}^{m}}}{{{a}^{n}}}={{a}^{m-n}},\] if m > n; = 1, if m = n ; \[=\frac{1}{{{a}^{n-m}}}\]if m < n

(d) \[{{({{a}^{m}})}^{n}}={{a}^{mn}}\]

(e) \[{{(ab)}^{m}}={{a}^{m}}{{b}^{m}}\]

(f) \[{{\left( \frac{a}{b} \right)}^{m}}=\frac{{{a}^{m}}}{{{b}^{m}}}\]

(g) \[a{}^\circ =1\]

Most of the questions under this chapter are applications of the above formula (a) to (g). Therefore commit them to memory (not ROT memory but learn by applying).

Elementary question 3:

Evaluate:          (i) \[5\times 5\times 5\]     (ii)\[{{5}^{2}}\times {{5}^{3}}\]         (iii) \[\frac{{{5}^{3}}}{{{5}^{2}}}\]                    (iv)\[{{\left( {{5}^{2}} \right)}^{3}}\]  

(v)\[{{\left( 2\times 5 \right)}^{3}}\]        (vi) \[{{\left( \frac{5}{2} \right)}^{2}}\]  (vii) \[5{}^\circ \times 2{}^\circ \times 3{}^\circ \]

Ans.:    (i) \[5\times 5\times 5\](three times)\[={{5}^{3}}=125\]

(ii) \[{{5}^{2}}\times {{5}^{3}}=\text{ }{{5}^{2+3}}=\text{ }{{5}^{5}}=\text{ }3125\]

(iii) \[\frac{{{5}^{3}}}{{{5}^{2}}}={{5}^{3-2}}={{5}^{1}}=5\]

(iv) \[{{({{5}^{2}})}^{3}}={{5}^{2\times 3}}={{5}^{6}}=15625\]

(v) \[{{\left( \frac{5}{2} \right)}^{2}}=\frac{{{5}^{2}}}{{{2}^{2}}}=\frac{25}{4};\]             

(vi) \[{{\left( 2\times 5 \right)}^{3}}={{2}^{3}}\times {{5}^{3}}=8\times 125=1000\]

(vii) \[5{}^\circ \times 2{}^\circ \times 3{}^\circ =1\times 1\times 1=1\]

•                     Any number can be expressed as a decimal number between 1.0 and 10.0 including 1.0 multiplied by a power of 10. Such a form of a number is called its standard form.

For example, standard form of \[63.2=6.32\times 10=6.32\text{ }\times {{10}^{1}}\]

Elementary question 4;

Write 2346 in standard form

Ans.:    \[2.346\times 1000\]so that decimal is after first non-zero digit\[(2)=2.346\times {{10}^{3}}\].