GEOMETRY
Category : 7th Class
Learning Objectives:
LINES AND ANGLES
Angle: An angle is an indication between two rays with the same initial point. Initial point is known as vertex and the two rays are the arms. An angle is represented by the symbol\[\angle \].
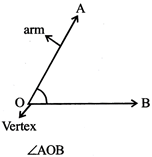
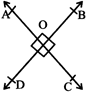
OA & OB are arms O is vertex
SUPPLEMENTARY ANGLES
Two angles are said to be supplementary if the sum of their measures is \[180{}^\circ \] Thus, \[\angle A\] and \[\angle B\] are supplementary if \[\angle A+\angle B=180{}^\circ \]
Example: If \[\angle A=60{}^\circ \] and \[\angle B=120{}^\circ \] then \[\angle A\] and \[\angle B\] are supplementary. Since\[\angle A+\angle B=180{}^\circ \]
COMPLEMENTARY ANGLES
Two angles are said to be complimentary if the sum of their measures is\[90{}^\circ .\]
Example: If \[\angle A=46{}^\circ \] and \[\angle B=44{}^\circ \] then \[\angle A\] and \[\angle B\] are complementary, since \[\angle A+\angle B=90{}^\circ .\]
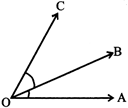
ADJACENT ANGLES
Two angles with same vertex, one common arms and the other arms lying on opposite sides of common arm are called adjacent angles.
In the figure \[\angle BOC\] and \[\angle AOB\] are adjacent angles.
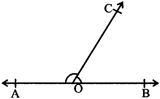
LINEAR PAIR OF ANGLES
Two adjacent angles are said to form linear pair of angles if their non-common arms are two opposite rays,
\[\angle AOC\]and\[\angle BOC\]are two adjacent angles. Their non-common arm OA and OB are two opposite rays.
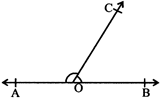
Two important results are obtained from linear pair of angles.
1. The sum of all angles formed on the same side of a line at a given point on the line is \[180{}^\circ \]\[\,\angle AOC+\angle COB=180{}^\circ .\]
The sum of all angles around a point is\[360{}^\circ .\] Thus\[\angle AOB+\angle BOC+\angle COD+\angle DOA=360{}^\circ \]
VERTICALLY OPPOSITE ANGLES
When two lines intersect on a point four angles are formed. Angle 1 is vertically opposite to angle 3. Angle 2 is vertically opposite to angle 4.
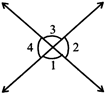
Note: If two lines intersect to each other vertically opposite angles are equal.
PARALLEL LINES
Two lines or line segment in a plane which do not intersect and the perpendicular distance between them remain constant are called parallel lines.
![]()
TRANSVERSAL
A line which intersects two or more lines at distinct points is called a transversal.
ANGLES FORMED WHEN A TRANSVERSAL CUTS TWO PARALLEL LINE
Let two parallel lines\[l\]and\[m\]be cut by a transversal forming angles as shown, we have:
(i) Corresponding angles: \[(\angle 1,\,\,\angle 5),\] \[(\angle 2,\,\,\angle 6),\]\[(\angle 4,\,\,\angle 8),\] \[(\angle 3,\,\,\angle 7)\]are called pairs of corresponding angles which are equal.
(ii) Alternate interior angle: \[(\angle 3,\,\,\angle 5),\] \[(\angle 4,\,\,\angle 6),\] are called alternate interior angles which are equal.
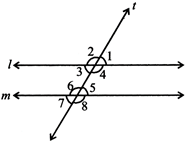
(iii) Alternate exterior angle: \[(\angle 2,\,\,\angle 8),\]\[(\angle 1,\,\,\angle 7)\] are called alternate exterior angle which are equal.
(iv) Consecutive, interior angles: \[(\angle 3,\,\,\angle 6)\] and \[(\angle 4,\,\,\angle 5)\] are called pairs of interior or simply co-interior angles which are supplementary.
Important Results
When a transversal cuts two lines, such that pairs of corresponding angles are equal, then the lines have to be parallel.
When a transversal cuts two lines, such that pairs of alternate interior angles are equal, the lines have to be parallel.
When a transversal cuts two lines, such that pairs of interior angles on the same side of the transversal are supplementary the lines have to be parallel.
TRIANGLE
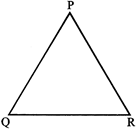
A closed figure formed by joining three non-collinear points is called a triangle
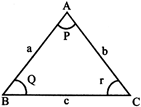
Triangle PQR has
(i) Three vertices P, Q and R.
(ii) Three sides namely, PQ, QR, and PR
(iii) Three angles namely,\[\angle P,\]\[\angle Q\]and\[\angle R\]
Interior Region: S and T are lies in interior region of \[\Delta PQR.\]
Exterior Region: U and V are lies in exterior region of \[\Delta PQR.\]
Boundary Region: Points lying on the sides of triangle are said to be on boundary region. Point E and F are on boundary region of\[\Delta PQR.\]
Triangular Region: The interior and boundary of triangle together make the triangular region.
CLASSIFICATION OF TRIANGLE
(a) Scalene triangle: A triangle with three unequal side\[AB\ne BC\ne CA\]
(b) Isosceles triangle: A triangle with two equal sides.
\[PQ=PR\]
(c) Equilateral triangle: A triangle with all its three sides equal
\[AB=BC=CA\]
According to Angles
(i) Acute angled triangle: A triangle with all three acute angles is an acute angled triangle\[\angle A,\,\,\angle B\] and\[\angle C\]are all less than\[90{}^\circ \]
(ii) Obtuse angled triangle: A triangle with one obtuse angle and two acute angles is called an obtuse angled triangle. In triangle ABC,\[\angle B\] is obtuse angle, \[\angle A\] and \[\angle C\] are acute angles.
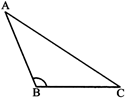
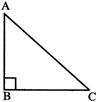
(iii) Right angled triangle: A triangle with one right angle and two acute angles are called a right angled triangle.
\[\angle B\] is right angle. \[\angle A\] and \[\angle C\] are acute angle.
ALTITUDE OF A TRIANGLE
An altitude of a triangle is the perpendicular drawn from a vertex to the opposite side.
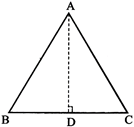
AD is the altitude from A to BC.
Altitude gives the height of the triangle.
MEDIANS OF A TRIANGLE
A median of a triangle is a line segment joining a vertex to the mid-point of the side opposite to that vertex.
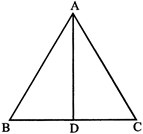
In\[\Delta \]ABC, D is the mid-point of BC, so AD is median.
Note: There are three medians and three altitude in a triangle.
Some Results on Triangle:
PROPERTIES OF TRIANGLE
\[\angle 1+\angle 2+\angle 3=180{}^\circ .\]
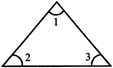
Facts:
EXTERIOR AND INTERIOR OPPOSITE ANGLES
Let the side BC of a \[\Delta ABC\] be produced to \[D.\] Then \[\angle ACD\] is called an exterior angle. \[\angle BAC\] and \[\angle ABC\] are known as interior opposite angles.
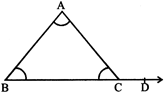
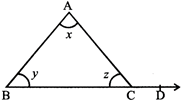
Exterior Angle Property of a Triangle: If any side of a triangle is produced then the exterior angle so formed is equal to the sum of the interior opposite angle.
\[\angle ACD=\angle x+\angle y\]
Triangle Inequality: The sum of any two sides of triangle is greater than the third side. \[x+y>z\] or \[y+z>x\] or \[z+x>y\]
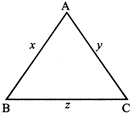
Note: The difference of any two sides of a triangle is less than the third side.
Example: A triangle ABC have different sides as so,
\[AB+BC>CA\]
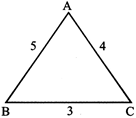
\[5+3>4\]
\[8>4\]
or \[BC+CA>AB\]
\[3+4>5\]
\[7>5\]
or\[AC+AB>BC\]
\[4+5>3\]
\[9>3\]
PYTHAGORAS'S THEOREM
In a right triangle's, the square of hypotenuse equals to the sum of the squares of its remaining two sides.
Thus:
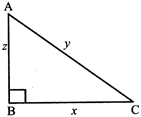
\[\Delta ABC,\,\,\angle B=90{}^\circ \] \[A{{B}^{2}}+B{{C}^{2}}=A{{C}^{2}}\] or \[{{z}^{2}}+{{x}^{2}}={{y}^{2}}\] Example of Pythagoras theorem: The hypotenuse of a right triangle is 17 cm long. If one of the remaining two sides is 8 cm in length, find the length of other side.
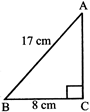
Solution: Let\[\Delta ABC\]be right angled at C
Let AB = 17 cm BC = 8 cm
Then, by Pythagoras' theorem
\[A{{B}^{2}}=B{{C}^{2}}+A{{C}^{2}}\]
\[A{{C}^{2}}=A{{B}^{2}}-B{{C}^{2}}\]
\[={{(17)}^{2}}-{{(8)}^{2}}=289-64=225\]
\[\therefore \] \[AC\Rightarrow \sqrt{225}=15\,cm.\]
Hence the length of the other side is 15 cm.
Two results can be drawn from Pythagoras theorem:
(a) In a right triangle, the hypotenuse is the longest side.
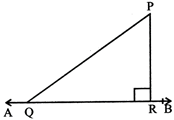
(b) On all the line segments that can be drawn to a given line from a point outside it, the perpendicular line segment is the shortest.
i.e., PR is shortest
CONVERSE OF PYTHAGORAS'S THEOREM
If the square of one side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is right angled. Thus in \[\Delta ABC,\] if\[A{{B}^{2}}=B{{C}^{2}}+C{{A}^{2}},\] then the triangle is right-angled at C.
Pythagorean Triplets: Three positive integers a, b, c in very same order are said to form a Pythagorean triplet, if \[{{c}^{2}}={{a}^{2}}+{{b}^{2}}\]
Thus, each of the triplets (3, 4, 5) (5, 12, 13), (7, 24, 25), (8, 15, 17) is a Pythagorean triplet.
CONGRUENCE OF TRIANGLE
In Geometry, when two figures fit exactly on each other, we call them congruent figures or we say that they are in congruence. The symbol of congruence is s
Example:
(i) Two squares are congruent if their sides are equal
(ii) Two circles are congruent if their radius is equal
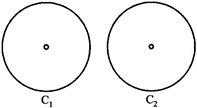
Circle \[{{C}_{1}}\cong \] circle \[{{C}_{2}}\] if radius \[{{C}_{1}}=\] radius \[{{C}_{2}}\]
Congruence of Triangles: Two triangles are congruent if pairs of corresponding sides and corresponding angles are equal.
Thus\[\Delta PQR\cong \Delta ABC\]if.
\[\angle P=\angle A,\] \[PQ=AB\]
\[\angle Q=\angle B\] \[QR=BC\]
\[\angle R=\angle C\] \[RP=CA\]
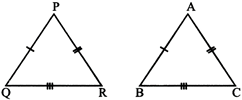
In triangle there are four cases of congruence.
Case 1: (SSS congruence condition) - Two triangles are congruent if the three sides of one triangle are respectively equal to the three sides of the other triangle.
Example:
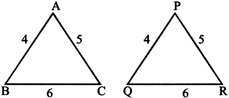
\[\Delta ABC\cong \Delta PQR\]
Case 2: (SAS congruent condition): Two triangles are congruent if the two sides and included angle of one are respectively equal to the two sides and the included angle of the other.
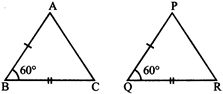
\[AB=PQ\] \[\angle ABC=\angle PQR\]
\[BC=QR\]
So,\[\Delta ABC\cong \Delta PQR\]
Case 3: (ASA congruence condition) - Two triangles are congruent if the two angles and the included side of the one are respectively equal to the two angles and the included side of the other.
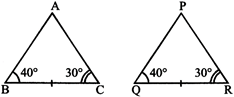
\[BC=QR\]
\[\angle ABC=\angle PQR\]
\[\angle BCA=\angle QRP\]
So,\[\Delta ABC\cong \Delta PQR\]
Case 4: (RHS congruence condition): - Two right triangles are congruent if the hypotenuse and one side of the first triangle are respectively equal to the hypotenuse and one side of second.
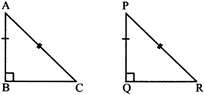
\[AB=PQ\]
\[AC=PR\]
\[\angle ABC\cong \angle PQR\]
Congruence and Area: It is clear that two congruent figures are equal in area. But, there can be two figures which are equal in area but they may not be congruent.
Example: Two rectangles of sides 4 by 5 cm and 10 by 2 cm are equal in area but they are not congruent
Special Properties of Isoceles and Equilateral Triangles:
Property 1. The angles opposite to equal sides of an isosceles triangle are equal.
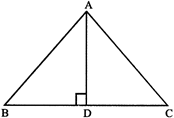
Property 2. In an isosceles and equilateral triangle the perpendicular drawn from the vertex to the base bisects both the vertical angle and the base.
Property 3. If two angles of triangles are equal, then the sides opposite these angles are also equal i.e. the triangle is isosceles.
PRACTICAL GEOMETRY
Construction of a line parallel to a given line through a point not on the line.
Steps:
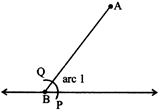
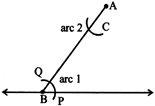
4. Now, with P as center and the same radius as in step 3, draw an arc 2 cutting AB at R.
Elements of Triangle: A triangle has six elements, three sides and three angles. A triangle can be construct if any of these three conditions are fulfilled.
(i) Two sides and the included angle are given.
(ii) One side and two angles are given.
(iii) The three sides of the triangle are given
A triangle can't be construct if:
(a) 3 angles are given or
(b) two sides and a non-included angle are given.
CONSTRUCTION OF TRIANGLES
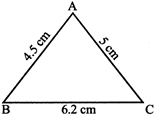
Construct a triangle ABC with AB = 7 cm, BC = 6 cm and AC = 5 cm.
Steps of Construction
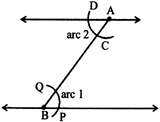
Step 1: Draw a line and mark two points A and B on it such that AB = 7 cm.
![]()
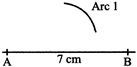
Step 2: Open your compasses to a length of 5 cm draw an arc 1 with A as center.
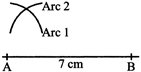
Step 3: Now open your compasses to a length of 6 cm draw an arc 2 with B as center.
Step 4: Label as C the point where the two arcs intersect Join A to C and B to C.
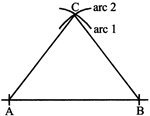
Then the triangle ABC so obtained is the required triangle
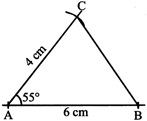
Construct a triangle with AB = 6 cm. AC = 4 cm and\[\angle BAC=55{}^\circ \]
Steps of Construction
Step 1. Draw AB = 6 cm.
![]()
Step 2. Using your protractor draw an angle of \[55{}^\circ \]at A. Make the arm of the angle quite long.
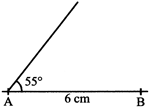
Step 3. Use your compasses to measure the length of AC, i.e. 4 cm, on your ruler and with the point of your compasses A, draw an arc 1 to cut the arm of the angle. This is the point C. Join C and B.
 3.
3.
ASA Construction
Construct a triangle ABC as \[AB=7\,cm,\]\[\angle A=45{}^\circ ,\]\[\angle B=30{}^\circ .\] Calculate the third angle.
Steps of Construction
Step 1. Draw a line segment AB 7 cm long.
![]()
Step 2. Using your protractor, draw an angle BAX of \[45{}^\circ \]at A.
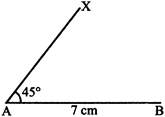
Step 3. Use your protractor to draw the second angle ABY equal to \[30{}^\circ \] at point B. AX and BY meet at C.
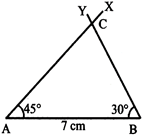
\[\angle A+\angle B+\angle C=180{}^\circ \]
or\[45{}^\circ +30{}^\circ +\angle C=180{}^\circ \]
\[\Rightarrow 75{}^\circ +\angle C=180{}^\circ \]
\[\Rightarrow \angle C=180{}^\circ -75{}^\circ \]
\[\Rightarrow \angle C=105{}^\circ \]
To construct a right triangle when its hypotenuse and one side are given
Construct a right \[\Delta \]ABC, right angled at B, in which AC = 6 cm and AB = 4.5 cm.
Steps of Construction
Step 1. Draw a line segment AB = 4.5 cm and draw BE \[\bot \] AB at B.
Step 2. With A as center and radius = 6 cm draw an arc to cut BE at C.
Step 3. Join A to C.
SYMMETRY
A shape if can fold so that one side fits exactly on the other is known as symmetrical shape. The fold line is known as the line of symmetry, which is also called mirror line.
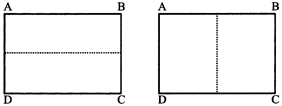
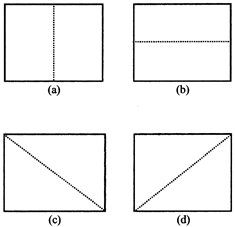
1. Rectangle has two lines of symmetry.
2. Square has four lines of symmetry.
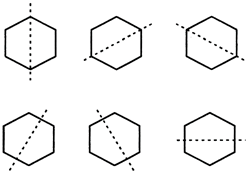
3. A regular hexagon have six lines of symmetry.
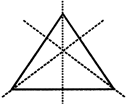
4. An equilateral triangle have three lines of symmetry.
So a regular shape, i.e. shape with equal sides and angles has the same number of lines of symmetry as sides.
5. A line segment is symmetrical about its perpendicular bisector.
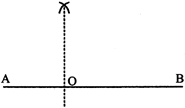
6. An angle with equal arms has one line of symmetry i.e. the bisector of the angle.
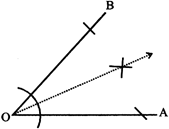
7. An isosceles triangle has one line of symmetry the bisector of the angle included between the equal sides.
8. A semicircle has one line of symmetry.
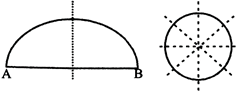
9. A circle has infinite line of symmetry. Symmetry of the letters of the alphabet:

The following letters have no line of symmetry
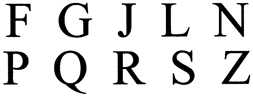
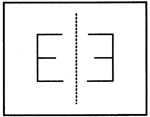
Line of symmetry is also known as mirror line. A reflection in a line produces a mirror image. In a reflection the image is the same size and each point on it is at the same perpendicular distance from the axis of reflection as the corresponding point on the object.
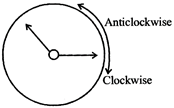
ROTATIONAL SYMMETRY Rotation: Rotation is the movement of an object around a point through a given number of degrees in a clockwise or anticlockwise direction. Example: Figure shows rotation of hands of clock through point O.
Other examples are wheel of bicycle, car, motorcycle, and truck etc., blades of ceiling fan.
Centre of Rotation: When an object rotates, its shape and size do not change. The rotation turns an object about a fixed point. This point is known as center of rotation.
Angle of Rotation: The angle of turning during rotation is called angle of rotation. A fall turn, means \[360{}^\circ ,\] a half turn is \[180{}^\circ \] and a quarter turn is \[90{}^\circ .\]
A figure is said to have rotational symmetry if it fits into itself more than once during a fall turn, i.e. rotation through \[360{}^\circ .\] The number of times the figure fits into itself during rotation by \[360{}^\circ ,\] is called the order of rotational symmetry.
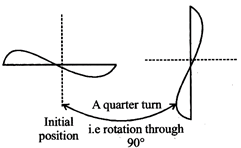
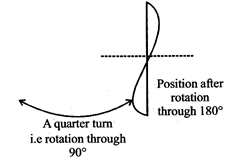
It has a rotational symmetry of order 2
There are some geometrical shapes which have both line symmetry and rotational symmetry such as:
VISUALISING SOLID SHAPES
Any closed three dimensional shape is known as solid.
It has 3-dimensions-length, width and height.
Some solids are:
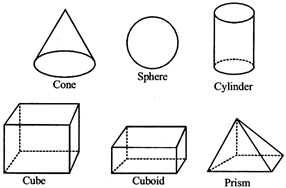
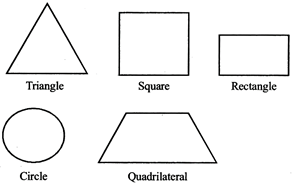
There are some common plane (flat) shapes which can be easily drawn on paper. They have only 2 dimensions -length and breadth.
Some Plane Shapes are:
The different parts of solids are:
| Shape | No. of faces | No. of vertices | No. of edges |
| 1. Cubes | 6 | 8 | 12 |
| 2. Cuboid | 6 | 8 | 12 |
| 3. Cylinder | 3 | Nil | 2 |
| 4. Pyramid (rectangular) | 5 | 5 | 8 |
| 5. Cone | 2 | 1 | 1 |
| 6. Sphere | Nil | Nil | Nil |
Nets of Solid Shapes: A flat shape that can be folded to make a solid shape is called a net.
Net of Cube: It may be following types.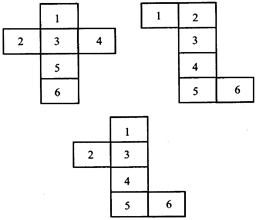
Net of Cuboid:
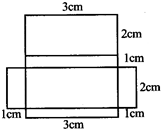
Net of Triangular Box:
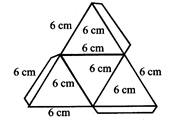
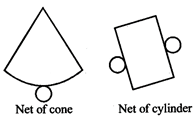
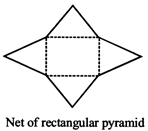
Two Types of Sketches of a Solid are Possible:
(a) An oblique sketch does not have proportional lengths. Still it conveys all important aspects of the appearance of the solid.
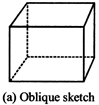
(b) An isometric sketch is drawn on an isometric dot paper. In an isometric sketch of the solid the measurements kept proportional.
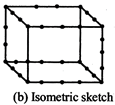
Different Sections of a Solid Can be viewed in Many Ways:
(a) One way is to view by cutting or slicing the shape, which would result in the cross-section of the solid.
(b) Another way is by observing a 2-D shadow of a 3-shape.
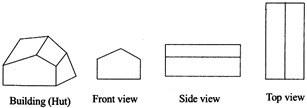
(c) A third ways is to look at the shape from different angles; the front-view, the side-view and the top - view can provide a lot of information about the shape observed.
You need to login to perform this action.
You will be redirected in
3 sec
