Lines and Angles
Category : 7th Class
Lines and Angles
![]()
![]()
![]()
A ray OP is denoted as\[\overrightarrow{OP}\].
The symbol of angle is\[\angle \]. An angle is measured in degrees\[\left( {}^\circ \right)\].
The angle formed by the two rays \[\overrightarrow{AB\,}\,and\,\overrightarrow{AC}\]is denoted by \[\angle \]BAC or \[\angle \]CAB
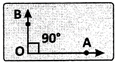
(i) Right angle: An angle whose measure is equal to \[{{90}^{o}}\]is called a right angle.
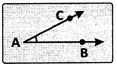
(ii) Acute angle: An angle whose measure is less than 90° is called an acute angle.
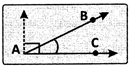
(iii) Obtuse angle: An angle whose measure is greater than 90° but less than 180° is called an obtuse angle.
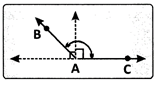
(iv) Straight angle: An angle whose measure is equal to \[{{180}^{o}}\] is called a straight angle.

(v) Complete angle: An angle whose measure is exactly equal to 360° is called a complete angle.
![]()
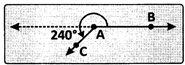

Related Angles:
(i) Complementary angles: Two angles are said to be complementary if the sum of their measures is equal to\[~{{90}^{o}}\].
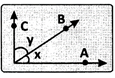
Here \[\angle \]x + \[\angle \]y = 90°, therefore \[\angle \]x and \[\angle \]y are complementary angles.
(iii) Supplementary angles: Two angles are said to be supplementary if the sum of their measures is equal to\[{{180}^{o}}\].
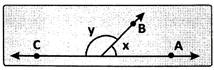
Here, \[\angle \]x + \[\angle \]y = 180°, therefore \[\angle \]x and \[\angle \]y are supplementary angles.
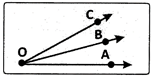
In the figure given, the angles BAC and CAD form a linear pair of angles because the non - common arms AB and AD of the two angles are the opposite rays, with the same vertex A.
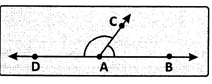
Moreover,\[\angle \]BAC +\[\angle \]DAC = \[{{180}^{o}}\] .
Note: 1. A liner pair is always supplementary.
In the figure given, \[\angle \]BOD and \[\angle \]AOC are a pair of vertically opposite angles because they have common vertex at 0 and also OB, OA; OC, OD are two pairs of opposite rays. Vertically opposite angles are formed when two lines intersect.

Similarly, we find that\[\angle \]BOC and \[\angle \]AOD is another pair of vertically opposite angles. Pair of Lines:
Note: If two lines intersect each other, the vertically opposite angles formed are equal.
Pair of lines:
Transversal: A line which intersects two or more lines at distinct points is called a transversal.
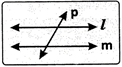
In the given figure, p is a transversal to the lines I and m.
In the figure given, lines I and m are cut by the transversal p. The eight angles marked 1 to 8 have names given in the table.
|
Interior angles |
\[\angle \]3,\[\angle \]4,\[\angle \]5,\[\angle \]6 |
|
Exterior angles |
\[\angle \]1,\[\angle \]2,\[\angle \]7,\[\angle \]8 |
|
Pairs of Corresponding angles |
\[\angle \]1 and \[\angle \]5,\[\angle \]2 and \[\angle \]6,\[\angle \]4 and \[\angle \]8,\[\angle \]3,\[\angle \]6 |
|
Pairs of alternate exterior angles |
\[\angle \]1 and\[\angle \]7,\[\angle \]2 and \[\angle \]8 |
|
Pairs of interior angles on the same side of the transversal |
\[\angle \]4 and \[\angle \]5,\[\angle \]3, and \[\angle \]5 |
(i) If two parallel lines are cut by a transversal, then
(ii) Each pair of corresponding angles is equal.
(iii) Each pair of alternate interior angles is equal.
(iv) Each pair of interior angles on the same side of the transversal is supplementary.
(v) Each pair of alternate exterior angles is equal.
(vi) Each pair of exterior angles on the same side of the transversal is supplementary
Note: (i) The F-Shape stands for fcorrespoding angles.
(ii) The Z- Shape for alternate angels.
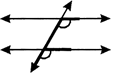
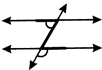
(i) Corresponding angles are equal.
(ii) Alternate interior angles are equal.
(iii) Interior angles on the same side of the transversal are supplementary.
You need to login to perform this action.
You will be redirected in
3 sec
