Parallel Lines
Category : 7th Class
Two lines are said to be parallel if the distance among them always remains same at each and every point. The parallel lines never intersect each other.
In other words we can say that if two lines do not have any common point than they are said to be parallel. In the figure I and m are parallel lines.
![]() Concept of Transversal
Concept of Transversal
Transversal is a line which intersects two or more parallel lines. In the figure, n is a transversal line.
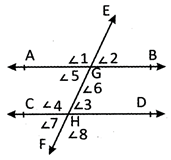
![]() Alternate Interior Angles
Alternate Interior Angles
In the above figure
\[\angle 3\]and \[\angle 5,\text{ }\angle 4\]and \[\angle 6\]are alternate interior angles.
![]() Alternate Exterior Angles
Alternate Exterior Angles
In the above figure \[\angle 7\]and \[\angle 2\]are alternate exterior angles.
![]() Corresponding Angles
Corresponding Angles
\[\angle 2\] and \[\angle 3\] in the above figure are corresponding angles.
They are also the angles on the same side of transversal.
![]() Properties of Angles
Properties of Angles
When the parallel lines are intersected by a transversal:

![]() Using the figure below which one of the following statements is true?
Using the figure below which one of the following statements is true?
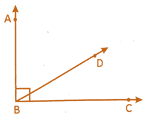
(a) Z ABD and \[\angle ABC\]are adjacent angles
(b) \[\angle ABD\]and \[\angle DBC\]are complementary
(c) \[\angle DBC\]is half of the measure of \[\angle ABC\]
(d) \[\angle ABC\]and Z DBC are congruent
(e) None of these
Answer: (b)
Explanation
From the figure only option (b) is correct because\[\angle ABD+\angle DBC={{90}^{O}}\]
![]() Find the value of x in the figure given below.
Find the value of x in the figure given below.
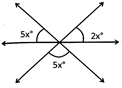
(a)\[15{}^\circ \]
(b) \[20{}^\circ \]
(c)\[9{}^\circ \]
(d) \[15{}^\circ \]
(e) None of these
Answer: (d)
Explanation
From the figure \[5x{}^\circ +5x{}^\circ +2x{}^\circ =180{}^\circ \]
\[\Rightarrow 12x{}^\circ =180{}^\circ \Rightarrow X{}^\circ =15{}^\circ \]
![]() Find the difference between two angles in the figure given below.
Find the difference between two angles in the figure given below.
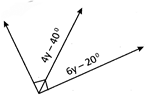
(a)\[15{}^\circ \]
(b) \[50{}^\circ \]
(c)\[70{}^\circ \]
(d) \[20{}^\circ \]
(e) None of these
Answer: (b)
![]() Read the following statements.
Read the following statements.
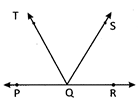
(i) \[\angle PQT\] and \[\angle TQS\] are adjacent angles
(ii) \[\angle TQR\] and \[\angle RQS\] are adjacent angles
(iii) \[\angle TQP\] and \[\angle TQR\] are linear pairs
(iv) \[\angle SQR\] and \[\angle SQT\] are linear pairs
Which one of the following options represents the incorrect statement?
(a) (i), (ii)
(b) (ii), (iii)
(c) (ii), (iv)
(d) (i), (iv)
(e) None of these
Answer: (c)
![]() The angle formed between the bisectors of linear pair is always:
The angle formed between the bisectors of linear pair is always:
(a) An acute angle
(b) An obtuse angle
(c) An angle which is half of the double of the right angle
(d) An acute angle greater than the half of the right angle
(e) None of these
Answer: (c)
![]()
(i) They have a common vertex.
(ii) They have common arm.
(iii) Non common arms is opposite to the common arm.

You need to login to perform this action.
You will be redirected in
3 sec
