7th Class Mathematics Mensuration Circumference and area of a Circle

     Circumference and area of a Circle                  

 

The boundary of the circle is called circumference.                

Circumference of a circle \[=2\pi r.\]  

 

               

 

Find the circumference of a circle whose diameter is 4.2 cm.                

(a) 11.1 cm                                         

(b) 112.2cm                

(c) 13.3cm                                          

(d) 13.2cm                

(e) None of these                

 

Answer: (d)                

Explanation                

Diametre of circle = 4.2 cm                

\[\therefore \]Radius of circle = 2.1 cm                

Circumference \[=2\pi r=2\times \frac{22}{7}\times 2.1=2\times 22\times 0.3=13.2cm\]                

Thus the circumference of this circle = 13.2 cm.  

 

 

               

 

Find the radius of circle whose circumference is 88 m.                

(a) 14m                                                

(b) 15m                

(c) 120m                                              

(d) 25m                

(e) None of these                

 

Answer: (a)                

Explanation                

Circumference (c) = 88 m                

\[C=27\pi r=88\Rightarrow 2\times \frac{22}{7}\times r=88\]                

Or \[r\frac{7\times 88}{2\times 22}=7\times 2=14\,m\]                

Thus the radius of this circle = 14 m  

 

 

 

 

Find the area of a rhombus shaped field, whose each of the sides is 14 cm and the altitude is 1.6 dm.                

(a) \[224c{{m}^{2}}\]                                      

(b)  \[214c{{m}^{3}}\]                

(c) \[224{{m}^{2}}\]                                        

(d) \[224c{{m}^{6}}\]                

(e) None of these                                

 

Answer: (a)                

Explanation                

Base of rhombus = 14 cm                

Altitude = 1.6 dm = 16 cm                

Area of rhombus = Base \[\times \] Altitude                

\[=14\times 16=224c{{m}^{2}}\]                

 

 

  How many tiles \[20cm\times 20cm\] each will be required to pave a footpath 1 m wide carried round the outside of a plot \[28\text{ }m\times 18m\]?                              

(a)  2,400                                             

(b) 5, 2000                        

(c) 9,900                                              

(d) 5, 250                

(e) None of these                                                                                   

 

Answer: (a)                                                        

Explanation                

Area of the outer rectangle                

\[=(2,800+2\times 100)\times (1,800+\text{2}\times 100)=3,000\times 2,000\text{ }c{{m}^{2}}\]                

               

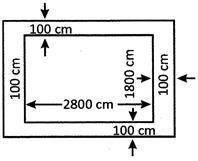
Area of the inner rectangle \[=2,800\times 1,800\,c{{m}^{2}}\]                

Area of the Footpath                

\[=3,000\times 2,000-2,800\times 1,800\text{ }9,60,000\text{ }c{{m}^{2}}\]                

Required number of tiles                

\[=\frac{area\,of\,footpath}{area\,of\,a\,tile}=\frac{9,60,000}{20\times 20}=2,400\]                

 

 

  The base of a parallelogram is twice its height. If the area of parallelogram is \[512\text{ }c{{m}^{2}}\] then find the base.    

(a) \[33c{{m}^{2}}\]                                        

(b) \[32c{{m}^{2}}\]                      

(c) \[40c{{m}^{2}}\]                                         

(d) \[199c{{m}^{2}}\]                

(e) None of these                  

 

Answer: (b)  

 

 

A rhombus of side equal to 65 cm has an area of 2,016 cm2. Find its diagonals.                

(a) 30                                                    

(b) 148                          

(c) 32                                                    

(d) 55                

(e) None of these                                

 

Answer: (c)  

 

 

A parallelogram has sides 60 cm and 40 cm and one of its diagonal is 80cm. Find its area.                

(a) \[600\sqrt{15}cm\]                                   

(b) \[600\text{ }\sqrt{15}\text{ }c{{m}^{2}}\]                

(c) \[650\sqrt{51\,}c{{m}^{2}}\]                                

(d) \[500\text{ }\sqrt{51\,}c{{m}^{2}}\]                

(e) None of these                                

 

Answer: (b)                

 

 

  A wire, when bent in the form of a square, encloses an area of \[484\text{ }c{{m}^{2}}.\] If the same wire is bent in the form of a circle then find the area enclosed by it.                

(a) \[161c{{m}^{2~}}\]                                   

(b) \[616c{{m}^{2}}\]                

(c) \[616\,c{{m}^{2~}}\]                                                

(d) \[916\,c{{m}^{2}}\]                

(e) None of these                

 

Answer: (c)                

Explanation                

Area of square\[~=484\text{ }c{{m}^{2}}\]                

Side of square \[\sqrt{484}=22cm\]                

Perimeter of square \[=4\times 22\text{ }cm=88\text{ }cm\]                

Let r be the radius of the circle.                

Same wire is bent in the form of a square and circle.                

Therefore, circumference of the circle = perimeter of the square.                

or 2\[2\pi r=88\]                

\[2\frac{22}{7}\times r=88\Rightarrow r=\frac{88\times 7}{2\times 22}=14\,cm\]                

Thus area of circle \[=\pi {{r}^{2}}=\frac{22}{7}\times 14\times 14=616\,c{{m}^{2}}\]                

 

 

Semicircular lawns are attached to the edges of a rectangular field measuring \[42\text{ }m\text{ }\times 35m.\] Find the area of the total field. 

(a) \[3895.6{{m}^{2}}~~\]                                             

(b) \[3818.5{{m}^{2}}\]                   

(c) \[3735.6{{m}^{2}}\]                                                  

(d) \[3899.9{{m}^{2}}\]                

(e) None of these                                

 

Answer: (b)                

Explanation                

               

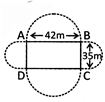
Area of lawn = Area of rectangle \[ABCD\text{ }+2\times \]Area of semicircle with diameter \[AB+2\times \]Area of semicircle with diametre BC                

\[=\text{ }Length\times breadth+2\left( \frac{\pi {{R}^{2}}}{2} \right)+2\left( \frac{\pi {{r}^{2}}}{2} \right)\]                

Where R = radius of bigger semicircle                

\[=\frac{42}{2}=21\,m.\]                

r = radius of smaller semicircle \[=\frac{35}{2}\,m\]                

Now area of lawn                

\[=42\times 35+\frac{22}{7}\times 21\times 21+\frac{22}{7}\times \frac{35}{2}\times \frac{35}{2}\]                

\[=1470+1386++962.5=3818.5\,{{m}^{2}}\]                

 

 

Diametre of a wheel of a bus is 770 cm. How much distance will it cover in 100 revolutions?                

(a) 2.85km                                          

(b) 5.85km                      

(c) 9.85km                                          

(d) 2.42km                

(e) None of these                                

 

Answer: (d)  

 

 

The length of the minute hand of a clock is 10.5 cm long. Find the area swept by the minute hand in 10 minutes.                

(a) \[57.75c{{m}^{2}}\]                                                  

(b) \[95.75c{{m}^{2}}\]                    

(c) \[~85.78c{{m}^{2~}}\]                                             

(d) \[99.99c{{m}^{2}}\]                

(e) None of these                

 

Answer: (a)      

 

 

 

 

• Area of triangle \[=\sqrt{s(s-a)(s-b)(s-c),}s=\frac{a+b+c}{2}\]
• The area of an equilateral triangle \[=\frac{\sqrt{3}}{4}\times {{a}^{2}}\]
• Perimetre of rectangle = 2(Length + breadth)
• Area of rectangle = Length \[\times \] breadth
• Diagonal of rectangle \[\sqrt{{{(length)}^{2}}+{{(breadth)}^{2}}}\]
• Perimetre of parallelogram \[=2\times \]sum of length of adjacent side.
• Area of parallelogram = base \[\times \] corresponding height.
• Perimetre of rhombus \[=4\times \] side
• Area of rhombus = base \[\times \] vertical height or \[\left( \frac{1}{2} \right)\]product of diagonals    

 

 

 

 

• Among the mathematician of ancient Indus Valley and ancient Babylonia there were some surprisingly sophisticated principles that was discovered which is hard to derive some of them without the use of calculus by a modern mathematician.
• Both the Egyptians and the Babylonians were aware of versions of the Pythagorean theorem about 1500 years before Pythagoras; the Egyptians had a correct formula for the volume of a frustum of a square pyramid; the Babylonians had a trigonometry table.