7th Class Mathematics Mensuration Triangles

     Triangles                

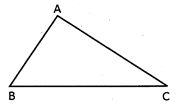
We know that the triangle is a closed region which is bounded by three line segments.

• Perimetre of a triangle = sum of all sides. 

In the following figure perimetre of \[\Delta ABC=AB+BC+CA.\]

• If base  and corresponding height of a triangle is known then the area of a triangle \[=\frac{1}{2}\times base\times height\]

\[=\frac{1}{2}\times b\times h\]                

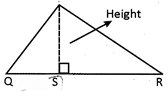
In the given figure area of  \[\Delta PQR\text{ }=\frac{1}{2}\times QR\text{ }\times PS\]                

• If length of all sides of a triangle is known then area of triangle \[=\sqrt{s(s-a)(s-b)(s-c)}\]                

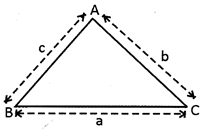
Where s represents half of the perimetre and is equal to \[\frac{a+b+c}{2}\] a, b, c are the length of different sides of a triangle.                

The above formula is also known as Heron's formula.                

• The area of an equilateral triangle \[=\frac{\sqrt{3}}{4}\times {{a}^{2}}\]

Where a is the length of side of an equilateral triangle    

  Find the area of a triangle whose sides are 9 cm, 12 cm and 15 cm.                

(a) 51cm3                                            

(b) 52cm3                       

(c) 53cm4                                            

(d) 54cm2                

(e) None of these                                

Answer: (d)                

Explanation

Here, a = 9 cm, b = 12 cm and c = 15 cm                

\[\therefore S=\frac{a+b+c}{2}=\frac{9+12+15}{2}=\frac{36}{2}=18\]                

Area\[=\sqrt{s(s-a)(s-b)(s-c)}\]\[=\sqrt{s(s-a)(s-b)(s-c)}\]                

\[=\sqrt{18\text{ }\times 9\times 6\text{ }\times 3}=54\text{ }c{{m}^{2}}\]                

A field in the form of a right triangle with hypotenuse 10 m and one side 8 m. Find the are a of the field.                

(a)\[22{{m}^{2}}\]                                          

(b)\[23{{m}^{2}}\]                        

(c)\[24{{m}^{2}}\]                                           

(d) \[25{{m}^{2}}\]                

(e) None of these                                

Answer: (c)                

Given\[AC=10\text{ }m,\text{ }AB=8\text{ }m\]                

By Pythagoras theorem, \[B{{C}^{2}}=A{{C}^{2}}-A{{B}^{2}}=100-64=36\Rightarrow BC=6\text{ }cm\]

Area of \[=\frac{1}{2}\times BC\times AB=\frac{1}{2}\times 6\times 8=24{{m}^{2}}\]                

The base of a triangular field is three times of its altitude. If the cost of .catering the field at Rs. 96 per hectare is Rs. 3600 then find the measure of the base and height.                

(a) (1500m, 500m)          

(b) (900 m, 300 m)                

(c) (500m, 1500m)                           

(d) (400 m, 1200 m)                

(e) None of these                

Answer: (c)  

  The cost of cutting grass from a triangular field at Rs. 45 per 100 m2 is Rs.900. Find its height if twice the base of the triangle is 5 times the height.     

(a) 30m                                                

(b) 40m                         

(c) 50m                                                

(d) 10m                

(e) None of these                

Answer: (b)  

  The area of an equilateral triangle is \[173.2\text{ }c{{m}^{2}}.\] Find the perimeter of the triangle.                

(a) 27.5cm                                          

(b) 4.5cm                       

(c) 60cm                                              

(d) 10cm                

(e) None of these                

Answer: (c)  

       Quadrilaterals                

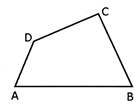
It is the closed geometrical figure which is bounded by four line segments.                

The perimeter of a quadrilateral = sum of all sides                

In the given figure, Perimeter of quadntateral                

\[ABCD\text{ }=AB+BC+CD+DA\]                

The area of quadrilateral is equal to the sum of area of two triangles formed by joining the diagonal. In the given figure area of quadrilateral PQRS = sum of the area of triangle PQR and PRS                

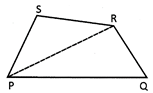
Now we emphasis on areas of some special quadrilateral                

      Rectangle                

It is a quadrilateral whose opposite sides are equal and all angles are right angle.                

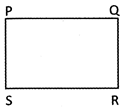
Perimetre of rectangle = 2(Length + breadth)                

Area\[~=\text{ }Length\text{ }\times breadth\]                

\[Length=\frac{breadth}{area},Breadth=\frac{lenadth}{area}\]                

Diagonal \[=\sqrt{{{(length)}^{2}}+{{(breadth)}^{2}}}\]  

      Square                

It is a quadrilateral whose sides are equal and all angles are right angle.                

Perimeter of a square \[=4x\]side                

Area of a square \[=sid{{e}^{2}}=\frac{1}{2}\times {{(diagonal)}^{2}}\]                

\[Diagonal=\text{ }side\sqrt{2}\]  

        Parallelogram                

It is a quadrilateral whose opposite sides are parallel and equal.                

Perimeter \[=2x\]sum of length of adjacent side.                

Area = base x corresponding height.  

        Rhombs                

It is parallelogram whose all sides are equal.                

Perimeter \[=4x\]side                

Area = base \[x\] vertical height or \[\left( \frac{1}{2} \right)\] product of diagonals