Number System
Category : 7th Class
Learning Objectives:
INTEGERS
VARIOUS TYPES OF NUMBERS:
Note: All natural numbers are whole number but zero is the only whole number which is not natural number.
(i) Positive integers: All natural numbers are positive integers such as 1, 2, 3, 4, ............... etc.
(ii) Negative integers: All negative numbers are negative integers such as ...,\[-\,4,-3,-2,-1\]
(iii) Zero is neither negative nor positive integer.
Note:
REPRESENTATION OF INTEGERS ON NUMBER LINE:
Every positive integer is greater than the negative integer.
Zero is less than every positive integer but greater than every negative integer.
ADDITION OF INTEGERS:
Examples: Add:
(i) \[36\,\,\,+27\]
\begin{matrix}
+ & 36 \\
+ & 27 \\
+ & 63 \\
\end{matrix}
(ii) \[-\,36\,\,\,-27\]
\begin{matrix}
- & 36 \\
- & 27 \\
- & 63 \\
\end{matrix}
Examples: Add:
(i) \[+\,36\,\,\,-27\]
\begin{matrix}
+ & 36 \\
- & 27 \\
+ & 9 \\
\end{matrix}
(ii) \[-\,\,36\,\,\,+27\]
\begin{matrix}
- & 36 \\
+ & 27 \\
- & 9 \\
\end{matrix}
PROPERTIES OF ADDITION OF INTEGERS:
Examples:
(i) \[4+3=7,\]which is an integer
(ii) \[4\,+\left( -\,3 \right)=1,\]which is an integer
(iii) \[-\,4+3=-1,\]which is an integer
(iv) \[-\,4+\left( -\,3 \right)=-7,\]which is an integer
Examples:
(i) \[-7+8=1\] and \[8+\left( -\,7 \right)=1\]
\[\therefore \] \[-7+8=8+\left( -\,7 \right)\]
(ii) \[\left( -\,5 \right)+\left( -\,8 \right)=-13\] and \[\left( -\,8 \right)+\left( -\,5 \right)=-13\]
\[\therefore \] \[\left( -\,5 \right)+\left( -\,8 \right)=\left( -\,8 \right)+\left( -\,5 \right)\]
Example: \[\left\{ \left( -\,5 \right)+\left( -\,6 \right) \right\}+7=-11+7=-\,4\]
\[\left( -\,5 \right)+\left\{ \left( -\,6 \right)+7 \right\}=-\,5+1=-\,\,4\]
\[\therefore \] \[\left\{ \left( -\,5 \right)+\left( -\,6 \right) \right\}+7=-\,5+\left\{ \left( -\,6 \right)+7 \right\}\]
Examples:
(i) \[0+9=9+0=9\]
(ii) \[\left( -\,6 \right)+0=0+\left( -\,6 \right)=-\,6\]
(i) The opposite or additive inverse of\[x\]is \[\left( -\,x \right)\] and \[\left( -\,x \right)\] is \[x\]
(ii) The sum of an integer and its opposite is 0.
Example: \[4+\left( -\,4 \right)=0\]and \[\left( -\,4 \right)+4=0\]
So additive inverse of 4 is\[(-\,4)\]and\[(-\,4)\]is 4.
SUBTRACTION OF INTEGERS:
For any integers\[x\]and\[y,\]we define.
(i) \[x-y=x+\](additive inverse of\[y\])\[=x+(-y)\]
(ii) \[x-(-y)=x+\] {additive inverse of \[(-y)\]}\[=x+y\]
PROPERTIES OF SUBTRACTION OF INTEGERS:
Examples:-
(i) \[3-5=-\,2,\]which is an integer
(ii) \[(-\,3)-6=-\,9,\]which is an integer
(iii) \[3-(-\,6)=9,\]which is an integer
(iv) \[(-\,3)-(-\,6)=3,\]which is an integer
Examples:-
(i) Consider the integers 2 and 4, we have
\[(2-4)=2+(-\,4)=-\,2\]and \[(4-4)=2+(-\,4)=-\,2\]
\[\therefore \,\,\,(2-4)\ne (4-2)\]
(ii) Consider the integers\[(-\,5)\]and 3 we have
\[(-\,5)-3=(-\,5)+(-\,3)=-\,8\] and \[3-(-\,5)=8\]
\[\therefore \,\,\,(-\ 5)-3\ne -\,3-3-(-\,5)\]
(iii) Consider the integers\[(-\,6)\]and \[(-\,4),\]we have
\[(-\,6)-(-\,4)=-\,6+4=-\,2\]and\[(-\,4)-(-\,6)=-\,4+6=\,2\]
\[\therefore \,\,(-\,6)-(-\,4)\ne (-\,4)-(-\,6).\]
Consider the integers \[4,\] \[(-\,5)\] and \[(-\,6),\] we have
\[\{4-(-\,5)\}-(-\,6)=(4+5)-(-\,6)=9-(-\,6)\]
\[=9+6=15\]
\[4-\{(-\,5)-(-\,6)\}=4-\{(-\,5)+6\}=4-1=3\]
\[\{4-(-\,5)\}-(-\,6)\ne 4-\{(-\,5)-(-\,6)\}\]
MULTIPLICATION OF INTEGERS:-
Rule 1: To find the product of two integers with unlike sing, first get their product regardless to their signs, the give minus sign to the product.
Examples:
(i) \[(-\,40)\times 9\]
\[=-\,360\]
(ii) \[20\times (-\,3)\]
\[=-\,60\]
Rule 2: To find the product of two integers with like signs, first find their product regardless to their signs then put plus sign to product.
Examples:
(i) \[3\times 5\]
\[=+\,\,15\]
(ii) \[-\,3\times -\,5\]
\[=+\,\,15\]
PROPERTIES OF MULTIPLICATION OF INTEGERS:
Examples:
(i) \[3\times 2=6,\] which is an integer
(ii) \[(-\,3)\times 2=-\,6,\] which is an integer
(iii) \[(-\,3)\times (-\,2)=6,\] which is an integer
(iv) \[\,3\times (-\,2)=-\,6,\]which is an integer
\[(x\times y)=(y\times x)\]
Examples:
(i) \[2\times \left( -\,6 \right)=-12\] and \[\left( -\,6 \right)\times 2=-12\]
\[\therefore \,\,\,2\times \left( -\,6 \right)=\left( -\,6 \right)\times 2\]
(ii) \[\left( -\,3 \right)\times \left( -\,7 \right)=21\] and \[\left( -\,7 \right)\times \left( -\,3 \right)=21\]
\[\therefore \,\,\,\left( -\,3 \right)\times \left( -\,7 \right)=\left( -\,7 \right)\times \left( -\,3 \right)\]
Examples:
(i) Consider the integers \[3,\] \[\left( -\,4 \right)\]and \[\left( -\,5 \right),\] we have
\[\left\{ 3\times \left( -\,4 \right) \right\}\times \left( -\,5 \right)=-\,\,12\times \left( -\,5 \right)=60\] and
\[3\text{ }x\text{ }\left\{ \left( -4 \right)\times \left( -5 \right) \right\}=3\times 20=60\]
\[\therefore \] \[\left\{ 3\times \left( -\,4 \right) \right\}\times \left( -\,5 \right)=3\times \left\{ \left( -\,4 \right)\times \left( -\,5 \right) \right\}\]
(ii) Consider the integers \[\left( -\,5 \right),\left( -\,6 \right)\] and \[\left( -\,7 \right),\] we have
\[\left\{ \left( -\,5 \right)\times \left( -\,6 \right) \right\}\times \left( -\,7 \right)=30\times \left( -\,7 \right)=-\,210\]
\[\left( -\,5 \right)\times \left\{ \left( -\,6 \right)\times \left( -\,7 \right) \right\}=\left( -\,5 \right)\times 42=-\,210\]
\[\therefore \] \[\left\{ \left( -\,5 \right)\times \left( -\,6 \right) \right\}\times \left( -\,7 \right)=\left( -\,5 \right)\times \left\{ \left( -\,6 \right)\times \left( -\,7 \right) \right\}\]
\[x\times \left( y+z \right)=\left( x\times y \right)+\left( x\times z \right)\]
Examples: (1) Consider the integers \[5,\,\left( -\,6 \right)\] and \[\left( -\,7 \right),\]we have
\[5\times \left\{ \left( -\,6 \right)+(-\,7) \right\}=5\times \left( -\,13 \right)=-\,65\] and \[\left\{ 5\times \left( -\,6 \right) \right\}+\left\{ 5\times \left( -\,7 \right) \right\}=-\,30+\left( -\,35 \right)=-\,65\]
\[\therefore \] \[5\times \{(-\,6)+(-\,7)\}=\{5\times (-\,6)\}+\{5\times (-7)\}\]
(2) Consider the integers (-5), (-6) and (-7), we have \[\left( -\,5 \right)\times \left\{ \left( -\,6 \right)+\left( -\,7 \right) \right\}=\left( -\,5 \right)\times \left( -13 \right)=65\] and
\[\left\{ \left( -\,5 \right)\times \left( -\,6 \right) \right\}+\left\{ \left( -\,5 \right)\times \left( -\,7 \right) \right\}=\left( -\,30 \right)+\left( -\,35 \right)=65\]
\[\therefore \,\,\left( -\,5 \right)\times \left\{ \left( -\,6 \right)+\left( -\,7 \right) \right\}=\left\{ \left( -\,5 \right)\times \left( -\,6 \right) \right\}+\left\{ \left( -\,5 \right)\times \left( -\,7 \right) \right\}\]
Examples:
(i) \[13\times 1=13\]
(ii) \[(-12)\times 1=-12\]
\[\frac{1}{x}\]as \[x\left( \frac{1}{x} \right)=\left( \frac{1}{x} \right)\cdot x=1\]
Examples:
(i) Multiplicative inverse of \[5=\frac{1}{5}\]
(ii) Multiplicative inverse of \[-\,5=-\,\frac{1}{5}\]
\[(x\times 0)=(0\times x)=5\]
Examples:
(i) \[5\times 0=0\times 5\text{ }=0\]
(ii) \[(-\,5)\times 0=0\times (-\,5)=0\]
IMPORTANT RESULTS:
DIVISION OF INTEGERS:
Rule 1: To find the division of two integers with unlike sign, first get their quotient regardless to their signs, then give minus sign to the product.
Example:
(i) \[-\,74\div 2\]
\[=\frac{-\,74}{2}\]
\[=-\,37\]
(ii) \[96\div (-\,3)\]
\[=\frac{96}{-\,3}\]
\[=-\,32\]
Rule 2: To find the division of two integers with like signs, first find their product regardless to their signs then put plus sign to quotient.
Example:
(i) \[48\div 6\]
\[=\frac{48}{6}\]
\[=8\]
(ii) \[-\,155\div (-\,5)\]
\[=\frac{-\,155}{-\,5}\]
\[=\,\,31\]
PROPERTIES OF DIVISION OF INTEGERS:
Example:
(i) \[12\] and \[5\] are both integer but \[(12\div 5)\] is not an integer.
(ii) \[(-12)\] and \[5\]are both integer. But \[[(-12)\div 5]\] is not an integer.
Examples:
(i) \[10\div 10=1\] (ii) \[(-\,5)\div (-\,5)=1\]
Examples:
(i) \[5\div 1=5\] (ii) \[(-\,5)\div 1=(-\,5)\]
Examples:
(i) \[0\div 9=0\]
(ii) \[0\div (-\,9)=0\]
(iii) \[6\div 0=\] Meaning less
Thus division on integers is not associative.
Examples: Let \[x=-\,6,y=3,\,z=-\,2\] then,
\[(x\div y)\div z=\{(-\,6)\div 3\}\div (-\,2)=(-\,2)\div (-\,2)=1\]
\[x\div \{(y)\div (z)\}=(-\,6)\div \{3\div (-\,2)\}=(-\,6)\div (-1.5)=4\]
\[\therefore \] \[(x\div y)\div z\ne x\div \{(y)\div (z)\}\]
If \[x=-\,6,y=3\]and\[z=1\]then.
\[(x\div y)\div z=\{(-\,6)\div 3\}\div 1=(-\,2)\div 1=-\,2\]
\[x\div \{(y)\div z\}=(-\,6)\div \{3+1\}=(-\,6)\div 3=-\,2\]
So, \[(x\div y)\div z=x\div \{y\div z\}\]
(i) \[(x\div z)>(y\div z)\] if \[z\] is positive
(ii) \[(x\div z)<(y\div z)\] if \[z\] is negative
Example:-
(i) If\[x=27,y=18\]and\[z=9\]
\[(x\div z)>(y\div z)\]
\[(27\div 9)>(18\div 9)\]
\[3>2\]
(ii) If \[x=27,y=18\]and \[z=-\,9\]
\[(x\div z)<(y\div z)\]
\[\{27\div (-\,9)\}<\{18\div (-\,9)\}\]
\[-\,3<-\,2\]
Use of Brackets:
We know that the priority order of different mathematical operations is
(1) Division (2) Multiplication
(3) Addition (4) Subtraction
Sometimes in complex expressions, we require a set of operations to be performed prior to the others.
Here we make use of brackets. Brackets which are commonly used are: -
|
Brackets |
Name |
|
( ) |
Parentheses or common brackets |
|
{ } |
Braces or curly brackets |
|
[ ] |
Square or Box brackets |
|
— |
Vinculum |
For examples, \[\frac{3}{5}+\frac{7}{2}\]
LCM of \[5,\,2=10\]
Like fraction \[\Rightarrow \frac{3}{5}=\frac{6}{10}\]and\[\frac{7}{2}=\frac{35}{10}\]
\[\frac{6}{10}+\frac{35}{10}=\frac{41}{10}\]
MULTIPLICATION AND SUBTRACTION OF FRACTIONS
To multiply a mixed fraction by a whole number, first convert it into an improper fraction and then multiply.
FRACTIONAS AN OPERATOR ‘OF’

Observe this figure. The two squares are exactly same.
Each shaded portion represents \[\frac{1}{2}\]of 1.
So, both the shaded portions together will represent \[\frac{1}{2}\] of 2.
Combine the 2 shaded\[\frac{1}{2}\]parts. It represents 1.
So, we say \[\frac{1}{2}\] of 2 is 1. We can also get it as\[\frac{1}{2}\times 2=1.\]
Thus, \[\frac{1}{2}\] of \[2=\frac{1}{2}\times 2=1\]
\[\text{In}\,\text{general}\,\text{product}\,\text{of}\,\text{fractions}\]
\[\,\text{=}\,\,\frac{\text{Product}\,\text{of}\,\text{Numerators}}{\text{Product}\,\text{of}\,\text{Denominators}}\]
The value of the product of two improper fractions is more than each of the two fractions.
DIVISION OF FRACTIONS
For example, \[6\div \frac{2}{3}\Rightarrow 6\times \frac{3}{2}=9\]
The non-zero numbers whose product with each other is 1 are called reciprocals of each other.
H.C.F. AND L.C.M.
The H.C.F. of given numbers is not greater than any of the given numbers.
The L.C.M. of given numbers is not less than any of the given numbers.
H.C.F. of two numbers always divides their L.C.M.
The H.C.F. of two co-prime numbers is 1.
The L.C.M. of two co-prime numbers is product of the numbers.
The product of the H.C.F. and the L.C.M. of the two given numbers is equal to the product of those numbers, i.e.,
H.C.F.\[\times \]L.C.M. = Product of the given numbers.
Example: The HCF of two numbers is 9 and their LCM is 270. If the sum of the numbers is 99, their difference is equal to
Solution:
Let the numbers be \[x\] and \[99-x.\]
So \[x\times (99-x)=9\times 270\]
On solving the above equation, we get; \[x=54,\] or\[45\]
So difference will be\[54-45=9.\]
FACTOR THEOREM
If \[\left( x+a \right)\] is a factor of polynomial\[P(x),\]then remainder\[=0\]
\[\Rightarrow P(-\,a)=0\]
Example: Show that \[(x-3)\] is a factor of the polynomial
\[P(x)={{x}^{3}}-3{{x}^{2}}+4x-12\]
lf \[(x-3)\] is a factor of polynomial
\[P(x)={{x}^{3}}-3{{x}^{2}}+4x-12,\] then remainder
\[P(3)=0\]
\[P(3)=0\]
\[P(3)={{3}^{3}}-3\times {{3}^{2}}+4\times 3-12\]
\[=27-27+12-12=0\]
As remainder\[P(3)=0\]
\[\therefore \] \[(x-3)\] is a factor of polynomial\[P\,(x)\].
PROPERTIES OF DECIMALS
Thus, in 63.825
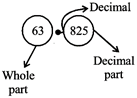
Example: 6.438 have three digits in decimal part which is known as three decimal places.
Example: 6.238, 38.937, 48.385 are like decimals.
Example: 6.238, 32.73, 65.3984 are unlike decimals.
Remember: On adding zeros after the last digit of the decimal part of any decimal number does not change the value of the decimal.
Example: 6.28 can be 6.280 or 6.2800 but the value of all three are same.
We use this property to convert the unlike decimal into like decimal.
COMPARINGDEOMALS:
Suppose we have to compare two given decimals. We follow the following steps:
Example: Compare the following digits.
5.74, 6.03, 0.8, 0.648 and 8.2.
Solution: Converting the given numbers into like decimals we get them as:
5.740, 6.030, 0.800, 0.648 and 8.200
Clearly 0.648 < 0.800 < 5.740 < 6.030 < 8.200
CONVERSION OFDEOMAL INTO FRACTION:
Example: Convert 2.85 into fraction.
Solution: \[\frac{285}{100}=\frac{57}{20}\]
CONVERSION OFA FRACTION INTO DECIMAL:
Example: Convert \[\frac{27}{4}\] and \[2\frac{3}{8}\] into decimal fraction.
Solution: \[\frac{27}{4}\]
\[4\,\underset{\times \,\times }{\mathop{\underline{\underset{\,\,\,\,-\,20}{\mathop{\underset{\,\,\,\,\,\,\,\,\,\,\,20}{\mathop{\overset{6.75}{\mathop{\underline{\underset{-28}{\mathop{\underset{30}{\mathop{\overline{\underline{\underset{-\,24}{\mathop{)\,\,\,27.00}}\,\,\,\,\,}}}}\,}}\,}}}\,}}\,}}\,}}}\,\]
\[\therefore \] \[\frac{27}{4}=6.75\]
and \[2\frac{3}{8}=\frac{19}{8}\]
\[8\,\underset{\times \,\times }{\mathop{\underline{\underset{-\,40}{\mathop{\underset{40}{\mathop{\underline{\underset{\,\,\,\,-\,56}{\mathop{\underset{\,\,\,\,\,\,\,\,\,\,\,60}{\mathop{\overset{2.375}{\mathop{\underline{\underset{-24}{\mathop{\underset{30}{\mathop{\overline{\underline{\underset{-\,16}{\mathop{)\,\,19.000}}\,\,\,\,\,}}}}\,}}\,}}}\,}}\,}}\,}}}\,}}\,}}}\,\]
\[\therefore \] \[2\frac{3}{8}=2.375\]
ADDITIONAND SUBTRACTION OF DECIMAL NUMBERS:
Method:
(i) Write the given numbers one below the other with decimal points in vertical line.
(ii) Equal the digits of numbers by adding zeros at right extremes of decimal parts as required.
(iii) Then add or subtract the numbers and put decimal in result directly under the other decimal points.
Example:
(i) Add: 0.872, 3.46, 4.309, and 3.17
Solution:
\[\underline{\begin{align}
& \underline{\begin{align}
& \,\,\,\,0.872 \\
& \,\,\,\,3.460 \\
& \,\,\,\,4.309 \\
& +\,3.170 \\
\end{align}} \\
& \,\,11.811 \\
\end{align}}\]
(ii) Subtract: 17.182 from 360.05
\[\underline{\begin{align}
& \underline{\begin{align}
& \,\,\,\,360.050 \\
& -\,017.182 \\
\end{align}} \\
& 342.868 \\
\end{align}}\]
MULTIPLICATION OF DECIMAL NUMBERS:
(1) To multiply a decimal number by 10 or any power of 10 move the decimal point as many places to the right as there are zeros in the multiplier or we can say that multiplying a decimal number by \[{{10}^{n}}\] moves the decimal point\[n\]places to the right.
Examples:
![]()
![]()
![]()
(2) To multiply a decimal number by a whole number or a decimal number multiply the numbers first as there were no decimal point at all and fix the position by the rule that there are as many decimal places in the product as they are in multiplier and multiplicand put together.
Example:
(1) \[\underset{\text{1}\,\,\text{place}}{\mathop{0.6}}\,\times \underset{\text{2}\,\,\text{places}}{\mathop{0.02}}\,=\underset{\text{3}\,\,\text{places}}{\mathop{0.012}}\,\]
(2) \[\underset{0\,\,\text{place}}{\mathop{7\,}}\,\,\,\,\times \underset{3\,\,\text{places}}{\mathop{\,0.003}}\,\,\,\,\,=\underset{\text{3}\,\,\text{places}}{\mathop{\,0.021\,}}\,\]
DIVISION OF DECIMAL NUMBERS
(1) Dividing a whole number or decimal number by \[10\] or any higher power of \[10\,({{10}^{n}})\] move the decimal point that number of places \[(n)\] to the left.
Examples: (1) \[53\div 10=5.3\]
(2) \[53\div 100=0.53\]
(3) \[53\div 1000=0.053\]
(2) To divide a decimal number by a whole number proceed as with whole numbers, but place the decimal point in the quotient directly above or below the decimal point in the dividend.
Example: (1) Divide 15.064 by 28

\[\therefore \] \[15.064\div 28=0.538\]
(2) Divide 24.2 by 55000
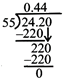
\[\because \,\,\,24.50\div 55=0.44\] \[\]
\[\because \,\,\,24.20\div 55000=0.0004\]
(3) To divide a decimal number by a decimal number move the decimal point of divisor to the right until it becomes a whole number (i.e., multiply it by 10 or a power of 10). Then move the decimal point of the dividend the same number of places to the right, adding zero if necessary.
Example: Divide 49.08 by 0.012
Solution: \[49.08\times 1000=49080\]
\[0.012\times 1000=12\] \[\]
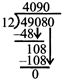
RATIONAL NUMBER
A number in form of \[\frac{a}{b}\] where \[a\] and \[b\] are integers and \[b\ne 0\] is known as rational number.
Examples: \[\frac{1}{2},\frac{-\,6}{7},\frac{3}{-\,2},\frac{-\,5}{-\,8}\]is a rational number.
Remember:
Example: \[1=\frac{1}{1},2=\frac{2}{1},3=\frac{3}{1}\,\,.......\,\,\frac{n}{1}\]are integers but rational number like \[\frac{5}{7},\frac{-\,8}{9},\frac{11}{-13}\] are not integers.
Let \[\frac{a}{b}\] is a fraction where \[a\] and \[b\] are natural numbers. Since every natural number is \[a\] integer so \[a\] and \[b\] are integers so fraction \[\frac{a}{b}\] where \[b\ne 0\] is a rational number.
Example:
A number like \[\frac{5}{-\,6}\] is a rational number is not a fraction because its denominator \[-\,6\] is not a natural number.
Positive rational number: A rational number is said to be positive rational number if both the numerator and denominator are positive or negative.
Examples: \[\frac{5}{7},\frac{-18}{-\,27},\frac{-16}{-13},\frac{8}{9}\]
Negative rational numbers: A rational number is said to be negative if its numerator and denominator are such that one of them is positive and another is negative.
Example: \[\frac{-\,3}{4},\frac{8}{-\,6},\frac{-\,28}{11}\]
Remember:
Example: \[-1,-\,2,-\,3.......\] may be written as: \[-\frac{1}{1},\frac{-\,2}{1},\frac{-\,3}{1}........\] are all negative rational numbers.
TWO IMPORTANT PROPERTDES OF RATIONAL NUMBERS:
Property 1: Equivalent rational numbers \[\div \] If \[\frac{a}{b}\] is a rational number and \[n\] is a non-zero integer then on multiplying the numerator and denominator of rational number by \[n\] we will get its equivalent rational number as \[\frac{a}{b}=\frac{a\times n}{b\times n}\]
Examples: \[-\frac{3}{4}=\frac{(-\,3)\times 2}{4\times 2}=\frac{(-\,3)\times 3}{4\times 3}=\frac{(-\,3)\times 4}{4\times 4}=.....\]
All these rational numbers are equal to one another and are called equivalent rational numbers.
Property 2: Reducing to simpler form
If \[\frac{a}{b}\] is a rational number and \[n\] is a common divisor of \[a\] and \[b\] then \[\frac{a}{b}=\frac{a\div n}{b\div n}\]
Examples: \[-\frac{48}{60}=\frac{-48\div 2}{60\div 2}=\frac{-48\div 3}{60\div 3}=\frac{-48\div 4}{60\div 4}\]
\[=\frac{-48\div 6}{60\div 6}=\frac{-48\div 12}{60\div 12}\]
\[\Rightarrow -\frac{48}{60}=\frac{-24}{30}=\frac{-16}{20}=\frac{-12}{15}=\frac{-8}{10}=\frac{-4}{5}\]
The rational number \[\frac{-\,4}{5}\] is in lowest number.
STANDARD FORM:
A rational number is said to be in its standard form when its denominator is positive and it is in its lowest term.
Rational number can be in its standard form by following steps-
Example: Convert the following in their standard form.
(i) \[2\frac{4}{9}\]
\[=\frac{22}{9}\]
(ii) \[-\frac{8}{2}\]
\[-\frac{8\div 2}{2\div 2}=-\,4\]
(iii) \[\frac{4}{-11}\]
\[=\frac{4}{-11}\times \frac{-1}{-1}=\frac{-\,4}{11}\]
(iv) \[\frac{9}{15}\]
HCF of 9 and 15 is 3
so \[\frac{9\div 3}{15\div 3}=\frac{3}{5}\]
Note: If the denominator of rational number is negative then multiply both the numerator and denominator by \[-1\] to make denominator positive.
RATIONAL NUMBER ON NUMBER LINE:
To express rational numbers on appropriate number lines, divide the unit length into the number of equal parts as the denominator of the rational number and then mark the numbers on the line.
Example: \[P=\frac{7}{8},\,\,Q=\frac{-\,3}{8},\,\,R=\frac{1}{8},\,\,S=\frac{1}{-\,8}\]

EQUALITY OF RATIONAL NUMBERS:
Two rational numbers \[\frac{a}{b}\] and \[\frac{c}{d}\] are equal \[\frac{a}{b}=\frac{c}{d}\] if \[a\times d=b\times c.\]
Example: \[\frac{-24}{27}=\frac{8}{-9}\]
![]()
\[-\,24\times -\,9=27\times 8\]
\[216=216\]
COMPARISON OF TWO RATIONAL NUMBERS:
Positive rational numbers are always greater than negative rational numbers. But if we have to compare two positive or two negative rational numbers we compare them by two methods.
First Method:
(a) Express each rational number with its positive denominator.
(b) Find LCM of positive denominators.
(c) Express each given rational numbers with LCM as the common denominator.
(d) The number having greater numerator is greater.
Example: Compare:
(i) \[\frac{9}{15}\] and \[\frac{11}{6}\]
LCM of 15 and \[6=3\times 5\times 2=30\]
\[\frac{9\times 2}{15\times 2}=\frac{18}{30},\frac{11\times 5}{6\times 5}=\frac{55}{30}\]
\[\frac{55}{30}>\frac{18}{30},\]So, \[\frac{11}{6}>\frac{9}{15}\]
(ii) \[\frac{3}{-14}\]and\[-\frac{5}{21}\]
\[\frac{3}{-14}\]and\[-\frac{5}{21}\]
LCM of 14 and \[21=2\times 7\times 3=42\]
\[-\frac{3\times 3}{14\times 3}=\frac{-9}{42},\frac{-5\times 2}{21\times 2}=\frac{-10}{42}\]
\[\frac{-9}{42}>\frac{-10}{42}\]
So, \[\frac{-3}{14}>\frac{-5}{12}\]
Second Method:
To compare two rational numbers \[\frac{a}{b}\] and \[\frac{c}{d},\] we compare the products \[a\times d\] and \[b\times c\] define their inequality accordingly.
![]()
If \[a\times d>b\times c\] If \[a\times d<b\times c\]
then \[\frac{a}{b}>\frac{c}{d}\] then \[\frac{a}{b}<\frac{c}{d}\]
Example: Compare \[\frac{-5}{9}\] and \[\frac{11}{-16}\]
First \[-\frac{5}{9}\] and \[-\frac{11}{16}\]
Now, \[-\,5\times 16\] and \[9\times -\,11\]
So, \[-\,80>-\,99\]
So, \[-\,\frac{5}{9}>-\,\frac{11}{16}\]
ORDER PROPERTIES OF RATIONAL NUMBERS:
Property 1: For each rational number \[a,\] exactly one of the following is true.
(i) \[a>0\] (ii) \[a=0\]
(iii) \[a<0\]
Property 2: For any two rational numbers \[a\] and \[b\] exactly, one of the following is true.
(i) \[a>b\] (ii) \[a=0\]
(iii) \[a<b\]
Property 3: lf a, b and c are any three rational numbers such that a > b and b > c, then a > c
ABSOLUTE VALUE OF RATIONAL NUMBERS:
The absolute value of an integer is an integer similarly the absolute value of a rational number is a rational number regardless to their signs.
Thus\[\left| \frac{5}{7} \right|=\frac{5}{7};\left| \frac{-5}{7} \right|=\frac{\left| -5 \right|}{\left| 7\, \right|}=\frac{5}{7};\left| \frac{65}{-23} \right|=\frac{\left| 65 \right|}{\left| -23 \right|}=\frac{65}{23}\]
OPERATIONS ON RATIONAL NUMBERS:
Case 1. When denominators of given rational numbers are equal
Let \[\frac{p}{q}\] and \[\frac{r}{q}\] are two rational numbers. Then \[\frac{p}{q}+\frac{r}{q}\]or \[\left( \frac{p+r}{q} \right)\]
Example: Add- \[\frac{7}{-11}\] and \[\frac{3}{11}\]
\[\frac{-7}{11}+\frac{3}{11}=\frac{-7+3}{11}=\frac{-4}{11}\]
Case 2: When denominator of given numbers are unequal.
Example: Add: \[\frac{7}{-\,27}+\frac{11}{18}-\frac{7}{27}+\frac{11}{18}\]
LCM of 27 and \[18=3\times 3\times 3\times 2=54\]
\[-\frac{7\times 20}{27\times 2}=-\frac{14}{54}\]and\[\frac{11\times 3}{18\times 3}=\frac{33}{54}\]
\[\therefore \,\,\,\frac{-14}{54}+\frac{33}{34}=\frac{-14+33}{54}=\frac{19}{54}\]
2 Subtraction of Rational Number: If \[\frac{a}{b}\] and \[\frac{c}{d}\] are two rational numbers, then
\[\frac{a}{b}-\frac{c}{d}=\frac{a}{b}+\left\{ \text{Additive}\,\text{inverse}\,\text{or}\,\text{negative}\,\text{of}\frac{c}{d} \right\}\] \[\frac{a}{b}-\frac{c}{d}=\frac{a}{b}+\left( -\frac{c}{d} \right)\]
Example: Subtract (i) \[\frac{7}{8}\] from \[\frac{5}{12}\]
\[\frac{5}{12}-\frac{7}{8}=\frac{5}{12}+\frac{-\,7}{8}\]
LCM of 12 and \[8=2\times 2\times 3\times 2=24\]
\[=\frac{5\times 2+(-7)\times 3}{24}=\frac{10+(-21)}{24}=\frac{-11}{24}\]
(ii) \[\frac{-4}{9}\]from \[\frac{-7}{18}\]
\[\frac{-7}{18}-\left( \frac{-\,4}{9} \right)\]
\[\frac{-7}{18}+\left[ -\left( \frac{-\,4}{9} \right) \right]\]
\[-\frac{7}{18}+\frac{4}{9}\]
LCM of 18 and \[9=9\times 2=18\]
\[\frac{(-7)\times 1+4\times 2}{18}=\frac{-7+8}{18}=\frac{1}{18}\]
\[\text{Product of two rational numbers}\]
\[=\frac{\text{Product}\,\text{of}\,\text{numerators}}{\text{Product}\,\text{of}\,\text{denominator}}\]
Thus if \[\frac{a}{b}\] and \[\frac{c}{d}\] are two rational numbers, then \[\frac{a}{b}\times \frac{c}{d}=\frac{a\times c}{b\times d}\]
Example: (i) \[\frac{-7}{15}\times \frac{5}{-14}=\frac{-7\times 5}{15\times -14}=\frac{-35}{-210}=\frac{1}{6}\]
(ii) \[\frac{-7}{9}\times \frac{-4}{5}=\frac{28}{45}\]
RECIPROCALOR MULTIPLICATIVE INVERSE OF A RATIONAL NUMBER:
The reciprocal of a rational number \[\frac{a}{b}\] is \[\frac{b}{a}\] or \[{{\left( \frac{a}{b} \right)}^{-1}}=\frac{b}{a}\]
Note: (i) Reciprocal of 0 does not exist.
(ii) Reciprocal of 1 is 1
(iii) Reciprocal of\[-1\] is\[-1\].
Example: Write reciprocal of:
(i) \[\frac{12}{7}\] (ii) \[\frac{-7}{9}\]
(iii) \[-5\]
Solution:
(i) \[\frac{12}{7}\]
(ii) \[\frac{-7}{9}\]
reciprocal\[=\frac{7}{12}\] \[\frac{9}{-7}\]
(iii) \[-5\,{{(-5)}^{-1}}=\frac{1}{-5}\]
DIVISION OF RATIONAL NUMBERS:
If \[\frac{a}{b}\] and \[\frac{c}{d}\] are two rational numbers such that \[\frac{c}{d}\] then,
\[\frac{a}{b}-\frac{c}{d}=\frac{a}{b}\times \left( \text{reciorocal}\,\text{of}\,\frac{c}{d} \right)=\frac{a}{b}\times \frac{d}{c}\]
Example:
(i) \[\frac{7}{15}\div \frac{2}{3}=\frac{7}{15}\times \left( \text{reciorocal}\,\text{of}\,\frac{2}{3} \right)=\frac{7}{15}\times \frac{3}{2}=\frac{7}{10}\]
(ii) \[\frac{16}{21}\div \frac{-4}{3}=\frac{16}{21}\times \left( \text{reciorocal}\,\text{of}\,\frac{-4}{3} \right)=\frac{16}{21}\times \frac{3}{-4}=\frac{-4}{7}\]
You need to login to perform this action.
You will be redirected in
3 sec
