7th Class Mathematics Rational Numbers

Rational Numbers

• Natural numbers (N): 1, 2, 3, 4 ... etc., are called natural numbers.
• Whole numbers (W): 0, 1, 2, 3...... etc., are called whole numbers.
• Integers (Z): ....... -3, -2, -1, 0, 1, 2, 3 …… etc., are called integers, denoted by I or Z.

            1, 2, 3, 4, etc., are called positive integers denoted by 7. \[{{Z}^{+}}\].

            -1, -2, - 3, - 4,...... etc., are called negative integers denoted by Z-

            Note:  0 is neither positive nor negative.

• Fractions:

            The numbers of the form \[\frac{x}{y}\], where x and y are natural numbers, are known as fractions.

            e.g.\[\frac{3}{5},\frac{2}{1},\frac{1}{125},\]......... etc.

• Rational numbers (Q):

            A number of the form \[\frac{p}{q}\](q\[\ne \]O), where p and q are integers is called a rational number.

            e.g.,\[\frac{-3}{17},\frac{5}{-19},\frac{10}{1},\frac{-11}{-23},\]…. etc.

            Note: 0 is a rational number, since 0=\[\frac{\mathbf{0}}{\mathbf{1}}\].

• A rational number r- is positive if p and q are either both positive and both negative.

            e.g., \[\frac{3}{5},\frac{-2}{-7}\]

• A rational number \[\frac{p}{q}\]is negative if either of p and q is positive and the other is negative.

            e.g., \[\frac{-5}{3},\frac{7}{-23}\]

            Note: 0 is neither a positive nor a negative rational number.

• Representation of Rational numbers on a number line:

            We can mark rational numbers on a number line just as we do integers.

            The negative rational numbers are marked to the left of 0 and the positive rational numbers are marked to the right of 0.

            Thus,,\[\frac{1}{3}and-\frac{1}{3}\]would be at an equal distance from 0 but on its either side.

            Similarly, other rational numbers with different denominators can also be represented on the number line.

            Thus, in general, any rational number is either of the following two types.

            (i)\[\frac{m}{n}\] where m < n   (ii)\[\frac{m}{n}\] where m > n

            e.g., 4, 6 \[\frac{1}{2},\frac{3}{4},\frac{5}{6}\]etc.,

            e.g.,\[\frac{7}{6},\frac{3}{2},\frac{15}{6}\] etc.     

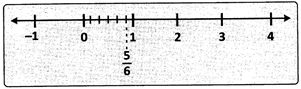
            Representation of\[\frac{\mathbf{m}}{\mathbf{n}}\] on the number line where m < n:

            The rational number - (5 < 6) is represented on the number line as shown.

• Representation of \[\frac{\mathbf{m}}{\mathbf{n}}\]on the number line where m > n:

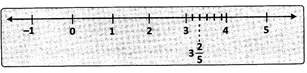
            Consider the rational number \[\frac{17}{5}\].

            First convert the rational number\[\frac{17}{5}\]into a mixed fraction and then mark it on the number line i.e.  

• Standard form of a rational number:

            A rational number'\[\frac{p}{q}\]is said to be in standard form if q is a positive integer and the integers p and q have no common factor other than 1.

• Comparison of two rational numbers:

            Step 1: Express each of the two given rational numbers with a positive denominator.

            Step 2: Take the L.C.M. of these positive denominators.

            Step 3: Express each rational number with this L.C.M. as common denominator.

            Step 4: The number having a greater numerator is greater.

• Rational numbers between two rational numbers:

• There exist infinitely many rational numbers between any two rational numbers. So, we can insert any number of rational numbers between any two given rational numbers.

• Operations on rational numbers:

            (i) Addition: To add two rational numbers with the same denominator, we simply add their numerators and divide by the common denominator.

            e.g., \[\frac{-15}{7}+\frac{1}{7}=\frac{-5+1}{7}=\frac{-4}{7}\]

            When denominators of given rational numbers are different find their L.C.M and express each one of the given rational numbers with this L.C.M as the common denominator. Then add as usual.

            Additive Inverse:

            \[\frac{-p}{q}\]is the additive inverse of\[\frac{p}{q}and\frac{p}{q}\] and\[\frac{-p}{q}\]is the additive inverse of

            e.g.,\[\frac{-2}{5}+\frac{2}{5}=0=\frac{2}{5}+\left( \frac{-2}{5} \right).\]

• The sum of a number and its additive inverse is 0 (the additive identity).

            Subtraction: While subtracting two rational numbers, we add the additive inverse of the rational number to be subtracted to the other rational number.

            Thus, \[\frac{-2}{5}+\frac{2}{5}=0=\frac{2}{5}+\left( \frac{-2}{5} \right).\]additive inverse of

            \[\frac{2}{3}=\frac{7}{8}+\frac{\left( -2 \right)}{3}=\frac{21+\left( -16 \right)}{24}=\frac{5}{24}\]

• Multiplication: To multiply two rational numbers, we multiply their numerators and

            Product of the numerators denominators separately and write the product as 

            \[\frac{Product\,of\,the\,numbers}{Product of the denominators}\]

• Thus, for any two rational numbers \[\frac{a}{b}and\frac{c}{d}\], their product is \[\left( \frac{a}{b}\times \frac{c}{d} \right)=\left( \frac{a\times c}{b\times d} \right).\]

            Reciprocal of a rational number: If the product of two rational numbers is 1 then each rational number is called the reciprocal of the other.

• Thus, the reciprocal of\[\frac{a}{b}is\frac{c}{d}\] and we write,\[{{\left( \frac{a}{b} \right)}^{-1}}=\frac{b}{a}\]

            Clearly, (a) reciprocal of 0 does not exist.

            (b) reciprocal of 1 does not exist.

            (c) reciprocal of-1 is-1.

• Division: To divide one rational number by another non-zero rational number, we multiply the rational number by the reciprocal of the other.

            Thus, if\[\frac{a}{b}\,and\,\frac{c}{d}\]are two rational numbers such that\[\frac{c}{d}\ne 0\].

            then\[\left( \frac{a}{b}\div \frac{c}{d} \right)=\frac{a}{b}\times \left( reciprocal\,\frac{c}{d} \right)=\left( \frac{a}{b}\times \frac{d}{c} \right)\]

            e.g.,\[\frac{-7}{2}\div \frac{4}{3}=\frac{-7}{2}\times \left( Reciprocal\,of\,\frac{4}{3} \right)=\frac{-7}{2}\times \frac{3}{4}=\frac{-21}{8}\]