Basic Concepts of Triangles
Category : 7th Class
The general shape of a triangle is shown below:
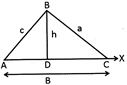
The vertices of a triangle are denoted by the Capital letters of English alphabets.
In the above figure \[\Delta ABC,\]the sides are AB, BC and CA.
![]() Altitude
Altitude
A Perpendicular drawn from a vertex to the opposite side is called the altitude of the triangle and denoted as h.
![]() Some Basic Facts Related to Triangle
Some Basic Facts Related to Triangle
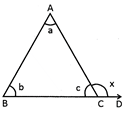
Proof: In \[\Delta ABC,a+b+c=180{}^\circ \]
but,\[c+x=180{}^\circ \] (Linear pair) \[c={{180}^{0}}-x\]
Putting "c" in the above equation, we get
\[a+b+180{}^\circ -x=180{}^\circ \Rightarrow a+b=x\]
Therefore,\[~\Delta ACD=\Delta A+\Delta B\]
![]() Types of Triangle
Types of Triangle
Classification based on angles
Note that the other two angles are acute.
In the figure \[\angle A,\angle B\]and \[\angle C\]are acute angles.
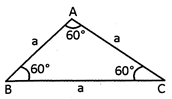
![]() Equilateral Triangle
Equilateral Triangle
A triangle in which all sides are equal is known as equilateral triangle.
![]() Isosceles Triangle
Isosceles Triangle
A triangle in which any two sides are equal is said to be and isosceles triangle.
The angles opposite to the equal sides are equal.
In the triangle given below, sides AB and AC are equal as well as \[\angle B\]and \[\angle C\]are also equal.

![]() Scalene Triangle
Scalene Triangle
A triangle in which all side are unequal is said to be scalene triangle.
In scalene triangle all angles are different.
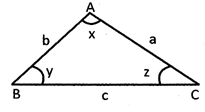
In the above given triangle all the sides of triangle denoted by a, b and c are unequal and angles x, y and z are also unequal.
![]() Pythagoras Theorem
Pythagoras Theorem
In a right angled triangle, the square of the hypotenuse is equal to the sum of the square of the other two sides, mathematically from figure,
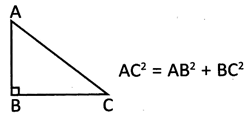
![]()
In right angled triangle AB = 3 unit, BC = 4 unit then AC equal to

(a) 3 unit
(b) 4 unit
(c) 5 unit
(d) 6 unit
(e) None of these
Answer: (c)
Explanation
We know that from Pythagoras theorem
\[A{{B}^{2}}+B{{C}^{2}}=A{{C}^{2}}{\Rightarrow }A{{C}^{2}}=\]\[{{3}^{2}}+{{4}^{2}}{\Rightarrow }9+16=25={{5}^{2}}{\Rightarrow }AC=5unit.\]
Converse of Pythagoras Theorem
If the square of one side of a triangle is equal to the sum of the square of other two sides then the triangle is right angled triangle, where right angle is opposite to the greatest side.
If in a triangle \[PQR,\text{ }P{{Q}^{2}}=P{{R}^{2}}+Q{{R}^{2}}\]then the angle opposite to PQ is right angle.
![]() Pythagorean Triplets
Pythagorean Triplets
Three integers p, q and r (such that p > q > r) are said to be a Pythagorean triplet, if \[{{p}^{2}}={{q}^{2}}+{{r}^{2}}\]

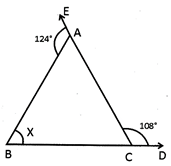
![]() In the adjoining figure, BC is produced to D and CA is produced to E, and \[\angle DCA=108{}^\circ \]and \[\angle EAB=124{}^\circ \]then the value of \[x\] is:
In the adjoining figure, BC is produced to D and CA is produced to E, and \[\angle DCA=108{}^\circ \]and \[\angle EAB=124{}^\circ \]then the value of \[x\] is:
(a) 48°
(b) 52°
(c) 76°
(d) 128°
(e) None of these
Answer: (b)
Explanation
\[\angle ACB=180{}^\circ -\angle ACD\]
\[\Rightarrow {{180}^{0}}-{{108}^{0}}={{72}^{0}}\Rightarrow \angle BAC={{180}^{0}}-EAB\]
\[\Rightarrow 180{}^\circ -124{}^\circ =56{}^\circ .\]From \[\angle ABC,\]we have
\[\Rightarrow x+(\angle ACB+\angle BAC)=\]\[{{180}^{0}}\Rightarrow x+({{72}^{0}}+{{56}^{0}})={{180}^{0}}\]
\[\Rightarrow x=180{}^\circ -128{}^\circ =52{}^\circ \]
![]() If the angles of a triangle are in the ratio 1:1:2 then which one of the following statements is incorrect?
If the angles of a triangle are in the ratio 1:1:2 then which one of the following statements is incorrect?
(a) Triangle is right angled triangle
(b) The angles of the triangles are \[90{}^\circ ,\text{ }45{}^\circ \] and\[~45{}^\circ ~\]
(c) The angles of the triangles are \[90{}^\circ ,\text{ }45{}^\circ \] and \[45{}^\circ .\]Triangle is right angled isosceles triangle.
(d) The angles of the triangles are \[90{}^\circ ,\text{ }45{}^\circ \] and \[45{}^\circ .\] And it is scalene.
(e) None of these
Answer: (d)
Explanation
The angles of triangle are \[x,\text{ }x\]and \[2x\] therefore, from angle sum property of triangle we get \[x+x+2x=180{}^\circ \] or, \[4x=180{}^\circ \]
or \[x=45{}^\circ ,\]the other angles of the triangle are \[90{}^\circ ,\text{ }45{}^\circ \] and \[45{}^\circ .\]
Here two angles are equal. Therefore, the given triangle is isosceles triangle.
![]() If the bisector of an angle of a triangle is also the median of the triangle then the triangle in which this condition is not possible?
If the bisector of an angle of a triangle is also the median of the triangle then the triangle in which this condition is not possible?
(a) Equilateral
(b) Isosceles
(c) Equiangular
(d) Scalene
(e) None of these
Answer: (c)
![]() If CE is parallel to DB in the given figure then value of \[x\] will be____.
If CE is parallel to DB in the given figure then value of \[x\] will be____.
(a) \[45{}^\circ \]
(b) \[75{}^\circ \]
(c)\[30{}^\circ \]
(d) \[85{}^\circ \]
(e) None of these
Answer: (d)
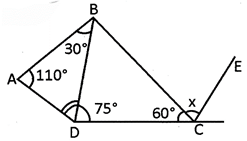
![]()
\[\angle BDC=75{}^\circ -40{}^\circ =35{}^\circ \]
\[DB\left| \text{ } \right|CE\]
\[\therefore 35{}^\circ +\left( 600+x{}^\circ \right)=180{}^\circ \]
\[\Rightarrow x=85{}^\circ \]
![]() In the given figure P is the point on side BC. Which one of the following is correct?
In the given figure P is the point on side BC. Which one of the following is correct?

(a) \[(AB+BC+CA)<2AP\]
(b) \[(AB+BC+CA)>2AP\]
(c)\[(AB+BC+CA)<AP\]
(d) \[~(AB+BC+CA)>AP\]
(e) None of these
Answer: (b)
![]()
(i) acute angled triangle
(ii) right angled triangle
(iii) obtuse angled triangle.
(i) equilateral triangle
(ii) isosceles triangle
(iii) scalene triangle.

You need to login to perform this action.
You will be redirected in
3 sec
