7th Class Mathematics The Triangle and its Properties Triangles

Triangles

• A triangle is a simple closed figure bounded by three line segments. It has three vertices three sides and three angles. The three sides and three angles of a triangle are called its six elements. It is denoted by the symbol A.

            In\[\Delta \]ABC. Sides: \[\overline{AB}\,,\overline{BC}\,and\,\overline{CA}\]; Angles:

            \[\angle \]BAC,\[\angle \]ABC and \[\angle \]BCA ; Vertices: A, Band C

• A triangle is said to be

            (a) an acute angled triangle, if each one of its

            (b) a right angled triangle, if any one of its angles measures \[{{90}^{o}}\].

            (c) an obtuse angled triangle, if any one of its angles measures more than \[{{90}^{o}}\]

            Note:    A triangles cannot have more than one right angle.

            A triangles cannot have more than one abuts angle.

            In a right triangle, the sum of the acute angles is \[\mathbf{9}{{\mathbf{0}}^{\mathbf{o}}}\]

• Angle sum property: The sum of the angles of a triangle is \[{{180}^{o}}\].
• Properties of sides:

            (i) The sum of any two sides of a triangle is greater than the third side.

            (ii) The difference of any two sides is less than the third side.

            (iii) Property of exterior angles: If a side of a triangle is produced, the exterior angle so formed

            is equal to the sum of interior opposite angles.

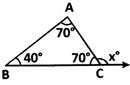
e.g., Exterior angle,

            \[{{x}^{o}}=\angle A+\angle B={{70}^{o}}+{{40}^{o}}=\,{{110}^{o}}\]

• A triangle is said to be

            (a) an equilateral triangle, if all of its sides are equal.

            (b) an isosceles triangle, if any two of its sides are equal.

            (c) a scalene triangle, if all of its sides are of different lengths.

• The medians of a triangle are the line segments joining the vertices of the triangle to the midpoints of the opposite sides.

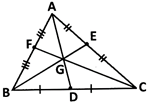
Here AD, BE and CF are medians of \[\Delta \]ABC.                      

• The medians of a triangle are concurrent.
• The centroid of a triangle is the point of concurrence of its medians. The centroid is denoted by G.
• Triangle divides the medians in the ratio 2:1.
• The medians of an equilateral triangle are equal.
• The medians to the equal sides of an isosceles triangle are equal.
• The centroid of a triangle always lies in the interior of the triangle.

• Altitudes of triangle are the perpendiculars drawn from the vertices of a triangle to the opposite sides.

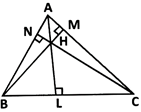
Here AL, BM and CN are the altitudes of \[\Delta \]ABC.

            The altitudes of a triangle are concurrent,       

• The orthocenter is the point of concurrence of the altitudes of triangle. Orthocenter is denoted by H.
• The orthocenter of an acute angled triangle lies in the interior B of the triangle.
• The orthocentre'of a right angled triangle is the vertex containing the right angle.
• The orthocenter of an obtuse angled triangle lies in the exterior of the triangle.

• Properties:

            (i) The altitudes drawn on equal sides of an isosceles triangle are equal.

            (ii) The altitude bisects the base of an isosceles triangle.

            (iii) The altitudes of an equilateral triangle are equal.

            (iv) The centroid of an equilateral triangle coincides with its orthocenter.

• In a right angled triangle, the side opposite to the right angle is called the hypotenuse and the other two sides are known as its legs.

• Pythagoras ‘Theorem:

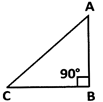
            In a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the remaining two sides.

• In the right angled triangle

            \[\operatorname{ABC}, A{{C}^{2}} = A{{B}^{2}}+B{{C}^{2}}.\]

• In a right angled triangle, the hypotenuse is the longest side.