Algebra
Category : 7th Class
Algebra
Learning Objectives
Ratio and Proportion
Ratio
We often have to compare quantities in our daily life. They may be heights, weights, salaries, marks etc. While comparing salaries of two persons i.e., salaries 6000 per month and 9000 per month, they may be written as the ratio 6000:9000 or 2 : 3. In general, the ratio of two quantities a and b in the same units is the fraction \[\frac{a}{b}\] and we write it as a:b. In the ratio a: b, we call a as the first term or antecedent and b, the second term or consequent. For example, the ratio 5:9 represents \[\frac{5}{9}\] with antecedent = 5, consequent = 9.
Note: The multiplication or division of each term of a ratio by the same non-zero number does not affect the ratio. For example, 4 : 5 = 8 : 10 = 12 : 15. Also, 4 : 6 = 2 : 3.
Proportion
The equality of two ratios is called proportion. If a : b = c : d, we write a : b :: c : d and we say that a, b, c, d are in proportion. Here a and d are called extremes, while b and c are called mean terms.
Product of means = Product of extremes.
Thus, \[a:b::c:d\Leftrightarrow (b\times c)\,\,=\,\,(a\times d)\].
Fourth Proportional: If a : b = c : d, then d is called the fourth proportional to a, b, c.
Third Proportional: a : b = c : d, then c is called the third proportion to a and b.
Mean Proportional: Mean proportional between a and b is ab.
Comparison of Ratios
We say that (a : b) > (c : d) \[\Leftrightarrow \]\[\,\frac{\mathbf{a}}{\mathbf{b}}\,\,\mathbf{>}\,\,\frac{\mathbf{c}}{\mathbf{d}}\].
Compounded Ratio: The compounded ratio of the ratios: (a : b), (c : d), (e : f) is (ace : bdf).
Duplicate Ratios:
Duplicate ratio of (a : b) is\[\left( {{a}^{2}}:\text{ }{{b}^{2}} \right)\].
Sub-duplicate ratio of (a : b) is \[\left( \sqrt{a},\text{ }\sqrt{b} \right)\] .
Triplicate ratio of (a : b) is \[\left( {{a}^{3}}:\text{ }{{b}^{3}} \right)\].
Sub-triplicate ratio of (a : b) is \[\left( {{a}^{1/3}}:\text{ }{{b}^{1/3}} \right)\].
If\[\,\,\frac{a}{b}\,\,=\,\,\frac{c}{d},\,\,then\,\,\frac{a+b}{c-b}\,\,=\,\,\frac{c+d}{c-d}\] [componendo and dividend].
Example
If 4x + 3y : 6x + 5y = \[\frac{\mathbf{11}}{\mathbf{17}}\], then find x : y.
(a) 0 : 1 (b) 2 : 1
(c) 1 : 0 (d) 5 : 0
(e) None of these
Ans. (b)
Explanation: \[\frac{4x+3y}{6x+5y}=\frac{11}{17}\,\,\,\,\Rightarrow \,\,\,\,\,17(4x+3y)\,\,\,\,=\,\,\,11(6x+5y)\]
\[~\Rightarrow \,\,\,\,\,68x + 51y = 66x + 55y\,\,\,\Rightarrow \,\,\,68x - 66x = 55y - 51y\]
\[\Rightarrow \] 2x = 4y \[\Rightarrow \]\[\frac{x}{y}\,\,=\,\,\frac{4}{2}\,\,\,\Rightarrow \] x : y = 2 : 1.
If A, B, C, D are quantities of same kind and the ratio of A to B is 3 : 4, B to C is 5 : 7 and C to D is 8:
Which one of the following options is correct?
(a) 1, 2 and 3 (b) 1 and 2
(c) 2 and 3 (d) 1 and 5
(e) None of These
Ans. (a)
Explanation: \[\frac{A}{B}=\frac{3}{4},\,\,\frac{B}{C}=\frac{5}{7}\,\,\And \,\,\frac{C}{D}=\frac{8}{9}\,\,\,\Rightarrow \,\,\,A=\frac{3}{4}B\,\,\And \,\,B=\frac{5}{7}C\,\,\,\Rightarrow \,\,A=\frac{3}{4}\times \frac{5}{7}C\,\,\,or\frac{A}{C}=\frac{15}{28}\]
\[\Rightarrow C=\frac{8}{9}D\,\,\,\,\Rightarrow \,\,\,\,B=\frac{5}{7}\times \frac{8}{9}D\,\,\,\,\Rightarrow \,\,B=\frac{40}{63}D\,\,\,\,or\,\frac{B}{D}=\frac{40}{63}\]
\[\Rightarrow \,\,A=\frac{3}{4}B=\frac{3}{4}\times \frac{40}{63}D\,\,\,=\frac{10}{21}D\,\,\,\,\,\Rightarrow \,\,\frac{A}{D}=\frac{10}{21}\] .
The ratio between two quantities is 7 : 9. If the first quantity is 511, then find the other quantity.
(a) 655 (b) 555
(c) 657 (d) 656
(e) None of these
Ans. (c)
Let the other quantity be x then
\[7:9\,\,=\,\,511:x\,\,\,\,\Rightarrow \,\,x=\frac{511\,\,\times \,\,9}{7}\,\,=\,\,657\]
Find two numbers so that their mean proportional is 14 and their proportional is 112.
(a) 6 and 27 (b) 7 and 28
(c) 9 and 29 (d) 10 and 30
(e) None of these
Ans. (b)
Let the number be x and y, then according to question
\[\sqrt{xy}\,\,=\,\,14\,\,\,\,\Rightarrow \,\,xy\,\,\,=\,\,196\,\,\,..........(i)\]
\[\Rightarrow \,\,\,\frac{x}{y}=\frac{y}{112}\,\,\,\Rightarrow \,\,{{y}^{2}}\,\,=\,\,112x\,\,\,\,...........(ii)\]
\[from\,\,(i)\,\,y=\,\,\frac{196}{x}\,\,\,\Rightarrow \,\,\frac{{{(196)}^{2}}}{{{x}^{2}}}\,\,=\,\,112x\]
\[\Rightarrow \,\,\,{{x}^{3}}=343\,\,\,\Rightarrow \,\,x=7\,\,\,and\,\,y=\frac{196}{7}\,\,=\,\,\,28\]
Hence, the required numbers are 7 and 28.
Percentage
For example, \[\frac{1}{4}=~\frac{1}{4}x\,\text{ }100%\text{ }=\text{ }25%\] whereas, \[75%=\text{ }\frac{75}{100}\,\,\,=\,\,\,\frac{3}{4}\text{ }\].
Example
Due to reduction of \[6\frac{1}{4}\]% in the price of sugar, a man is able to buy 1 kg more sugar for Rs. 120. The reduced rate of sugar is:
(a) Rs. 8 per kg (b) Rs. 6.5 per kg
(c) Rs. 7.5 per kg (d) Rs. 9 per kg
(e) None of these
Ans. (c)
Explanation: Suppose original rate of sugar be Rs. x per kg.
Reduced rate \[=\left[ \left( 100-\frac{25}{4} \right)\times \,\,\frac{1}{100}\,\,\times \,\,x \right]\,\,=\,\,\frac{15x}{16}\]
According to question, \[\frac{120}{\frac{15x}{16}}-\frac{120}{x}=1\,\,=\,\,8\,\,\Rightarrow \,\,\frac{128}{x}-\frac{120}{x}=1\,\,\,\,\Rightarrow x=8\]
Reduced rate = \[\frac{15}{16}\times 8\] = Rs. 7.5 per kg.
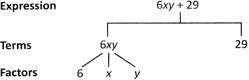
Algebraic Expressions
Algebraic expressions are formed from variables and constants. The various parts of algebraic expressions are shown below in the diagram.
Some important algebraic identities are
These identities can be used for expanding an algebraic expansion as well as to factorise the given algebraic expression.
Example
Find the value of
\[\mathbf{4xy}\text{ }\left( \mathbf{x}\text{ }-\text{ }\mathbf{y} \right)\text{ }-\text{ }\mathbf{6}{{\mathbf{x}}^{\mathbf{2}}}\left( \mathbf{y}\text{ }-\text{ }{{\mathbf{y}}^{\mathbf{2}}} \right)\text{ }-\text{ }\mathbf{3}{{\mathbf{y}}^{\mathbf{2}}}\left( \mathbf{2}{{\mathbf{x}}^{\mathbf{2}}}-\text{ }\mathbf{x} \right)\text{ }\mathbf{4}-\text{ }\mathbf{2xy}\text{ }\left( \mathbf{x}\text{ }-\text{ }\mathbf{y} \right)\text{ }\mathbf{for}\text{ }\mathbf{x}\text{ }=\text{ }\mathbf{5}\text{ }\mathbf{and}\text{ }\mathbf{y}\text{ }=\text{ }\mathbf{13}.\]
(a) -195 (b) 2535
(c) -2535 (d) 215
(e) None of these
Ans. (c)
\[4xy \left( x - y \right) - 6{{x}^{2}}\left( y - {{y}^{2}} \right) - 3{{y}^{2}}\left( 2{{x}^{2}}- x \right) + 2xy \left( x - y \right)\]
\[4{{x}^{2}}y - 4x{{y}^{2}}- 6{{x}^{2}}y + 6{{x}^{2}}{{y}^{2}}- 6{{y}^{2}}{{x}^{2}}+ 3x{{y}^{2}}+ 2{{x}^{2}}y - 2x{{y}^{2}}\]
After simplification, we get
\[-\,3x{{y}^{2}}= - 3 5 13 13 = - 2535\]
The expanded form of \[{{\left( \mathbf{2x}+\mathbf{3y}-\mathbf{5z} \right)}^{\mathbf{2}}}\] is:
(a) \[4{{x}^{2}}+ 9{{y}^{2}}+ 25{{z}^{2}}+ 12xy - 30yz - 20zx\]
(b) \[5{{x}^{2}}- 6{{y}^{3}}+ 15{{z}^{3}}+ 12xy - 36{{y}^{6}}+ 21x{{y}^{2}}\]
(c) \[8{{a}^{2}}+{{a}^{3}}- {{c}^{2}}+ 7{{x}^{2}}+ 2{{c}^{2}}+ 9{{c}^{2}}y\]
(d)\[1{{z}^{2}}- {{z}^{4}} {{8}^{C}}- 7{{5}^{2}}+ 2{{c}^{2}}- 98{{c}^{2}}\]
(e) None of these
Ans. (a)
Explanation: \[{{\left( 2x + 3y - 5z \right)}^{2}}= {{\left( 2x \right)}^{2}}+{{\left( 3y \right)}^{2}}+{{\left( - 5z \right)}^{2}}+2\left( 2x \right)\left( 3y \right) + 2\left( 3y \right)\left( - 5z \right) + 2\left( 5z \right)\left( 2x \right) = 4{{x}^{2}}+ 9{{y}^{2}}+ 25{{z}^{2}}+\]
\[12xy - 30yz - 20zx .\]
Factorize: \[{{\left( \mathbf{5a}\text{ }+\text{ }\mathbf{4b} \right)}^{\mathbf{2}}}-\text{ }{{\left( \mathbf{3a}\text{ }-\text{ }\mathbf{2b} \right)}^{\mathbf{2}}}\]
(a) \[4 \left( a + 3b \right) \left( 4a + b \right)\]
(b) \[2 \left( a + 3b \right) \left( 4a + b \right)\]
(c) \[3 \left( a + 3b \right) \left( 4a + b \right)\]
(d) \[\left( a + 3b \right) \left( 4a + b \right)\]
(e) None of these
Ans. (a)
Explanation: \[{{\left( 5a + 4b \right)}^{2}}- {{\left( 3a - 2b \right)}^{2}}\]
\[= \left[ \left( 5a + 4b \right) - \left( 3a - 2b \right) \right] \left[ \left( 5a + 4b \right) + \left( 3a - 2b \right) \right]\]
\[= \left( 2a + 6b \right)\left( 8a +2b \right)\]
\[= 2\left( a + 3b \right) 2\left( 4a + b \right)\]
\[= 4\left( a + 3b \right)\left( 4a + b \right).\]
Simple Equations
Example
Which one of the following options is the solution of the equation\[\frac{\mathbf{4x-3}}{\mathbf{2x+3}}\,\,\mathbf{=}\,\,\frac{\mathbf{5}}{\mathbf{7}}\]?
(a) 2 (b) 4
(c) 10 (d) 9
(e) None of these
Ans. (a)
Explanation: \[\frac{4x-3}{2x+3}\,\,=\,\,\frac{5}{7}\]
Multiplying both sides of the above equation by (2x + 3)
\[\frac{4x-3}{2x+3}\times \left( 2x\text{ }+\text{ }3 \right)\text{ }=\text{ }\frac{5}{7}\times \left( 2x\text{ }+\text{ }3 \right)\]
\[\Rightarrow 4x-3=\frac{5}{7}(2x+3)\,\,\,\,\Rightarrow 4x-3=\frac{10x+15}{7}\,\,\,\Rightarrow 7(4x-3)=10x+15\]
\[\Rightarrow \,\,\,28x-21=10x+15\,\,\,\,\Rightarrow 28x-10x=15+21\,\,\,\Rightarrow 18x=36\Rightarrow \,\,\,x=\frac{36}{18}=2.\]
The denominator of a rational number is greater than its numerator by 6. If the numerator is increased by 5 and the denominator is decreased by 3 then the number obtained is\[\frac{\mathbf{5}}{\mathbf{4}}\], find the rational number.
(a) \[\frac{5}{11}\] (b) \[\frac{11}{5}\]
(c) \[\frac{12}{3}\] (d) \[\frac{9}{8}\]
(e) None of these
Explanation: Let the numerator of the rational number be x.
Then the denominator of the rational number will be x + 6.
It is given that the numerator and denominator of the number are increased and decreased by 5 and 3 respectively then the number obtained is\[\frac{5}{4}\].
\[\therefore \] Numerator of the new rational number \[=\,\, x + 5.\]
Denominator of the new rational number \[= \left( x + 6 \right) - 3 = x + 3.\]
New rational number = \[\frac{x+5}{x+3}\]
But the new rational number is given as\[\frac{5}{4}\].
\[\frac{x+5}{x+3}=\,\,\frac{5}{4}\,\,\,\Rightarrow \,\,4(x+5)=5(x+3)\](By cross-multiplication)
\[\Rightarrow \] \[4x + 20 = 5x + 15.\]
\[4x - 5x = 15 - 20\] [transposing 5x to LH.S. and 20 to R.H.S.
\[\Rightarrow \,\,-x=-5\,\,or\,\,x\,\,=\,\,5\]
\[\therefore \] Numerator of the rational number = 5.
Denominator of the rational number \[= 5 + 6 = 11.\]
\[\therefore \] The required rational number =\[\frac{5}{11}\]
Exponents
The exponent of a number denotes how many times to use the number in multiplication. For example, 103. Here ‘3’ means to use 10 thrice in multiplication.
So, 10,000 = 104 (can be read as 10 raise to power 4).
We can also say that 10,000 is the 4th power of 10.
Exponents follow some laws which are as under.
For any non-zero integers a and b and whole number m and n.
(a) \[{{a}^{m}}\,\,\times \text{ }{{a}^{n}}\,\,=\text{ }{{a}^{m~+\text{ }n}}~~~~~~~~~~~~~~~~~~~\]
(b) \[{{a}^{m}}\,\,\div \text{ }{{a}^{n}}\,\,=\text{ }{{a}^{m~-\text{ }n}}~,m\,\,>\,\,n~~~~~~~~~~~~~~~~~\]
(c) \[{{({{a}^{m}})}^{n}}\,\,=\,\,{{a}^{mn}}\]
(d) \[{{a}^{m}}\,\,\times \text{ }{{b}^{m}}\,\,=\text{ (}ab{{)}^{m}}~~~~~~~~~~~~~~~~\]
(e) \[{{a}^{m}}\,\,\div \text{ }{{b}^{m}}\,\,=\text{ }{{\left( \frac{a}{b} \right)}^{m~\text{ }}}~~~~~~~~~~~~~~~~~~\] \[\left( f \right)\text{ }{{a}^{0}}=\text{ }1\]
(g) \[{{(-1)}^{even\,\,number}}\,\,=1;\,{{(-1)}^{odd\,\,number}}\,\,\,=-1\]
Example
Evaluate:
\[\frac{{{\mathbf{(27)}}^{\frac{\mathbf{-2}}{\mathbf{3}}}}\mathbf{\times (81}{{\mathbf{)}}^{\frac{\mathbf{5}}{\mathbf{4}}}}}{{{\left( \frac{\mathbf{1}}{\mathbf{3}} \right)}^{\mathbf{-3}}}}\]
(a) 1 (b) 2
(c) 3 (d) 4
(e) None of these
Ans. (a)
Explanation:
\[\frac{{{(27)}^{\frac{-2}{3}}}\times {{(81)}^{\frac{5}{4}}}}{{{\left( \frac{1}{3} \right)}^{-3}}}=\frac{{{3}^{\cancel{3}\times \left( \frac{2}{\cancel{3}} \right)}}\times {{3}^{\cancel{4}\times \frac{5}{\cancel{4}}}}}{{{3}^{3}}}=\frac{{{3}^{-2}}\times {{3}^{5}}}{{{3}^{3}}}=\frac{{{3}^{-2+5}}}{{{3}^{3}}}=\frac{{{3}^{3}}}{{{3}^{3}}}\,\,=\,\,1\]
Find the value of x so that \[{{\mathbf{2}}^{\mathbf{2x}+\mathbf{1}}}=\text{ }{{\mathbf{4}}^{\mathbf{2x}-\mathbf{1}}}\]
(a) 1 (b) 2
(c) \[\frac{3}{2}\] (d) \[\frac{1}{2}\]
(e) None of these
Ans. (c)
Explanation: We have \[{{2}^{2x+1}}={{2}^{2(2x-1)}}^{\,\,}\Leftrightarrow \,\,{{2}^{2x+1}}^{{}}=\,\,{{2}^{4x-2}}\]
\[\therefore \,\,\,2x\text{ }+\text{ }1=4x-2\text{ }\Rightarrow \text{ }2x\text{ }-\text{ }4x\text{ }=\text{ }-\text{ }2\text{ }-\text{ }1\]
\[{{=}^{{}}}-2x=-3\,\,\,\,\,\,\,\Rightarrow \,\,2x=3\,\,\,\,\Rightarrow \,\,x=\frac{3}{2}\]
You need to login to perform this action.
You will be redirected in
3 sec
