Geometry
Category : 7th Class
Geometry
Learning Objectives
Lines and Angles
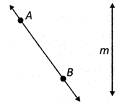
A line can be named either using two points on the line (for example\[\overleftrightarrow{AB}\] ) or simply by a letter, usually lowercase (for example, line m).
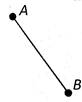
A segment is named by its two endpoints, for example \[\overline{AB}\].

A ray is named using its endpoint first, and then any other point on the ray (for example,\[\overline{BA}\])
When two lines l and m meet, we say they intersect; the meeting point is called the point of intersection.
(i) When two lines intersect (looking like the letter X), two pairs of opposite angles are formed. They are called vertically opposite angles. They are equal in measure.
(ii) A transversal is a line that intersects two or more lines at distinct points, it gives rise to several types of angles as shown in the figure.
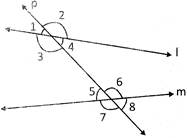
(iii) In the figure, transversal p intersects the lines I and m.
(iv) When a transversal cuts two parallel lines as shown in the figure, following relationships can be derived:

Example
In the following figure \[\mathbf{AB}\parallel \mathbf{CD}\] and LM is transversal line for AB and CD
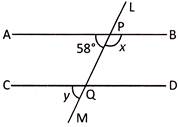
The values of x and y are respectively
(a) \[32{}^\circ , 58{}^\circ \] (b) \[122{}^\circ 58{}^\circ \]
(c) \[58{}^\circ , 122{}^\circ \] (d) \[58{}^\circ , 32{}^\circ \]
(e) None of these
Ans. (b)
Explanation: In the figure x and 58° forms a linear pair.
\[\therefore \] \[\operatorname{x}{}^\circ + 58{}^\circ = 180{}^\circ \]
\[\Rightarrow \]\[\operatorname{x}{}^\circ = 180{}^\circ - 58{}^\circ = 112{}^\circ \]
Now \[\angle \]APQ and \[\angle \]CQM are corresponding angles. Thus,
\[\angle \operatorname{CQM} =\angle APQ = 58{}^\circ \]
\[\Rightarrow \] \[\operatorname{y}{}^\circ = 58{}^\circ \]
So, option (b) is correct choice.
In the given figure, if POQ is a straight line then x is equal to:
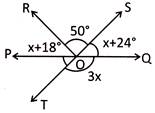
(a) \[144{}^\circ \] (b) \[145{}^\circ \]
(c) \[44{}^\circ \] (d) \[50{}^\circ \]
(e) None of these
Ans. (c)
Explanation: \[\operatorname{x} + 18{}^\circ + 50{}^\circ + x + 24{}^\circ = 180{}^\circ \]
\[\Rightarrow \] \[2x + 92{}^\circ = 180{}^\circ = 2x = 180{}^\circ - 92{}^\circ \]
\[\Rightarrow \]\[2x = 88{}^\circ ~\Rightarrow x = 44{}^\circ .\]
Triangle
\[{{\left( Hypotenuse \right)}^{2}}=\text{ }{{\left( Sid{{e}_{1}} \right)}^{2}}+\text{ }{{\left( Sid{{e}_{1}} \right)}^{2}}\]
This property does not hold good for triangles other than right angled triangle.
Example
In the adjoining figure, BC is produced to D and CA is produced to E, and \[\angle \]ACD = 108° and \[\angle \]BAE = 124°, then the value of x is:
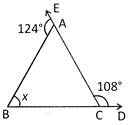
(a) \[48{}^\circ \] (b) \[52{}^\circ \]
(c) \[76{}^\circ \] (d) \[128{}^\circ \]
(e) None of these
Ans. (b)
Explanation: \[\angle \operatorname{ACB} = 180{}^\circ -\angle ACD\]
\[\Rightarrow \]\[180{}^\circ - 108{}^\circ = 72{}^\circ \,\,~\Rightarrow \,\angle \,BAC = 180{}^\circ -\angle EAB\]
\[\Rightarrow \] \[180{}^\circ - 124{}^\circ = 56{}^\circ \]
From \[\Delta \]ABC, we have
\[\Rightarrow \]\[\operatorname{x} + (\angle ACB +\angle BAC)=180{}^\circ ~\,\,\Rightarrow \,\,\,x + \left( 72{}^\circ - 56{}^\circ \right) = 180{}^\circ \]
\[\Rightarrow ~x = 180{}^\circ 128{}^\circ = 52{}^\circ \]
If the angles of a triangle are in the ratio 1: 1: 2, then which one of the following statements is incorrect?
(a) The given triangle is right angled triangle.
(b) The angles of the triangles are\[90{}^\circ , 45{}^\circ and 45{}^\circ \].
(c) The angles of the triangles are \[90{}^\circ , 45{}^\circ and 45{}^\circ \] and it is right-angled isosceles triangle.
(d) The angles of the triangles are \[90{}^\circ , 45{}^\circ and 45{}^\circ \] and it is scalene.
(e) None of these
Ans. (c)
Explanation: The angles of triangle are x, x and 2x therefore/ from angles sum property of triangle we get x +x + \[2x=180{}^\circ or, 4x = 180{}^\circ \]
or \[\operatorname{x} = 45{}^\circ \], the other angles of the triangle are\[90{}^\circ , 45{}^\circ and 45{}^\circ \]
Here two angles are equal. Therefore, the given triangle is isosceles triangle.
Congruency of triangles
SAS congruence of two triangles: Under a given correspondence, two triangles are congruent if two sides and the angle included between them in one of the triangles are equal to the corresponding sides and the angle included between them of the other triangle.
ASA congruence of two triangles: Under a given correspondence, two triangles are congruent if two angles and the side the side included between them in one of the triangles are equal to the corresponding angles and the side included between them of the other triangle.
Example
In the given figure, AC bisect \[\angle \]BAD and \[\angle \]BCD. Then which of the following methods can be used to prove\[\Delta \,\mathbf{ABC}\,\,\cong \,\,\Delta \,\mathbf{ADC}\]?
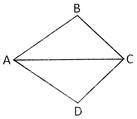
(a) Side-Angle-Side (SAS) (b) Angie-side-Angle ASA)
(c) Angle-Angle-Side (AAS) (d) Information is insufficient
(e) None of these
Ans. (b)
Explanation: In \[\Delta \]ABC and \[\Delta \]ADC,
AC = AC (common)
\[\angle \]BAC = \[\angle \]DAC (AC bisects ![]() BAD)
BAD)
\[\angle \]BCA = \[\angle \]ACD (AC bisects ![]() BCD)
BCD)
\[\therefore \,\,\,\Delta \,ABC\,\,\cong \Delta \,ADC\] by ASA congruence theorem.
Symmetry
Example
Example
How many lines of symmetry does the following figure has?
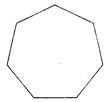
(a) 4 (b) 5
(c) 6 (d) 7
(e) None of these
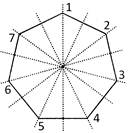
Ans. (d)
Explanation: The given figure has 7 lines of symmetry as shown below:
Which of these letter has highest order of rotational symmetry?
(a) H (b) S
(c) N (d) O
(e) None of these
Ans. (d)
Explanation: Letter O has infinite number of rotational symmetries if written circularly.
You need to login to perform this action.
You will be redirected in
3 sec
