Mensuration
Category : 7th Class
Mensuration
Learning Objectives
Mensuration
Mensuration is the branch of mathematics which deals with the study of geometrical shapes, their area, volume and related parameters. Here, we will discuss the areas and perimeter of plane figures.
Some important mensuration formula are listed in the table given below.
|
Name |
Figure |
Perimeter |
Area |
|
Rectangle |
|
\[2\left( a + b \right)\] |
\[\operatorname{a}~\,\,\times \,\,b\] |
|
Square |
|
4a |
\[{{a}^{2}}\] |
|
Right Triangle |
|
\[\operatorname{a} + b + h\] |
\[\frac{1}{2}\,\,\times \,\,a\,\,\times \,\,h\] |
|
Scalene Triangle |
|
\[\operatorname{a} + b + c\] |
\[\sqrt{s(s-a)(s-b)(s-c)}\] Where\[s=\frac{a+b+c}{2}\] |
|
Isosceles Triangle |
|
\[2a+b\] |
\[\frac{b}{4}\sqrt{4{{a}^{2}}-{{b}^{2}}}\] |
|
Equilateral Triangle |
|
3a |
\[\frac{\sqrt{3}}{4}\times {{a}^{2}}\] |
|
Parallelogram |
|
\[2\left( a +b \right)\] |
\[\left( \operatorname{a}~\,\,\times \,\,h \right)\] |
|
Rhombus |
|
4a |
\[\frac{1}{2}\,\,\times \,\,{{d}^{1}}\,\,\times \,\,{{d}^{2}}\] |
|
Trapezium |
|
Sum of all sides |
\[\frac{1}{2}\,\,\times \,\,(a+b)\,\,\times \,\,h\] |
|
Circle |
|
\[2\pi r\] |
\[\pi {{r}^{2}}\] |
Example
A girl walking at the rate of 9 km per hour crosses a square field diagonally in 12 seconds. The area of the field is: The area of the field is:
(a) 460 sq. m (b) 600 sq. m
(c) 510 sq. m (d) 450 sq. m
(e) None of these
Ans. (d)
Explanation: Distance covered by girl = \[\frac{9\times 1000}{3600}\,\,\times \,\,12\]= 30 m
So, the diagonal of square field = 30 m
Thus, the area of square field = \[\frac{1}{2}{{d}^{2}}\] (where d is diagonal)
\[=\,\,\frac{{{30}^{2}}}{2}\,\,=\,\,\frac{900}{2}\,\,\text{= }450\text{ }sq.\text{ }m.\]
The inner circumference of a circular race track which is 18 m wide is 880 m. Find the radius of the outer circle.
(a) 140 m (b) 150 m
(c) 160 m (d) 170 m
(e) None of these
Ans. (a)
Explanation: Let the inner radius be r metre.
Then \[2\pi r\,\,=\,\,640\,\,\Rightarrow \,\,2\,\,\times \,\,\frac{22}{7}\,\,\times \,\,r\,\,=\,\,880\]
\[\Rightarrow \,\,\frac{44}{7}\,\,\,r\,\,=\,\,880\,\,\,\,\Rightarrow \,\,r\,\,=\,\,880\,\,\times \,\,\frac{7}{44}\,\,=\,\,140\,m.\]
The sides of a quadrilateral taken in order are 20 cm, 27 cm, 7 cm and 24 cm. The angles between the last two sides is a right angle, find the area of quadrilateral.
(a) \[875.96\text{ }c{{m}^{2}}\] (b) \[975.50\text{ }c{{m}^{2}}\]
(c) \[375.85\text{ }c{{m}^{2}}\] (d) \[957.90\text{ }c{{m}^{2}}\]
(e) None of these
Ans. (c)
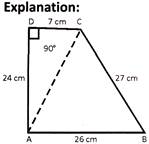
Let ABCD be a quadrilateral of sides AB = 20 cm, BC = 27 cm, CD = 7 cm,
DA = 24 cm and \[\angle CDA=\,90{}^\circ \]
Join AC, since \[\Delta \]ADC is a right angled triangle.
By using Pythagoras theorem, we have
\[{{\operatorname{AC}}^{2}}= {{7}^{2}}+ 2{{4}^{2}}= 49 + 576 = 625~\,\,\Rightarrow \,\,\,AC = 25 cm\]
Calculating area of \[\Delta \]ABC:
\[S=\frac{26+27+25}{2}=39\,cm\]
\[\therefore \,\,Area\text{ }of\,\,\Delta \,\,\,=\,\sqrt{\,39(39-26)(39-27)(39-25)}\]
= \[\sqrt{39\,\,\times \,\,13\,\,\times \,\,12\,\,\times \,\,14}\,\,=\,\,\sqrt{85,176}=291.85\,\,c{{m}^{2}}\]
Calculating area of \[\Delta \]ADC:
Area of \[\Delta \text{ }=\text{ }\frac{1}{2}\,\,\times \text{ }7\text{ }\times \text{ }24\text{ }=\text{ }84\text{ }c{{m}^{2}}\]
Area of quadrilateral ABCD = Area of \[\Delta \]ABC + Area of \[\Delta \]ADC
\[= 291.85 + 84 = 375.85 c{{m}^{2}}\].
The area of a parallelogram is \[\mathbf{70}\text{ }\mathbf{c}{{\mathbf{m}}^{\mathbf{2}}}\]and its altitude is 7 cm. Find the perimeter of a rectangle having equal area on the same base.
(a) 36 cm (b) 99 cm
(c) 79 cm (d) 34 cm
(e) None of these
Ans. (d)
Explanation: \[\operatorname{Area} of the parallelogram = base~\,\,\times \,\,\,height\]
\[\therefore \text{ }70\text{ }=\text{ }a~\,\,\times \,\,7\], where a is the base.
\[\Rightarrow \]a = 10 cm
If rectangle has one side as b cm, the base as 10 cm, the area is 70 cm2,
\[\therefore \,\,\,\,10b=70\,\,\Rightarrow \,\,b\,\,=\,\,7\,cm\]
Hence, perimeter of rectangle = 2 (10 + 7) = 34 cm.
Introduction to Solid Shapes
Oblique sketch: It is a type of sketch of the solid which does not have proportional lengths but still it conveys all important aspects of the appearance of the solid
Isometric sketch: It is a type of sketch of the solid in which the measurements are kept proportional.
Example
How many edges does a cube has?
(a) 4 (b) 6
(c) 8 (d) 12
(e) None of these
Ans. (d)
Explanation: A cube has 12 edges.
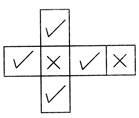
The net shown below belongs to which solid shape?
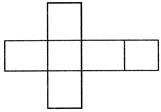
(a) Cube (b) Cuboid
(c) Rectangle (d) Cylinder
(e) None of these
Ans. (b)
Explanation: The two faces (x mark) of the net are of equal sizes while the other four (3 mark) are equal in size but different from the first two. Thus, the net belongs to cuboid.
Important Facts
You need to login to perform this action.
You will be redirected in
3 sec
