Number System
Learning Objectives
- Number Line
- Fractions and Decimals
- Rational Number
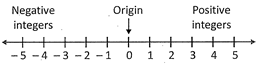
Number Line
Number line is a model that helps us visualise adding and subtracting of integers. A number line is a picture of a straight Sine on which every point is assumed to correspond to a real number and every real number to a point.
Absolute Value
Absolute value means to think only about how far a number is from zero.

For example “6” is 6 away from zero, but” -6” is also 6 away from zero. So the absolute value of 6 is 6 and the absolute value of- 6 is also 6.
Properties of addition of integer
- Commutative property: \[\left( A + B \right) = \left( B + A \right)\].
- Associative property: \[\operatorname{A} + \left( B + C \right) = \left( A + B \right) +C\].
- Additive Identity: Additive identity is any number which when added to a number N will result in the same number, i.e., N + 0 = N. Hence, 0 is the additive identity.
- Additive Inverse: Inverse identity is any number which when added to a number M will result in zero. Here, N + (-N) = 0. Hence, in general, additive inverse of N is -N.
Properties of subtraction of integer
- Commutative property does not exist for subtraction, i.e., \[2-3~\,\,\ne \,\,3-2\]
- Associative property also does not exist for subtraction, i.e., \[2-\left( 3 - 4 \right)~\ne \left( 2 - 3 \right) 4\]
- Identity property: Same as that of Additive identity. 0 + (-N) = -N, where N is positive.
- Inverse property: N is the inverse of a number -N where N is positive, since N - N = 0.
Properties of multiplication of integers
- Closure property: Integers are closed under multiplication, i.e. for any two integers, a and b, ab is an integer.
Example: \[5~\times 6 = 30; -9~\times -3 = 27\]
- Commutative property: Division is NOT commutative for integers- For any two integers a and b
Example: 3/6 = 1/2.
- Associative property: Multiplication is associative for integers. For any three integers, a, b and c, \[(a~\times b)~\times c = a~\times (b~\times c)\]
Example: \[[\left( -3 \right)~\times \left( -2 \right))\times ~4]\text{ }=\text{ }(6~\times 4)\text{ }=\text{ }24\]
Identity property: The integer 1 is the identity under multiplication. That is, for an integer a, for an integer a \[1~\times a = a~\,\times 1 = a.\]
Example: \[\left( -4 \right)~\times 1 = 1~\times \left( -4 \right) = -4\],
Under addition and multiplication, integers show a property called distribution property. That is, \[\operatorname{a}\,\times \left( b + c \right) = a~\,\times \,\,b + a\,~\times \,\,c\] for any three integers a, b and c.
Important Facts about Number System
- If the integer (-1) is multiplied even number of times, the product is +1 and if the integer (-1) is multiplied odd number of times, the product is -1. You can check this by making pairs of (-1) is multiplied odd number of times, the product is -1. You can check this by making pairs of (-1) in the statement. This is useful in working out products of integers.
- Product of a positive and a negative integer is a negative integer whereas the product of two negative integers is a positive integer For example \[- 2~\,\times \,\,7 = -14 \,and\, -3\,\,\times - 8=24\].
- Product of even number of negative integers is positive, whereas the product of odd number of negative integers is negative.
- 0 is the additive identity whereas 1 is the multiplicative identity for integers. We get additive inverse of an integer a when we multiply (-1) to a, i.e. \[\operatorname{a}\,~\times \,\,\left( -1 \right) = \left( -1 \right)~a = - a\]
- Like whole numbers, any integer divided by zero is meaningless and zero divided ban integer other than zero is equal to zero i.e., for any integer a, a \[\div \] 0 is not defined but\[0\,\,~\div \,\,a = 0 for a~\,\,\ne \,\,\,0\].
- When we divide a whole number by 1 it gives the same whole number.
Example
The sum of additive inverse of -53 and multiplicative inverse of \[\frac{\mathbf{1}}{\mathbf{47}}\] is
(a) 6 (b) -100
(c) 100 (d) -6
(e) None of these
Ans. (c)
Explanation: The additive inverse of - 53 is 53.
Similarly, the multiplicative inverse of \[\frac{1}{47}\] is 47.
Thus, the required sum = 53 + 47 = 100.
Fractions and Decimals
There is lots of space in between the two integers on a number line. This area of number line represents fractions and decimal numbers. All integers can be expressed as fractions and decimals but all fractions and decimals cannot be expressed as Integers. For example, 2 can be represented in the form of a fraction as 2/1 and in the form of decimal as 2.00 but 2.5634 cannot be expressed as an integer or a whole number
Fractions
Fractions can be mainly divided in two types - (i) proper fractions, (ii) Improper fractions or mixed fractions.
- A proper fraction is a fraction that represents a part of a whole. For example, \[\frac{2}{7},\,\,\frac{3}{8}.\]
- An improper fraction is a combination of whole and a proper fraction.
For example, \[5\,\frac{2}{3}\] and\[2\,\frac{4}{5}\]. This type of fractions are also called mixed fraction.
Decimals
The decimal numeral system has ten as its base. A decimal is a tenth part and decimals become a series of nested tenths. For example, 1.35 is a decimal number
Decimals can be divided into like decimals and unlike decimals on the basis of digits to the right of the decimal.
- Like decimals have same number of digits to the right of the decimal. For example, 23.65 and 2.83.
- The numbers that have unequal number of digits to the right of the decimal are called unlike decimals. For example, 2.354 and 0.23.
Decimals can also be divided as terminating and non-terminating decimals
- Here we consider only those divisions in which the remainder is zero.
- To divide a decimal number by a whole number, we first divide them as whole numbers. Then place the decimal point in the quotient as in the decimal number For example\[8.4~\,\,\div \,\,4 = 2.1\].
- To multiply a decimal number by 10, 100 or 1000, we move the decimal point in the number to the right by as many places as there are zeros over 1. Thus \[0.53~\,\times \,\,10 =5. 0.53~\,\,\times \,\,100 = 53, 0.53~\,\,\times \,\,1000 - 530\].
- A reciprocal of a fraction is obtained by inverting it upside down.
- The product of two improper fractions is greater than the two fractions.
- The product of a proper and an improper fraction is less than the improper fraction and greater than the proper fraction.
- The product of two proper fractions is less than each of the fractions that are multiplied.
- The decimals which do not have any end point and no repetition of digits at the right end of the decimal are called non-terminating non-repeating decimals. For example 0.4534782..., 0.54688521917....
- The decimals in which a digit or a set of digit repeats periodically are called non-terminating repeating decimals. For example, 0.2222222..., 0.3333333..., 0.45454545.
- The decimals which do not have any end at the right of the decimal are called non- terminating decimals. These are further classified into two types - (i) non-terminating repeating decimals and (ii) non-terminating non-repeating decimals.
- The decimal number which comes to an end at the right of the decimal are called terminating decimals.
- To divide a decimal number by 10,100 or 1000, shift the digits in the decimal number to the left by as many places as there are zeros over 1, to get the quotient. So, \[23.9~\div 10=2.39,\text{ }23.9~\div 100=0.239,\text{ }23.9\div ~1000=0.0239\].
- While dividing two decimal numbers, first shift the decimal point to the right by equal number of places in both, to convert the divisor to a whole number. Then divide. Thus \[2.4\,\,~\div \,\,0.2 = 24~\,\,\div \,\,2 = 12\]
Rational Number
- A rational number is any number that can be expressed as the quotient or fraction \[\frac{p}{q}\] of two integers, with the denominator q not equal to zero. It can be positive \[\left( \frac{3}{4} \right)\] or negative\[\left( -\frac{3}{4} \right)\].
- A rational number in which denominator is positive is said to be the standard form of a rational number. For example, \[\frac{3}{7},\,\,\frac{-2}{7}\] are the rational numbers that are in standard form but the rational numbers like \[\frac{-15}{-8}\]and \[\frac{15}{(-8)}\] are not in standard form.
- Equivalent rational numbers of a fraction \[\frac{p}{q}\] can be find by multiplying both the numerator and denominator with same integer.
- Rational numbers can be compared.
If the length and breadth of a rectangle are \[\frac{\mathbf{5}}{\mathbf{4}}\]m and \[\frac{\mathbf{3}}{\mathbf{16}}\]m respectively then the perimeter of the rectangle is.
(a) \[\frac{20}{23}\]m (b) \[\frac{23}{8}\]m
(c) \[\frac{8}{23}\]m (d) \[\frac{23}{20}\]m
(e) None of these
Ans. (b)
Explanation: Perimeter = 2[Length - Breadth]
\[=\,2\times \left[ \frac{5}{4}+\frac{3}{16} \right]=2\times \frac{20+3}{16}=2\times \frac{23}{16}=\frac{23}{8}\]
In a class of 80 students, \[\frac{\mathbf{4}}{\mathbf{5}}\] of the total number of students are girls. How many students of the class are boys?
(a) 64 (b) 16
(c) 75 (d) 56
(e) None of these
Ans. (b)
Explanation: Total number of students = 80
Number of girls = \[\frac{4}{5}\,\,\times \,\,80\,\,=\,\,64\]
Number of boys = 80 - 64 = 16
If \[\frac{\mathbf{43}\mathbf{.65}}{\mathbf{8}\mathbf{.79}}\mathbf{\div }\frac{\mathbf{1}}{\mathbf{x}}\mathbf{=}\frac{\mathbf{0}\mathbf{.4365}}{\mathbf{87}\mathbf{.9}}\] then value of x is:
(a) 10 (b) 0.1
(c) 0.01 (d) 0.001
(e) None of these
Ans. (d)
Explanation: Given, \[\frac{43.65}{8.79}\div \frac{1}{x}=\frac{0.4365}{87.9}\]
\[\Rightarrow \frac{43.65}{8.79}\times x\,\,=\,\,\frac{0.4365}{87.9}\]
\[\Rightarrow \,\,x\,\,=\,\,\frac{0.4365}{87.9}\,\,\div \,\,\frac{43.65}{8.79}\]
\[\Rightarrow \,\,x\,\,=\,\,\frac{0.4365}{87.9}\,\,\times \,\,\frac{8.79}{43.65}\]
\[\Rightarrow \,\,x\,\,=\,\,\frac{1}{10}\,\,\times \,\,\frac{1}{100}\,\,=\,\,0.001\]
Which of the following forms a pair of equivalent rational numbers?
(a) \[\frac{20}{40}\,\,and\,\,\frac{35}{50}\]
(b) \[\frac{-25}{35}\,\,and\,\,\frac{55}{-77}\]
(c) \[\frac{-8}{15}\,\,and\,\,\frac{-24}{48}\]
(d) \[\frac{9}{72}\,\,and\,\,\frac{-3}{21}\]
(e) None of these
Ans. (b)
Explanation:
\[\frac{24}{40}=\frac{2}{5},\frac{35}{50}=\frac{7}{10};\frac{-25}{35}=\frac{-5}{7},\frac{55}{-77}=\frac{5}{-7};\frac{-8}{15}=\frac{-8}{15},\]\[\frac{-24} {48}=\frac{-1}{2};\frac{9}{72}=\frac{1}{8},\frac{-3}{21}=\frac{-1}{7}\]
Thus, the pair of rational numbers in option (b) is of equivalent rational numbers.


