Algebraic Expressions & Identities
Category : 8th Class
ALGEBRAIC EXPRESSION & IDENTITIES
FUNDAMENTALS
In our GMO Class VII, We have learnt about the addition and subtraction of algebraic expressions.
We will carry those ideas further.
Addition of Algebraic Expressions
While adding algebraic expressions, we collect the like terms and add them.
EXAMPLE 1. Add: \[\left( 2m+3n+59\text{ }and-n-p+6q+3m \right)\]
Solution: Writing the terms of the given expressions in the same order in form of rows with like terms below each other and adding column wise, we get:
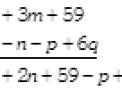
Example 2- Add: \[9{{x}^{3}}+6{{x}^{5}}-8+16{{x}^{2}}\] and \[10{{x}^{8}}6{{x}^{2}}+9{{x}^{3}}-3x\]
Solution: Writing the given expressions in descending powers of x in the form of rows with like terms below each other and adding column wise, we get:
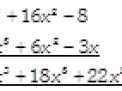
Subtraction of Algebraic Expressions
Steps:
EXAMPLE 4. Subtract \[3m+4n-5p{}^\circ \] from \[2n+8m{}^\circ +17p\]
Remember from chapter 6, Class VII, GMO that any number to the power zero is 1
\[\therefore p{}^\circ =1\]and \[m{}^\circ =1\Rightarrow 5p{}^\circ =5\]and \[8m{}^\circ =8\]
\[\therefore \] we have,
![]()
EXAMPLE 5: Subtract \[6{{x}^{2}}-3x-14\] from \[5+2x-2{{x}^{2}}+13{{x}^{3}}\]
Solution: Arranging the terms of the given expressions in descending powers of x and subtracting column wise, we get:
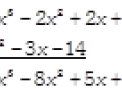
Multiplication of Algebraic Expressions
As we learnt in chapter 6, Class VII GMO Book,
Thus, \[{{2}^{3}}\times {{2}^{2}}={{2}^{5}}\]
Which you can ordinarily also verify as \[{{2}^{3}}=8;{{2}^{2}}=4;8\times 4=32={{2}^{5}}.\]
(a). Multiplication of Two Monomials
Remember, Product of two monomials = (product of their numerical coefficients) x (Product of their variable parts)
EXAMPLE-1: Find the product of:
(i) \[-7{{x}^{2}}yz\,and\,-6{{y}^{2}}zx\]
Solution:- \[-7{{x}^{2}}yz-(6{{y}^{2}}zx)\]
\[=\left\{ (-7)\times (-61) \right\}\times \left\{ {{x}^{2}}yz\times {{y}^{2}}zx \right\}\]
\[=\left\{ (-7)\times (-61) \right\}\times \left\{ {{x}^{2}}yz\times {{y}^{2}}zx \right\}\]
\[=42\times {{x}^{3}}{{y}^{3}}{{z}^{3}}\]
(b). Multiplication of a Polynomial by a Monomial
Multiple each term of the polynomial by the monomial, using the distributive law for multiplication over addition.
EXAMPLE-2 Find each of the following products:
(i) \[8{{a}^{3}}{{b}^{2}}\times \left( 6{{a}^{2}}-5ab+9{{b}^{2}} \right)\]
Solution: We have:
\[8{{a}^{3}}{{\text{b}}^{2}}\times \left( 6{{a}^{2}}-5ab+9{{b}^{2}} \right)\]
\[=\left( 8{{a}^{3}}{{b}^{2}} \right)\times \left( 6{{a}^{2}} \right)+\left( 8{{a}^{3}}{{b}^{2}} \right)\times \left( -5ab \right)+\left( 8{{a}^{3}}{{b}^{2}} \right)\times \left( 9{{b}^{2}} \right)\]
\[=48{{a}^{5}}{{\text{b}}^{2}}-40{{a}^{4}}{{b}^{3}}+72{{a}^{3}}{{b}^{4}}\]
(c). Multiplication of Two Binomials
Suppose (a + b) and (c + d) are two binomials. By using the distributive law of multiplication over addition twice, we may find their product as given below.
\[\left( a+b \right)\times \left( c+d \right)=a\times \left( c+d \right)+b\times \left( c+d \right)\]
\[=\left( a\times c+a\times d \right)+\left( b\times c+b\times d \right)\]
\[=ac+ad+be+bd.\]
This result may be remembered as it sometimes helps in quick calculations.
This method is known as the horizontal method.
EXAMPLE-3: Multiply \[\left( 8x+5y \right)\] and\[\left( 5x-6y \right)\].
Solution: We have,
\[\left( 8x+5y \right)\times \left( 5x-6y \right)\]
\[=8x\times \left( 5x-6y \right)+5y\times \left( 5x-6y \right)\]
\[=8x\times 5x-8x\times 6y+(5y\times 5x-5y\times 6y)\]
\[=\left( 40{{x}^{2}}-48xy \right)+(25xy-30{{y}^{2}})\]
\[=40{{x}^{2}}-23xy-30{{y}^{2}}\]
if we remember
\[\left( a+b \right)\times (c+d)=ac+ad+bc+bd;\] then,
\[\left( a-b \right)\left( c+d \right)=ac+ad-bc-bd\] as this result can be easily obtained from the above result by substituting b by (-b)
Column wise multiplication
The multiplication can be performed column wise as shown below.
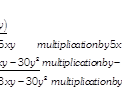
(d) Multiplication of Two Ploynomials
We may extend the above result for two polynomials, as shown below.
EXAMPLE4: first let us take two polynomials say, \[\left( {{x}^{2}}+2x+3 \right)\]and \[\left( 3{{x}^{2}}-5x-6 \right)\]
Solution:
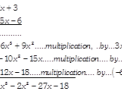
Division of Algebraic Expressions
Remember,
If x is a variable and m, n are positive integers such that m > n then \[({{x}^{m}}\div {{x}^{n}})={{x}^{m-n}}\] (This property is applicable even when m < n and m and n are any real numbers, but just to keep the matters simple, we are considering m, n > o and \[m,n\in z\]) Let us take an example \[{{x}^{3}}\div {{x}^{2}}={{x}^{3-}}^{2}={{x}^{1}}=x\]
(a). Division of a Monomial by a Monomial
Rule: Quotient of two monomials =(quotient of their numerical coefficients) \[\times \] ( quotient of their variables)
EXAMPLE 1 (i) \[6{{x}^{16}}{{y}^{7}}\,by\,(-3y6)\]
(ii) \[(-13{{x}^{8}}{{y}^{6}}{{z}^{4}})\,by\,(-2{{x}^{4}}{{y}^{2}}{{z}^{2}}{{u}^{2}})\]
Solution: We have,
(i) \[\frac{6{{x}^{16}}{{y}^{7}}}{-3{{y}^{6}}}=\left( \frac{6}{-3} \right)\times {{x}^{16}}\times {{y}^{(7-6)}}=-2{{x}^{16}}y\]
(ii) \[\frac{-13{{x}^{8}}{{y}^{6}}{{z}^{4}}}{-2{{x}^{4}}{{y}^{2}}{{z}^{2}}{{u}^{2}}}=\left( \frac{-13}{-2} \right)\times \frac{{{x}^{8-4}}{{y}^{6-2}}{{z}^{4-2}}}{{{u}^{2}}}=\frac{13{{x}^{4}}{{y}^{4}}{{z}^{2}}}{2{{u}^{2}}}\]
(b). Division of a Polynomial by a Monomial
Rule: For dividing a polynomial by a monomial, divide each term of the polynomial by the monomial.
EXAMPLE 2
(i) \[343{{x}^{8}}+49{{x}^{6}}-7\text{ }by\text{ }7{{x}^{4}}\]
(ii) \[144{{x}^{2}}{{y}^{2}}{{z}^{2}}-72{{x}^{2}}yz-18zyx\,\,\text{by}\,\,9,xyz\]
Solution: (i)
\[\frac{343{{x}^{8}}+49{{x}^{3}}-7}{7{{x}^{4}}}=\frac{343{{x}^{8}}}{7{{x}^{4}}}+\frac{49{{x}^{3}}}{7{{x}^{4}}}-\frac{7}{7{{x}^{4}}}\]
\[=\left( \frac{343}{7} \right)\times \left( \frac{{{x}^{8}}}{{{x}^{4}}} \right)+\left( \frac{49}{7} \right)\times \frac{{{x}^{3}}}{{{x}^{4}}}-\frac{1}{{{x}^{4}}};\]
\[=49\times ({{x}^{8-4}})+7\times ({{x}^{6-4}})-\frac{1}{{{x}^{4}}}\]
\[=49{{x}^{4}}+7{{x}^{2}}-\frac{1}{{{x}^{4}}}\]
(ii) \[\frac{144{{x}^{2}}{{y}^{2}}{{z}^{2}}-72{{x}^{2}}yz-18zyz}{9xyz}\]
\[=\frac{144{{x}^{2}}{{y}^{2}}{{z}^{2}}}{9xyz}-\frac{72{{x}^{2}}yz}{9xyz}-\frac{18zyx}{9xyz}\]
Since, zyx is same as xyz,
We have \[\left( \frac{144}{9} \right)\times 9\left( \frac{{{x}^{2}}{{y}^{2}}{{y}^{2}}}{xyz} \right)-\left( \frac{72}{9} \right)\times \left( \frac{{{x}^{2}}yz}{xyz} \right)-\left( \frac{18}{9} \right)\times \left( \frac{xyz}{9xyz} \right)\]
\[=16\times ({{x}^{2-1}}.{{y}^{2-1}}.{{z}^{2-1}})-8\times ({{x}^{2-1}}.{{y}^{1-1}}.{{z}^{1-1}})-2\times 1\]\[=16xyz-8x{{y}^{{}^\circ }}{{z}^{{}^\circ }}-2\]
\[=16xyz-8x-2\,(since\text{ }{{y}^{{}^\circ }}=1,{{z}^{{}^\circ }}=1)\]
(c) Division of a Polynomial by a Polynomial
Steps are as follows:
EXAMPLE 3. Divide:
\[8{{x}^{2}}-22x+15\text{ }by\text{ }\left( 4x-5 \right)\]

\[\therefore \] Quotient \[=(2x-3);\] Remainder = 0.
Now let us take example where \[R\ne 0\]but degree of remainder < degree of divisor
EXAMPLE 4. Divide \[\left( 64{{x}^{3}}-40{{x}^{2}}-4x+2 \right)\] by \[\left( 16{{x}^{2}}+2x-1 \right)\]
Solution: The terms of the dividend and the divisor are already arranged in descending order. So, we divide as follows:
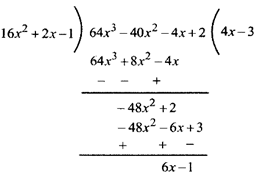
Here, Divisor \[=16{{x}^{2}}+2x-1\]
Dividend \[=64{{x}^{3}}-40{{x}^{2}}-4x+2\]
Quotient \[=4x-3\]
Remainder(R) \[=6x-1\]
We can see that Deg (R) = 1
Deg (DIVISOR) = 2; i.e. deg(R) < deg (d)
Special Identities
An identity is an equality, which is true for all values of the variables, within the set of Real numbers.
The following identities are very important.
Identity 1: \[{{\left( a+b \right)}^{2}}-{{a}^{2}}+2ab+{{b}^{2}}.\]
Proof Taking LHS,
\[{{\left( a+b \right)}^{2}}-\left( a+b \right)\left( a+b \right)\]
\[=a\left( a+b \right)+b\left( a+b \right)\] (distributive law of multiplication over addition)
\[={{a}^{2}}+ab+ba+{{b}^{2}}\]
\[={{a}^{2}}+2ab+{{b}^{2}}\] [by commutative law,\[ba=ab\]]
\[\therefore {{\left( a+b \right)}^{2}}-{{a}^{2}}+2ab+{{b}^{2}}=RHS\]
Identity 2: \[{{\left( a-b \right)}^{2}}=\left( {{a}^{2}}-2ab+{{b}^{2}} \right).\]
Proof Taking LHS,
\[{{(a-b)}^{2}}=(a-b)(a-b)=a(a-b)+b(a-b)\]
\[={{a}^{2}}-ab-ba+{{b}^{2}}\]
\[{{a}^{2}}-ab-ab+{{b}^{2}}\,\,\,\,\,[as,ba=ab]\]
\[={{a}^{2}}-2ab+{{b}^{2}}.=RHS\]
\[\therefore {{(a-b)}^{2}}=({{a}^{2}}-2ab+{{b}^{2}}).\]
Identity3: \[\left( a+b \right)\left( a-b \right)=\left( {{a}^{2}}-{{b}^{2}} \right).\]
Proof Taking LHS,
\[\left( a+b \right)\left( a-b \right)=a\left( a-b \right)+b\left( a-b \right)\]
\[={{a}^{2}}-ab+ba-{{b}^{2}}\]
\[={{a}^{2}}-ab+ab-{{b}^{2}}\]
[since \[ba=ab\]]
\[={{a}^{2}}-{{b}^{2}}=RHS\]
\[\therefore (a+b)(a-b)=({{a}^{2}}-{{b}^{2}}).\]
NOTE: We may write these identities again AND WE MUST commit them to memory.
The same identities can also be written as,
\[{{(x+y)}^{2}}={{x}^{2}}+{{y}^{2}}+2xy\]
\[{{\left( x-y \right)}^{2}}={{x}^{2}}\text{+}{{y}^{2}}-2xy\]
and \[\left( x+y \right)\left( x-y \right)=\left( {{x}^{2}}-{{y}^{2}} \right)\]
EXAMPLE 1 (i) \[{{\left( \frac{3}{2}a+\frac{3}{4}b \right)}^{2}}\]
Solution: we have,
\[{{\left( \frac{3}{2}a+\frac{3}{4}b \right)}^{2}}={{\left( \frac{3}{2}a \right)}^{2}}+{{\left( \frac{3}{4}b \right)}^{2}}+2\times \frac{3}{2}a\times \frac{3}{4}b\]
[since\[{{\left( x+y \right)}^{2}}-{{x}^{2}}+{{y}^{2}}+2xy\]]
\[=\frac{9}{4}{{a}^{2}}+\frac{9}{16}{{b}^{2}}+\frac{9}{4}ab.\]
EXAMPLE 2 (i) \[{{\left( \frac{3}{2}p-\frac{5}{3}q \right)}^{2}}\]
Solution: we have,
\[{{\left( \frac{3}{2}p-\frac{5}{3}q \right)}^{2}}={{\left( \frac{3}{2}p \right)}^{2}}+{{\left( \frac{5}{3}q \right)}^{2}}-2\times \frac{3}{2}p\times \frac{5}{3}q\]
\[=\frac{9}{4}{{p}^{2}}+\frac{25}{9}{{q}^{2}}-5pq.\]
EXAMPLE 3: Given, \[~x+\frac{1}{x}=3\] find the values of (a) \[{{x}^{2}}+\frac{1}{{{x}^{2}}}\] (b) \[{{x}^{3}}+\frac{1}{{{x}^{3}}}\] and, (c) \[{{x}^{4}}+\frac{1}{{{x}^{4}}}\]
Solution: we have,
(a)\[~x+\frac{1}{x}=3\Rightarrow {{\left( x+\frac{1}{x} \right)}^{2}}={{(3)}^{2}}\] [squaring both sides]
\[\Rightarrow {{x}^{2}}\frac{1}{{{x}^{2}}}+2\times x\times \frac{1}{2}=9\]
\[\Rightarrow {{x}^{2}}\frac{1}{{{x}^{2}}}+2=9\Rightarrow {{x}^{2}}+\frac{1}{{{x}^{2}}}=(9-2)\]
\[\therefore {{x}^{2}}\frac{1}{{{x}^{2}}}=9\]
(ii) \[{{x}^{2}}+\frac{1}{{{x}^{2}}}=7\Rightarrow {{\left( {{x}^{2}}+\frac{1}{{{x}^{2}}} \right)}^{2}}={{\left( 7 \right)}^{2}}\] [squaring both sides]
\[\Rightarrow {{x}^{4}}+\frac{1}{{{x}^{4}}}+2\times {{x}^{2}}\times \frac{1}{{{x}^{2}}}=49\]
EXAMPLE 4. Which of the following is untrue?
(a) \[{{\left( 128 \right)}^{2}}-{{\left( 72 \right)}^{2}}=11200;\]
(b) \[397\times 403=159991;\]
(c) \[\frac{198\times 198-102\times 102}{96}=202,\]
(d) \[{{(8.63)}^{2}}-{{(1.37)}^{2}}=72.6\]
Solution: \[{{\left( 128 \right)}^{2}}-{{\left( 72 \right)}^{2}}\]
The first thing that should strike you is that \[128+72=200\] is a simple rounded no.
This is:- (i) Going to make your calculation easy and
(ii) More importantly, it indicates that you have to add (128 + 72) and thus you get a way to easily calculate, as other factor will be (128-72)
[By applying the formula,
\[{{a}^{2}}-{{b}^{2}}=\left( a+b \right)\left( a-b \right)\]]
Thus, \[{{128}^{2}}-{{72}^{2}}=\left( 128+72 \right)\left( 128-72 \right)=200\times 56=11200\]Now consider, \[397\times 403.\] Here, trick is to write this as,
\[(400-3)\times (400+3)={{400}^{2}}-{{3}^{2}}=160000-9=159991\] consider, \[\frac{198\times 198-102\times 102}{96}\]; Values are indicative of the process to be carried out. 96 in the denominator indicates that some factor or multiple of 96 may be in the numerator.
So, we get,
\[\frac{\left( 198+102 \right)\times \left( 198-102 \right)}{96}=\frac{300\times 96}{96}=300\]
Lastly, \[{{\left( 8.63 \right)}^{2}}-{{\left( 1.37 \right)}^{2}}=\left( 8.63+1.37 \right)\times \left( 8.63-1.37 \right)\]\[=10\times 7.26=72.6;\]
\[\therefore \] (c) is the correct answer.
You need to login to perform this action.
You will be redirected in
3 sec
