8th Class Mathematics Practical Geometry GEOMETRY

Introduction:

The word ‘geometry originally came from the Greek word ‘geo’ meaning ‘earth’ and ‘metron’ meaning ‘measurement’. Therefore the word geometry means ‘measurement of earth’ or is the science of properties and relations of figures.

The scope of plane geometry, as a branch of mathematics, has broadened the study about plane figures-line, angles, triangles, quadrilaterals, circle, etc.

 

POINTS TO REMEMBER

• Three or more points are said to be collinear, if they lie on a line, otherwise they are said to be non-collinear.
• There are infinite number of lines passing through a given point. These lines are called concurrent lines.
• The ratio of intersects made by three parallel lines on a transversal is equal to ratio of corresponding intercept made by same parallel lines to other transversal.

         

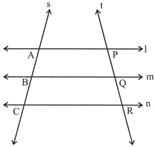
         s and t are two transversal intersecting three parallel lines 1, m and n at A, B, C and P, Q, R, respectively

         \[ABCD=\frac{1}{2}(AB+D\times CE)\]  \[\angle R={{138}^{o}}\]

 

PARALLEL LINE AND TRANSVERSAL

If a transversal P intersect two parallel lines e|| m (as shown in the figure) then,

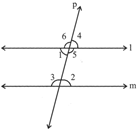
(i)   Corresponding angles are equal

\[\angle R={{138}^{o}}\]                  {corresponding angles}

\[\angle ACB={{65}^{o}}\]                  {corresponding angles}

(ii)   Alternate interior angles are equal

\[\angle ABC\]                    {alternate interior angles}

\[{{25}^{o}}\]                    {alternate interior angles}

(iii) Sum of consecutive interior angles in the same side of transversal is \[{{35}^{o}}\]

\[{{55}^{o}}\]

\[{{208}^{o}}\]

In the figure given below \[{{52}^{o}}\]

 

TRLANGLE

A triangle is a closed plane figure bound by three line segments. So, A triangle has six parts, three sides AB/BC and CA three angles \[\Delta XYZ\] and \[\Delta XYZ\]

      

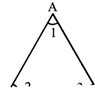
Sum of all the angles in a triangle is \[{{60}^{o}}\]

\[{{30}^{o}}\]    \[{{80}^{o}}\]

Median: The line segment joining a vertex of a triangle to the mid-point of the opposite side is called a median of the triangle.

(i) Intersecting point of the medians is called the centroid o the triangle.

(ii) Centroid divide the median in the ratio 2:1

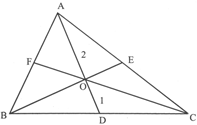
AD is the median \[{{100}^{o}}\]\[\angle DAC={{54}^{o}}\](median bisect opposite side)

AD, BE and CF are medians\[\angle ACB={{63}^{o}}\]O is centroid

So,  \[{{(2.5)}^{2}}+{{(PT)}^{2}}={{(4.5)}^{2}}\] or  \[\angle ACB={{63}^{o}}\]

 

QUADRILATERAL

A closed figure with four sides is called quadrilateral

Quadrilateral ABCD has:

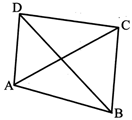
(i)   Four sides: AB,BC, CD and DA.

(ii) Four vertices: A, B,C and D.

(iii) Four angles: \[{{(PT)}^{2}}=20.25-6.25=14\] and \[{{(PT)}^{2}}=PA\times PB\].

(iv) Two diagonals: AC and BD.

Properties of Quadrilateral

• A quadrilateral is convex, if for any side of the quadrilateral, the lines containing it has the remaining vertices on the same side of it.
• The sum of the angles of a quadrilateral is \[PB=x\].
• If the sides of a quadrilateral are produced, in order, the sum of the four exterior angles so formed is \[\therefore \]

 

TYPES OF QUADRILATERAL

 

TRAPEZUM

A quadrilateral in which one pair of opposite sides are parallel is called trapezium.

In quadrilateral (ABCD), \[PA=(x+3)\]

Thus,  ABCD is a trapezium.

 

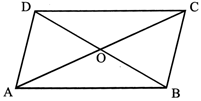
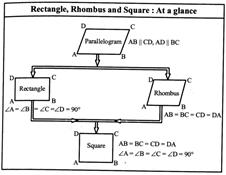
PARALLELOGRAM

A quadrilateral with both pair of opposite sides are parallel is called a parallelogram.

Properties of Parallelogram

• Opposite sides of a parallelogram are equal.
• Opposite angles of a parallelogram are equal.
• Diagonals of a parallelogram bisect each other.

 

• ABCD is a parallelogram, then

     (i) \[14=(x+3)x\]

     (ii) \[\Rightarrow \]

     (iii) \[{{x}^{2}}+3x-14=0\]

     (iv) \[\Rightarrow \]

 

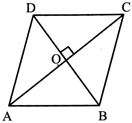
RHOMBUS

A parallelogram with a pair of adjacent sides are equal is called a rhombus.

Properties of Rhombus: All the sides of a rhombus are equal

• \[x=\frac{-3\pm \sqrt{65}}{2}\]is a rhombus \[\therefore \] AB=BC=CD=AD

OA = OC

OB = OD

Diagonals of a rhombus bisects each other at \[PB=x=\frac{-3\pm \sqrt{65}}{2}=\frac{-3+8.06}{2}=2.53\]

• A parallelogram with each angle as right angle is called a rectangle.

Properties of Rectangle

• All the angles of a rectangle are right angles.
• Diagonals of a rectangle are equal and bisect each other

• \[\angle CYA={{40}^{o}}\] is a rectangle \[AC=CY\]

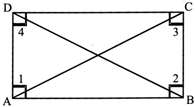
                           \[\therefore \]

\[\angle CYA=\angle CYA={{40}^{o}}\] and \[\angle AXB={{30}^{o}}\]

\[AB=XB\] and \[\therefore \]

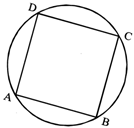
Diagonals AC and BD bisect each other.

 

SQUARE

A rectangle with a pair of adjacent sides equal is a square.

Properties of Square

• All the ratio of a square are equal
• Each of the angles is a right angle in square.
• The diagonals of a square are of equal length.
• The diagonals of a square bisect each other at right angle.

 

CIRCLES

A circle is a simple closed curve, all the points of which are at the same distance from a given fixed point.

 

PARTS OF ACIRCLE

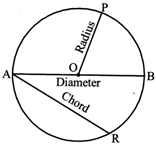
Centre: The fixed point in the plane which is equidistant from every point on the boundary of the circle is called centre. In the adjoining figure, 0 is the centre of the circle.

Radius: The fixed distance between the centre and any point of the circle is called radius. In figure, \[\angle AXB=\angle XAB={{30}^{o}}\] is a radius.

Chord: A line segment joining any two points on a circle is called a chord of the circle. In figure. \[\angle XAY={{180}^{o}}-({{40}^{o}}+{{30}^{o}})={{110}^{o}}\] is a chord.

Diameter: A chord that passes through the centre of a circle is called diameter of the circle. In figure, AB is a diameter. The length of a diameter \[\because \]radius. In a circle, diameter is the longest chord.

Circumference: The distance around a circle is called the circumference. Circumference of a circle is the perimeter of that circle.

Arc: Apart of a circumference is called an arc. In the above figure, the curve line AR is an arc of the circle. It is written as AR.

 

Properties of Circle

• In a circle perpendicular drawn from the centre to a chord bisects the chord.
• If M is the mid-point of \[\Delta ={{180}^{o}}\]\[\angle XAY=\angle XAB+\angle BAC+\angle CAY\].
• In a circle; if a line joining mid-point of a chord to the centre is perpendicular to the chord.

 

• If \[{{110}^{o}}-{{30}^{o}}+\angle BAC+{{40}^{o}}\]\[{{110}^{o}}-{{70}^{o}}=\angle BAC\] \[\Rightarrow \].
• Equal chords of a circle are equidistant from the centre.
• Chords equidistant from the centre are equal in length.

.

If \[\angle BAC={{40}^{o}}.\] \[AN\bot BC\]  \[DE:BC=3:5\]

If \[\frac{AM}{AN}=\frac{3}{5}(Also)\]\[\Delta ADE=\frac{1}{2}(DE)(AM)=\frac{1}{2}(3)(3)=9/2\]\[\Delta ABC=\frac{1}{2}(BC)(AN)=\frac{1}{2}(5)(5)=\frac{25}{2}\]

• Equal chords of a circle subtend equal angles at the centre.
• Chords of a circle which subtend equal angles at the centre are equal.

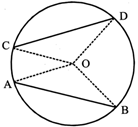
If  \[\Delta ABC-Area\]\[\Delta ADE=\frac{25}{2}-\frac{9}{2}=\frac{16}{2}\] \[\therefore \]

If  \[{{40}^{o}}\]\[{{60}^{o}}\] \[{{90}^{o}}\]

• Angle subtended by an arc at the centre is double the angle subtended by it on the remaining part of the circle.

\[{{30}^{o}}\]

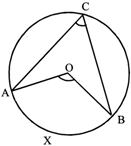
 Angle subtended by the arc AB at the centre is \[{{45}^{o}}\] and the angle subtended by the same arc to the remaining part of the circle is \[{{60}^{o}}\] .

• A quadrilateral is called cyclic if all the four vertices lie on a circle. And the four vertices are called the concyclic points.

·                     

• Sum of opposite internal angles of a cyclic quadrilateral is \[{{75}^{o}}\].

\[\angle CAD={{50}^{o}}\]is a cyclic quadrilateral

                \[\angle BED={{120}^{o}}\] \[\angle BCD\] and \[{{75}^{o}}\]

• Angle made in semi-circle is equal to \[{{105}^{o}}\]

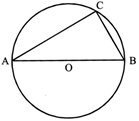
\[{{85}^{o}}\]\[{{60}^{o}}\] is angle of semicircle.

\[\angle BAC={{45}^{o}}\] \[\angle BED={{120}^{o}}\]\[\angle ABD\]

• Angles in the same segment of a circle are equal. Arc AB subtends \[ABCD=\frac{1}{2}(AB+D\times CE)\] and \[\angle R={{138}^{o}}\] is the same segment

\[\angle R={{138}^{o}}\]  \[\angle ACB={{65}^{o}}\]