Quadrilaterals
Category : 8th Class
QUADRILATERALS
FUNDAMENTAL
Polygons: A simple closed figure made up of line segments only, is known as a polygon.
Type of polygons
e.g.: 
e.g.:
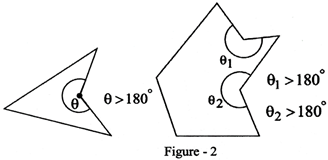
According to another basis, polygons are classified as;
(i) Regular Polygons: Polygons in which all sides and all angles are equal, are called Regular Polygons. Specific names are given to each of them depending upon no of sides.
(a) In Triangles:
Equilateral \[\Delta \,1e\]
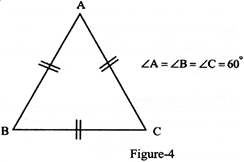
(b) In quadrilaterals: Square
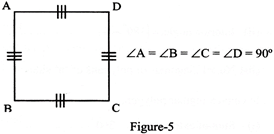
(c) In Pentagons: Regular pentagon
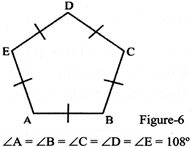
(d) In Hexagons: Regular hexagon
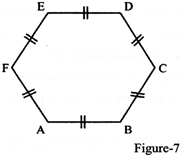
\[\angle A=\angle B=\angle C=\angle D=\angle E=\angle F={{120}^{{}^\circ }}\]& so on.
(ii) Irregular polygons: Polygons which do not nave equal sides or equal angles, are called Irregular Polygons.
Thus, RHOMBUS, which has equal sides but unequal angles, is irregular polygon.
Properties of Regular polygons:-
If n = no. of sides of a regular polygon, then,
(i) Exterior angle, \['\theta '=\left( \frac{{{360}^{{}^\circ }}}{n} \right)\]
(ii) Interior angle, = \[\left( {{180}^{{}^\circ }}-\theta \right)\]
(iii) No. of diagonals of polygons of 'n’ sides \[=\frac{n(n-2)}{2}\]
(i) Sum of exterior \[{{\angle }^{1e}}s={{360}^{{}^\circ }}\]
(ii) Sum of interior \[{{\angle }^{1e}}s=\left( \frac{n-2}{2} \right)*{{360}^{{}^\circ }}\]
Now, we shall concentrate our studies on quadrilaterals.
Quadrilaterals: On the basis of our knowledge of polygons, quadrilaterals are simple closed figures made up of four line segments. Another way to define quadrilateral is as follows:
Quadrilateral
Let, A, B, C, D be four points in a plane. Let 3 or more points be not collinear. The figure formed by four line segments joining points A, B, C and D is called the quadrilateral ABCD.
For Example, look at the quadrilateral ABCD,
(i) the four points A, B, C, D are called its vertices,
(ii) The four line segments AB, BC, CD, and DA are called its sides,
(iii)\[\angle DAB,\angle ABC,\angle BCD,\]and\[\angle CDA\]are known as its angles
(iv) Line segments AC and BD are known as its diagonals.
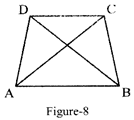
Adjacent sides of a quadrilateral
Sides of a quadrilateral having a common end point are called its adjacent sides. In Figure-8, (AB, BC), (BC, CD), (CD., DA) and (DA, AB) are four pairs of adjacent- sides of quad. ABCD.
Opposite sides of a quadrilateral
Two sides of a quadrilateral are known as its opposite sides if they do have a common end point. In the given figure 8, (AB, DC) and (AD, BC) are two pairs of opposite sides of quad. ABCD.
Adjacent Angles of a Quadrilateral
Two angles of a quadrilateral having common arm are called its adjacent angles. In figure 8, (ZA, ZB), (ZB, ZC), (ZC, ZD) and (ZD, ZA) are four pairs of adjacent angles of quad. ABCD.
Opposite Angles of a Quadrilateral
Non-adjacent angles are known as opposite angles. In figure-8, \[\left( \angle A,\angle C \right)\], and \[\left( \angle B,\angle D \right)\] are two pairs of opposite angles.
Angle Sum property of a Quadrilateral Idea / Thinking behind proof:
Draw a quadrilateral ABCD, draw any diagonal which will divide ABCD into two
\[\Delta \]les ABC and ACD. Use angle sum property in both these \[\Delta \]les.
To prove that: The sum of the angles of a quadrilateral is \[360{}^\circ \]
Proof: Let ABCD be a quadrilateral. Join AC.
Construction: Join diagonal AC. Let \[\angle CAD=\angle 1\And \angle CAB=\angle 2\]
Now, \[\angle 1+\angle 2=\angle A\] ...(i)
Also, \[\angle 3+\angle 4=\angle C\] ...(ii)
\[\therefore \]the sum of the angles of a triangle is = \[{{180}^{{}^\circ }}.\]
\[\therefore \] In \[\Delta ABC,\]
\[\angle 2+\angle 4+\angle B={{180}^{{}^\circ }}.\] ........(iii)

In \[\Delta \]ACD,
\[\angle \text{1}+\angle 3+\angle D={{180}^{{}^\circ }}.\] .....(iv)
Adding (iii) & (iv) we get, \[\angle 2+\angle 4+\angle B+\angle 1+\angle 3+\angle D={{360}^{{}^\circ }}\]
\[\Rightarrow (\angle 1+\angle 2)+\angle B+(\angle 3+\angle 4)+\angle D={{360}^{{}^\circ }}\]
\[\therefore \angle A+\angle \mathbf{B}+\angle C+\angle \mathbf{D}=\mathbf{36}{{\mathbf{0}}^{{}^\circ }}\]
Hence, the sum of the angles of a quadrilateral is \[{{360}^{{}^\circ }}.\]
Special Types of Quadrilaterals
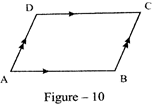
Parallelogram: A quadrilateral is called a parallelogram if both pairs of its opposite sides are parallel. In figure-10, ABCD is a parallelogram \[\left( \parallel grn \right)\]
\[AB\parallel DC\,and\,AD\parallel BC.\]
Rhombus: A parallelogram \[\left( \parallel gm \right)\] having all sides equal is called a rhombus. ABCD is a rhombus in figure-11
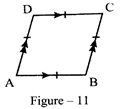
By property of \[\parallel gm,AB\parallel DC;AD\parallel BC\]
By property of rhombus, AB = BC = CD = DA
Rectangle: A parallelogram in which each angle is a right angle is a rectangle.
Figure-12, ABCD is a quadrilateral in which
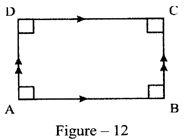
\[AB\parallel DC,AD\parallel BC\] and\[\angle A=\angle B=\angle C=\angle D={{90}^{{}^\circ }}.\]
Note: However, in ABCD, if we do not write\[AB\parallel DC\And AD\parallel BC\], and we simply write \[\angle A=\angle B=\angle C=\angle D={{90}^{{}^\circ }}\], then also it will be a rectangle (because by property of interior \[\angle les,\angle A+\angle B={{180}^{{}^\circ }}\Rightarrow AB\] is transversal on \[AD\And BC\Rightarrow AD\parallel BC)\]
Square: It is a parallelogram in which all me sides are equal and each angle measures 90. In the figure-13,
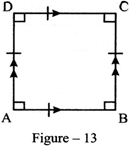
\[AB\parallel DC,AD\parallel BC,AB=BC=CD\] and \[\angle A=\angle B=\angle C=\angle D={{90}^{{}^\circ }}.\]
Although, it looks like a rhombus (because we have drawn it like that), ABCD is a square. In fact, square is a special case of rhombus in which \[\angle A=B=C=D={{90}^{{}^\circ }}\]
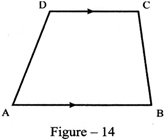
Trapezium: is a quadrilateral having exactly one pair of parallel sides in figure-14, \[AB\parallel DC\]
Isosceles Trapezium: It is trapezium in which non parallel sides are equal. In figure-15,
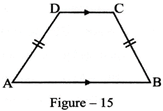
\[AD=BC\Rightarrow ABCD\] is an isosceles trapezium.
Thus, ABCD will be an isosceles trapezium if \[AB\parallel DC\,and\,AD=BC.\]
Kite: It is a quadrilateral in which two pairs of adjacent sides are equal but opposite sides are unequal.

See figure-16, which is self-explanatory, ABCD is a kite.
Key Properties of Quadrilateral with Proofs:
Property 1
In a parallelogram, \[(\parallel gm),\]
(a) Opposite sides are equal (b) Opposite \[\angle les\] are equal (iii) diagonals bisect each other
The converse of the above result can also be used:
(i) A quadrilateral is a \[\parallel gm\] if opposite sides are equal
(ii) A quadrilateral is a \[\parallel gm\]if opposite \[\angle les\] are equal
(iii) A quadrilateral is a \[\parallel gm\]if diagonals bisect each other.
PROOF: Let ABCD be a parallelogram
Construction: Draw diagonal AC.
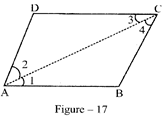
In A ABC and A CDA, We get,
\[\angle 1=\angle 3\] (alternate angles)
\[\angle 2=\angle 4\] (alternate angles)
And \[AC=CA\] (common side)
\[\therefore \] by ASA congruence,
\[\therefore \Delta ABC\cong \Delta CDA\]
\[\Rightarrow AB=CD,BC=DA\] and \[\angle B=\angle D.\] (see the nomenclature, we are not writing AB = DC or \[BC=AD)\Rightarrow \] (a) proved
Similarly, by constructing the diagonal BD, we get
\[\Delta ABD\cong \Delta CDB.\] \[\therefore \angle A=\angle C\]
Thus, (b) proved,
In order to prove (c) consider parallelogram ABCD and draw diagonals AC and BD, intersecting each other at O.
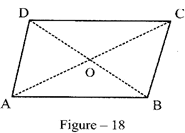
In \[\Delta OAB\] and \[\Delta OCD,\]
\[\angle OAB=\angle OCD\] (alternate angles)
\[\angle AOB=\angle COD\] (vertically opposite angles)
\[AB=CD\] (opposite sides of a parallelogram) By ASA congruence,
\[\therefore \Delta OAB\cong OCD\]
\[\therefore OA=OC\] and \[OB=OD\Rightarrow O\] is the midpoint of AC as well as BD.
Thus, diagonals of a parallelogram bisect each other.
Homework: Prove the three converse results, namely, (i), (ii), & (iii)
Remarks: As discussed earlier, a rectangle, a square and a rhombus are special types of parallelograms. So all the properties of a parallelogram apply to all of them.
Property 2
The diagonals of a rhombus are orthogonal and bisect each other,
PROOF: In figure - 19, ABCD is a rhombus whose diagonals intersect at the point O.
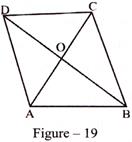
We know that the diagonals of a parallelogram bisect each other.
Every rhombus is a parallelogram.
\[\therefore \]By property of \[\parallel gm,\] diagonals bisect each other.
\[\therefore \] \[OA=OC\] and \[OB=OD\]
Now, the other part of proof is to prove that they are orthogonal, i.e. they intersect at right angles.
From \[{{\Delta }^{1e}}AOB\] and \[{{\Delta }^{1e}}AOD,\]we have:
\[AO=AO\] (common side)
\[AB=AD\] (Sides of a rhombus)
\[OB=OD\] (already proved)
\[\therefore \Delta AOB\cong \Delta AOD\] (by SSS congruence)
\[\Rightarrow \angle AOB=\angle AOD.\]
But, \[\angle AOB+\angle AOD=2\] linear pair of \[{{\angle }^{1e}}s\]
\[\therefore \angle AOB=\angle AOD=\]right angle\[=90{}^\circ \]
Hence, the diagonals of a rhombus are also orthogonal.
Property 3
The diagonals of a rectangle are equal and bisect each other.
PROOF: Let ABCD be a rectangle (figure - 20) whose diagonals AC and BD intersect at the point O.
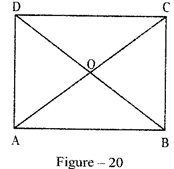
Consider \[{{\Delta }^{les}}ABC\And ABD\] on same base AB
Form \[\Delta ABC\text{ }and\text{ }\Delta BAD\], We have
\[\angle ABC=\angle BAD\] (each equal to\[{{90}^{{}^\circ }}\])
\[AB=BA\] (common side)
BC = AD (opposite sides of a rectangle).
\[\therefore \]By SAS congruence,
\[\therefore ABC\cong \Delta BAD\] \[\Rightarrow AC=BD.\]
Hence, the diagonals of a rectangle are equal. As regards bisection, this has already been proved for \[\parallel gm.\]
Hence, the diagonals of a rectangle are equal and bisect each other.
Property 4
The diagonals of a square are equal, orthogonal (at\[\mathbf{90}{}^\circ \]) and bisect each other.
PROOF: A square is both (a) rectangle and (b) a rhombus.
(a) By property of rectangle, diagonals of square are equal & bisect each other.
(b) By property of rhombus, diagonals of square are orthogonal & bisect each other.
Combing (a) & (b) diagonal of square are (i) orthogonal (ii) equal & (iii) bisect.
Note 1. If the diagonals of a quadrilateral are equal, then it is not necessarily a rectangle.
Note 2. If the diagonals of a quadrilateral intersect at right angles, then it is not necessarily a rhombus.
Homework:
Suitably think of and construct quadrilaterals according to note 1 and note 2 and show it to your teacher.
You need to login to perform this action.
You will be redirected in
3 sec
