8th Class Mathematics Squares and Square Roots Square and Square Roots

SQUARE & SQUARE ROOTS

FUNDAMENTALS

Square and Square Root

• Square: If a number is multiplied by itself, the product so obtained is called the square of that number.
• For a given number x, the square of x is\[\left( x\times x \right)\], denoted by\[{{x}^{2}}\].

e.g., \[{{\left( 4 \right)}^{2}}=4\times 4=16,{{\left( 5 \right)}^{2}}=5\times 5=25,{{\left( 12 \right)}^{2}}=12\times 12=144\]

Perfect squares or Square number;"

• A perfect square is a number that can be expressed as the product of two equal integers.
• It is always expressible as the product of equal factors.

e.g., \[144=2\times 2\times 2\times 2\times 3\times 3={{4}^{2}}\times {{3}^{2}}={{(12)}^{2}}\]

\[81=3\times 3\times 3\times 3={{3}^{2}}\times {{3}^{2}}={{\left( 9 \right)}^{2}}\]

Example:- Show that 300 is not a perfect square.

Solution:- Resolving 300 into prime factors, we get \[300=2\times 2\times 5\times 5\times 3\]

Making pairs of equal factors, we find that the digit 3 is not forming a pair (i.e. it appears only once). Hence 300 is not a perfect square.

Properties of perfect squares

• A number ending in 2, 3, 7 or 8 is never a perfect square

e.g., 82, 73, 177, 2888 etc.

• A number ending in an odd number of zeros is never a perfect square.

e.g., 160, 4000, 900000 end in one zero, three zero, five zeros. So, none of them is a perfect square.

• The square of a even number is always even.

e.g., \[{{2}^{2}}=4,{{8}^{2}}=64,{{10}^{2}}=100,{{20}^{2}}=576\]etc.

• The square of an odd number is always odd.

e.g., \[{{(1)}^{2}}=1,{{(9)}^{2}}=81,{{(27)}^{2}}=729\]etc.

• The square of a proper fraction is smaller than the fraction.

e.g., \[{{\left( \frac{2}{3} \right)}^{2}}=\frac{4}{9}\] and \[\frac{4}{9}<\frac{2}{3}\] since \[4\times 3<9\times 2.\]

• For every natural number n, we have

e.g., \[{{\left( n+1 \right)}^{2}}-{{n}^{2}}=\left( n+1+n \right)\left( n+1-n \right)\]

\[=\left\{ \left( n+1 \right)+n \right\}\]

\[\left\{ {{\left( 36 \right)}^{2}}-{{\left( 35 \right)}^{2}} \right\}=\left( 36+35 \right)\left( 36-35 \right)=71\]

\[\left\{ {{\left( 89 \right)}^{2}}-{{\left( 88 \right)}^{2}} \right\}=\left( 89+88 \right)\left( 89-88 \right)=177\]

• For every natural n, we have sum of the first n odd natural numbers \[={{n}^{2}}\]

e.g.,    (i) \[1+3+5+7+9={{\left( 5 \right)}^{2}}=25\]

(ii) \[1+3+5+7+9+11+13={{\left( 7 \right)}^{2}}=49\]

• Between two consecutive square numbers n² and\[{{(n+1)}^{2}}\], there are 2n non-perfect square numbers.

e.g., Let n = 1         n+1 = 2

            (1)²,               (2)²

2, 3 lie between (1)² and (2)²

\[\Rightarrow \]2n = 2 non-perfect squares numbers between (1)² and (2)²

Pythagorean Triplets 

A triplet (m, n, p) of three natural number, (m, n and p) is called a Pythagoras triplet if \[{{m}^{2}}+{{n}^{2}}={{p}^{2}}.\]

e.g., \[\left( 3,4,5 \right),\left( 5,12,13 \right),\left( 8,15,17 \right)\]etc. are examples of Pythagoras triplets.

Some Shortcuts to find squares

Column Method:- This method is based upon an old Indian method of multiplying two numbers. It is convenient for finding squares of two digit numbers only. This method uses the identity \[{{(x+y)}^{2}}={{x}^{2}}+2xy+{{y}^{2}}\]

e.g., \[{{(52)}^{2}}=\]Let unit place 2 = y and tens place 5 = x

Then follow this Rule

Square root:-

The square root of a number y is that number which when multiplied by itself given y as the product. We denote the square root of a number y by\[\sqrt{y}\].

• In\[\sqrt{y}\], y is called radicand.

Method to find the square root of a number. 

There are two methods:

• Prime factorization method.
• Long-division method.
• Square root of perfect square by the prime factorization method.

Follow these steps.

• Resolve the given number into its prime factors
• Make pairs of equal factors.
• Take the product of the prime factors, choosing one factor out of every pair.

e.g., (1)    Find the square root of 576.

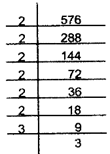
Solution:- By prime factorization, we get

\[576=2\times 2\times 2\times 2\times 2\times 2\times 3\times 3\]

\[\therefore 576=2\times 2\times 2\times 3=24\]

(2) In an auditorium of Global Pratibha School, the number of rows is equal to the number of chairs in each row. If the capacity of auditorium is 5625, find the number of chairs in each row.

Solution:- Let the number of chairs in each row be x.

Then, the number of rows = x

\[\therefore \]Total number of chairs \[=x\times x={{x}^{2}}\]

\[\therefore \]The capacity = 5625

\[\therefore {{x}^{2}}=5625=5\times 5\times 5\times 5\times 5\times 3\times 3\]

\[\therefore \mathbf{x}=5\times 5\times 3\]

            \[\therefore x=75\]

Hence number of chairs in each row = 75.

Square root of the perfect square by the long Division Method

Follow these Steps:-

• Group the digit in pairs, starting with the digit in the unit place. Each pair and the remaining digit in the units place (if any) is called a period.
• Think of the largest number whose square is equal to or just less than the first period.

Take this number as the divisor and also as the quotients

• Subtract the product of the divisor and the quotient from the first period and bring down the next period of the right to the remainder. This becomes new dividend.
• Now the new divisor obtained by taking row times the quotient and annexing with a suitable digit of the quotient, chosen in such a way that the product of the new divisor and this digit is equal to or just less than the new dividend.
• Repeat step 2, 3 and 4 till all periods have been considered.

Example-1:- Evaluate \[\sqrt{15876}\]using long division method.

Solution:- Making periods and using the long division method, we have

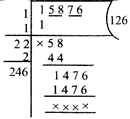
\[\therefore \sqrt{15876}=126\]

Example-2:- What least number must be added to 5607 to make the sum a perfect square? Find this perfect square and its square roots.

Solution:- Try to find out the square root of 5607.

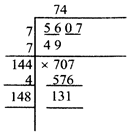
We observe that

\[{{\left( 74 \right)}^{2}}<5607<{{\left( 75 \right)}^{2}}\]

So, required number to be added

\[{{75}^{2}}-5607=5625-5607=18\]

So, 18 should be added and perfect square = 5625.

Square roots of Number in decimal form 

Method makes the number of decimal places even by affixing a zero, if necessary. Now, mark periods and find out the square root by the long division method. Put the decimal point in the square roots as soon as the integral part is exhausted.

Example-3:- Evaluate \[\sqrt{56.25}\]

Solution: -

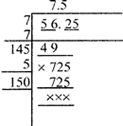
\[\therefore \sqrt{56.25}=7.5\]

Note:-

• Square root of Negative number is not possible.
• For any positive number x any y, we have

(i) \[\sqrt{xy}=\left( \sqrt{x}\times \sqrt{y} \right)\] (ii) \[\sqrt{\frac{x}{y}}=\frac{\sqrt{x}}{\sqrt{y}}\]