8th Class Mental Ability Analytical Reasoning Analytical Reasoning

In this chapter, problems are based upon number of lines, triangles, quadrilaterals etc.

·         To count number of lines, add all number of the horizontal, vertical and slanting lines.

·         To count the number of triangles, add all the number of triangles made up of 1 component, 2 components, 3 components and so on.

·         The same process is for counting the number of other polygons.

Special Case:

Suppose a large square is divided into some small equal squares.

If each side of the big square is sticking 'n' small squares, then the number of all possible squares is obtained by the following formula.

Number of squares = \[{{n}^{2}}+\,\,{{\left( n\text{ }-\text{ }1 \right)}^{2}}+\,\,{{\left( n\text{ }-\text{ }2 \right)}^{2}}+........+\text{ }{{2}^{2}}+\text{ }{{1}^{2}}\]

Note: Number of all squares on a chessboard = 204.

Fig.: Chessboard

EXAMPLE

Count the number of parallelograms in the given figure.

(a) 15                            (b) 12   

(c) 10                            (d) 9

Explanation (a):

The figure may be labelled as shown in the adjoining figure.

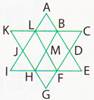
The parallelograms composed of one component each are LMHJ and BDFM i.e., 2 in number.

The parallelograms composed of two components each are ABML and HGFM i.e., 2 in number.

The parallelograms composed of three components each are LBHI, LBEF, BDGH, DFLA, BCFH, KLFH, ABHJ and LFGJ i.e., 8 in number.

The parallelograms composed of six components each are LCFI, KBEH and ADGJ i.e., 3 in number.

\[\therefore \]Total number of parallelograms =2+2+8+3=15.

So the correct option is (a).