Algebra and Co-ordinate Geometry
Category : 9th Class
Algebra and Co-ordinate Geometry
In this chapter, we will learn about polynomials, linear equations in two variables and co-ordinate geometry.
Polynomials
Polynomials are those algebraic expressions in which the variables involved have only non-negative integral powers. In other words, a polynomials p(x) in one variable x is an algebraic expression in x of the form,
\[P(x)={{a}_{n}}{{x}^{n}}+{{a}_{^{n-1}}}{{x}^{n-1}}+....+{{a}_{3}}{{x}^{3}}+{{a}_{2}}{{x}^{2}}+{{a}_{1}}x+{{a}_{0}}.\]
Where \[{{a}_{n}},{{a}_{n-1}},....{{a}_{3}}, {{a}_{2}}, {{a}_{1}}, {{a}_{0}}\]are constants and an \[{{a}_{n}}\ne 0\]
Here, \[{{a}_{n}}, {{a}_{n-1}},...., {{a}_{3}}, {{a}_{2}}, {{a}_{1}}, {{a}_{0}} \]are respectively the coefficients of \[{{x}^{_{n}}}, {{x}^{_{n-1}}}, ...., {{x}^{3}}, {{x}^{2}}, x, {{x}^{0}}\] and n is called the degree of the polynomial.
Each of \[{{a}_{n}}{{x}^{n}}, {{a}_{n-1}}{{x}^{n-1}},.....{{a}_{3}}{{x}^{3}}, {{a}_{2}}{{x}^{2}}, ax, {{a}_{0}}\]is called a term of the polynomial p(x). The degree of the polynomial in one variable is the highest index of the variable in that polynomial.
Note:
(i) A non-zero constant polynomial is a polynomial is a polynomial of degree 0. For example \[-3, \frac{2}{3}, \sqrt{5}\] etc. are constant polynomials.
(ii) Constant polynomial 0 is called the zero polynomial. In such a polynomial all the constants are zero so degree of a zero polynomial is not defined.
(iii) For a polynomial p(x), a real number k is called a root (a zero) of the equation p(x) = 0 p(k) =0.
Types of Polynomials
The following are the types of polynomials:
Remainder Theorem:
If p(x) is a polynomials of degree greater than or equal to 1 and p(x) is divided by the linear polynomial\[x-r\], then the remainder so obtained is p(x).
Factor Theorem:
i. If \[p(r)=0\Rightarrow (x-r)\] is a factor of \[p(x)\]
ii. If \[(x-r)\]is a factor of \[p(x)\Rightarrow p(r)=0\]
Algebraic identities:
Linear Equation in Two Variables
An equation is a statement in which one expression equals to another expression. An equation of the form\[ax+by+c=0,\]where a, b and c real numbers, such that a and b are both non-zero, is called a linear equation in two variables. .
Solution of a Linear Equation in two Variables
A linear equation in two variables has infinitely many solutions.
The solution of a linear equation is not affected on
(i) Adding (or subtracting) the same number in both sides of the equation.
(ii) Multiplying (or dividing) the same non-zero number in both sides of the equation.
Graph of a Linear Equation in Two Variables
General form of liner equation two variables is ax \[ax+by+c=0\]
\[\Rightarrow by=-ax-c\text{ }\Rightarrow \text{y=}\left( \frac{-a}{b} \right)x-\frac{c}{b}\]
The following steps are followed to draw a graph:
Step 1: Express x in terms of y o y in terms of x.
Step 2: Select at least three values of y or x and find the corresponding values of x or y respectively, which satisfies the given equation, write these values of x and y in the form of a table.
Step 3: Plot ordered pair (x, y) from the table on a graph paper.
Step 4: Join these points by a straight line.
Thus we see that the graph formed by every linear equation in two variables is a straight line and every point on the graph (straight line) shows a solution of the linear equation. Also every solution of the linear equation can be represented by a unique point on the graph of the equation.
Note:
(i) The equation of x-axis is \[y=0\] and the equation y-axis is \[x=0\]
(ii) The graph of \[x=k\] is a straight line parallel to the y-axis
(iii) The graph of \[y=k\] is a straight line parallel to the x-axis.
(iv) An equation of the type \[y=kx\] represents a line passing through the origin.
Conditions of Consistency
For a pair of linear equation in two variables:
\[{{a}_{1}}x + {{b}_{1}}y + {{c}_{1}} = 0, {{a}_{2}}x + {{b}_{2}}y + {{c}_{2}} = 0\]
Co-ordinate Geometry
It is the branch of Mathematics in which we solve geometrical problems with the help of algebra. To solve such types of problems we need a Cartesian co-ordinate system.
Cartesian Coordinate System
Two perpendicular lines are required for locating a point in a plane, one of them is horizontal and other is vertical. The horizontal and vertical lines are called x-axis and y-axis respectively.
Suppose X'OX and Y'OY be two mutually perpendicular lines through any point 'O'. The point O is known as origin. Taking a convenient unit of length and starting from the origin mark off a number scale on horizontal as well as on vertical line. The line X'OX is known as X-axis and the line Y'OY is known as Y-axis. Two axis taken together are known as coordinate axis. The coordinates of a point are always written in ordered pair.
Note:
(i) Co-ordinates of a point on x-axis are of the form (x, 0) and that of the point on the y-axis is of the form (0, y)
(ii) If \[x\ne y\], then the position of (x, y) in the Cartesian plane is different from the position of (y, x).
(iii) If \[x\ne y\], then\[\left( x,\text{ }y \right)\ne (y,\text{ x})\]
Quadrants
Let X'ON and Y'OY are the coordinates axes and it divides the given plane into four regions. Every region is known as quadrants.
Signs Convention of a Point Quadrant
|
Sign |
Quadrants |
|
\[(+,+)\] |
I |
|
\[(-,+)\] |
II |
|
\[(-,-)\] |
III |
|
\[(+,-)\] |
IV |
Here, '+' refers to positive real number and '-' refers to negative real number for the coordinates of a point\[\left( x,\text{ }y \right)\].
Distance Formula
If \[A({{x}_{1}},\text{ }{{\text{y}}_{\text{1}}})\] and \[\text{B(}{{\text{x}}_{\text{2}}}\text{, }{{\text{y}}_{\text{2}}}\text{)}\] are the two points in the coordinate system, then the distance AB is given by \[AB=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}}\]
In various geometrical problems we need to use distance formula. Before using this formula the following points must we keep in your mind:
Section Formula
Let the coordinates of end points of a line segment be \[({{x}_{1}},{{y}_{1}})\] and \[({{x}_{2}},{{y}_{2}})\], then the coordinates of point C \[(x,\text{ y})\] which divides the line segment in the ratio m: n internally are:
\[x=\frac{m{{x}_{2}}+n{{x}_{1}}}{m+n}\], \[y=\frac{m{{y}_{2}}+n{{y}_{1}}}{m+n}\]
Note:
(i) If point is the mid-point of AB, then the coordinates of C are: \[\left( \frac{{{x}_{1}}+{{x}_{2}}}{2},\frac{{{y}_{1}}+{{y}_{2}}}{2} \right)\]
(ii) If\[A({{x}_{1}}, {{y}_{1}})\], \[B({{x}_{2}}, {{y}_{2}})\]and \[C({{x}_{3}}, {{y}_{3}})\] are the three vertices of a triangle then its centroid G is given by:
\[\left( \frac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\frac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right)\]
Find the remainder when \[\mathbf{2}{{\mathbf{y}}^{\mathbf{3}}}\mathbf{-3}{{\mathbf{y}}^{\mathbf{2}}}\mathbf{-y+7}\]is divided by \[\mathbf{y-4}\].
(a) 83 (b) 135
(c) 36 (d) \[-\]83
(e) None of these
Ans. (A)
Write the quadrants of the following points in which they lie.
(a) \[(1, 2)\] (b) \[(0, 2)\]
(c) \[(-\,5, -2)\] (d) \[(5, -2)\]
Solution:
(a) \[(1, 2)\] , Here, \[x>0\]and \[y>0\], therefore, it lies in I quadrant.
(b) \[(0, 2)\], Here, \[x=0\] and \[y>0\], therefore it lies on Y- axis.
(c) \[(-\,5, -2)\], Here \[x<0\]and \[y<0\], therefore it lies in IV quadrant.
(d) \[(5, -2)\], Here \[x>0\]and \[y<0\], therefore it lies in IV quadrant.
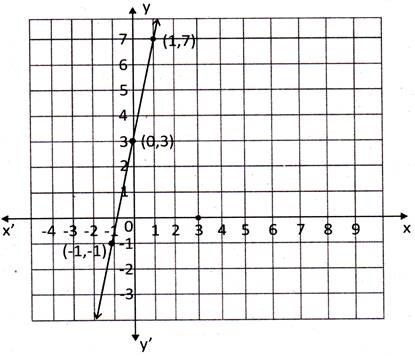
Draw the graph of\[4x-y+3=0\].
Solution:
Step 1: Here it is easy to write y in terms of \[x\Rightarrow y=4x+3\]
Step 2: \[y=4x+3\], if \[x=0\Rightarrow y=3\],
If, \[x=1\Rightarrow y=7\]and if \[x=-1\Rightarrow y=-1\]
|
X |
0 |
1 |
\[-\]1 |
|
Y |
3 |
7 |
\[-\]1 |
Steps 3
Find the value of \[\mathbf{3}{{\mathbf{9}}^{\mathbf{3}}}\mathbf{-2}{{\mathbf{6}}^{\mathbf{3}}}\mathbf{-1}{{\mathbf{3}}^{\mathbf{3}}}\]
Solution: We know that \[{{a}^{3}}+{{b}^{3}}+{{c}^{3}}-3abc=(a+b+c)({{a}^{2}}+{{b}^{2}}+{{c}^{2}}-ab-bc-ca)\]
Or, \[{{a}^{3}}+{{b}^{3}}+{{c}^{3}}=3abc\] {when a + b + c = 0}
Here, a = 39, b = \[-\]26 and c = \[-\]13
\[\Rightarrow a+b+c=39+(-\,26)+(-\,13)=39-39=0\]
\[\therefore 3{{9}^{3}}-2{{6}^{3}}-1{{3}^{3}}=3 \times 39 \times (-\,26) \times (-13) = 39546\]
Example:
Find the square root of \[{{\mathbf{x}}^{\mathbf{4}}}\mathbf{+10}{{\mathbf{x}}^{\mathbf{3}}}\mathbf{+37}{{\mathbf{x}}^{\mathbf{2}}}\mathbf{+60x+36}\]
Solution: The degree of the given polynomial is 4, so its square root will be an expression of degree 2
Let \[a{{x}^{2}}+bx+c\] is the square root of the given expression.
We already know that, \[{{(p+q+r)}^{2}}={{p}^{2}}+{{q}^{2}}+{{r}^{2}}+2pq+2qr+2rp\]
\[\therefore {{(a{{x}^{2}}+bx+c)}^{2}}= {{a}^{2}}{{x}^{4}} + {{b}^{2}}{{x}^{2}} + {{c}^{2}} + 2ab{{x}^{3}} + 2bcx + 2ca{{x}^{2}}\]
\[={{a}^{2}}{{x}^{4}}\text{ }+\text{ }2ab{{x}^{3}}\text{ }+\text{ }({{b}^{2}}+2ac){{x}^{2}}\text{ }+\text{ }2bcx\text{ }+\text{ }{{c}^{2}}\]
Thus we have,
\[{{x}^{4}}+10{{x}^{3}}+37{{x}^{2}}+60x+36\]
\[={{a}^{2}}{{x}^{4}}\text{ }+\text{ }2ab{{x}^{3}}\text{ }+\text{ }({{b}^{2}}+2ac){{x}^{2}}\text{ }+\text{ }2bcx\text{ }+\text{ }{{c}^{2}}\]
On comparing the like terms on either sides of the equation, we get
\[{{x}^{4}}={{a}^{2}}{{x}^{4}}\Rightarrow {{a}^{2}}=1\Rightarrow a=\pm \,1\]
\[10{{x}^{3}}\text{ }=\text{ }2ab{{x}^{3}}\text{ }\Rightarrow \text{ }2ab\text{ }=\text{ }10\text{ }\Rightarrow \text{ }b\text{ }\underline{+}\text{ }5\]
\[37{{x}^{2}}\text{ }=\text{ }({{b}^{2}}+2ac)\text{ }{{x}^{2}}\text{ }\Rightarrow \text{ }{{\text{b}}^{\text{2}}}\text{ }+\text{ }2ac\text{ }=\text{ }37\]
\[\Rightarrow 2ac=37-{{b}^{2}}=37-25=12\]
\[60x\text{ }=2bcx\text{ }\Rightarrow \text{ }2bc\text{ }=\text{ }60\Rightarrow bc=30\]
\[\Rightarrow \text{ c=}\frac{30}{\underline{+}5}=\underline{+}6\]
\[\sqrt{{{x}^{4}}+10{{x}^{3}}+37{{x}^{2}}+60x+36}=(\underline{+}1)\,{{x}^{2}}+(\underline{+}) 5x \underline{+}\,6\]
\[=\underline{+}{{x}^{2}} \underline{+} 5x \underline{+} 6 = ({{x}^{2}}+5x+6) or (-{{x}^{2}} - 5x - 6)\]
If \[{{\mathbf{x}}^{\mathbf{3}}}\mathbf{+a}{{\mathbf{x}}^{\mathbf{2}}}\mathbf{+bx+6}\] has \[\mathbf{(x-2)}\] as a factor and leaves a remainder 18 when divided by\[\mathbf{(x-4)}\], find the value of\[\sqrt{\mathbf{3}{{\mathbf{a}}^{\mathbf{2}}}\mathbf{+2b}}\].
Solution: Let \[p(x)={{x}^{3}}+a{{x}^{2}}+bx+6\]
Since \[(x-2)\]is a factor of p(x)
\[\therefore \text{ } p(2) = 8 + 4a + 2b + 6 = 0\]
\[\Rightarrow \text{ }4a+2b=-14\] ??? (1)
Also \[p(4)=64 + 16a + 4b + 6 = 18\]
\[\Rightarrow 16a + 4b = 18-70 = -52\]
\[\Rightarrow 4a + b = -13\] ??? (2)
On solving equations (1) and (2), we get \[b = -1 \,and a = -3\]
\[\therefore \sqrt{3{{a}^{2}}+2b}=\sqrt{3x{{(-3)}^{2}}+2x-1}=\sqrt{25}=\underline{+}5\]
'In a fraction, if unity is added to the numerator and 2 is subtracted from the denominator then the number becomes\[\frac{\mathbf{4}}{\mathbf{3}}\].' Find the fraction if its denominator is 2 more than the numerator.
Solution: Let the numerator is x and the denominator is y.
\[\therefore Fraction = \frac{x}{y}\]
Now as per the given condition, \[\frac{x+1}{y-2}=\frac{4}{3}\]
\[\Rightarrow \text{ }3x+3=4y-8\]
\[\Rightarrow 3x-4y=-11\]
\[\Rightarrow \text{ }4y-3x=11 .......(i)\]
Since \[y = x + 2\]
\[\therefore \] putting this value in equation (i), we get
\[4(x+2) - 3x = 11\]
\[4x + 8 - 3x = 11 \Rightarrow \text{ }x = 3, so, y = 3 + 2 = 5\]
\[\therefore \] Required fraction is \[\frac{3}{5}\]
Before 14 years, Rahul?s age was 14 times that of Shubham. After 10 years, Rahul?s age will be twice that of Shubham. Find the present age of Rahul and Shubham.
Solution: Let Rahul?s present age is x years and Shubham?s present age is y years.
Now from first condition,
\[x-14 = 14(y-14)\]
\[\Rightarrow \text{ }x - 14 = 14y - 196\]
\[\Rightarrow \text{ } x - 14y = - 182\] ??? (i)
and from second condition,
\[x+10=2 (y+10)\]
\[\Rightarrow x+10=2y+20)\]
\[\Rightarrow x-2y\text{ }=\text{ }10\] ??? (ii)
Subtracting equation (ii) from (i), we get
\[-\,12y=-\,192 \Rightarrow \text{ }y=16\]
\[\therefore \text{ }x=-\,182+14 \times 16 = -182+224 = 42\]
\[\therefore \] Rahul?s present age is 42 years
and Shubham?s present age is 16 years.
Find the area bounded by the line\[ 3x+2y = 6\]with both of the axis.
Solution: The given linear equation is\[ 3x+2y = 6\]
The graph of this line will cuts the x-axis at (2, 0)
\[\{\therefore \text{ }3x+2y = 6 \Rightarrow 3x + 2 \times 0= 6 \Rightarrow x = 2\}\]
Also, the graph of this equation will cut the y-axis at (0, 3)
\[\{\therefore \text{ }3 \times 0 + 2y= 6\}\]
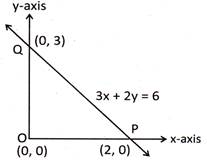
\[\therefore \]The graph of the equation 3x+2y=6 is shown in the figure.
The figure so obtained is of right \[\Delta \]with both the axes.
\[\therefore \] Area of the triangle OPQ is
\[A=\frac{1}{2}\times base \times height\]
\[=\frac{1}{2}\times 2 \times 3 = 3 uni{{t}^{2}}\]
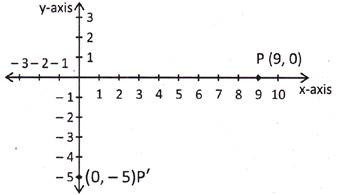
A point lies on the x-axis at a distance of 9 units from the y-axis. What are its coordinates? Find the coordinates if it will lie on y-axis at a distance of 5 units below the x-axis.
Solution: Since, the point is on x ?axis i.e. \[y=0\] and it is at a distance of 9 units from the y-axis so the coordinates of p are \[(9, 0)\]as shown in the graph. Now if it will lie on y-axis i.e. \[(x=0)\]at a distance of 5 units below the x-axis, so the coordinates of it will be (0? -5) and is shown by p? in the shown figure.
Points \[\mathbf{p(6, 0), Q(0, 6)}\]and \[\mathbf{S(0, -6)}\] are three vertices of a square PQRS. Find fourth vertex R and plot it on paper. Also find the area of this square.
Solution: Since, diagonals in a square are equal and here length of QS = 12 units, so length of other diagonal will be 12 units too.
So, coordinates of R are \[(-\,6,\text{ }0)\]
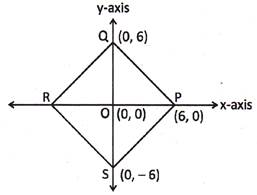
Area of square \[PQRS=2 \times area of \Delta PQR=2 \times \frac{1}{2} \times 12 \times 6\]= 72 sq units
You need to login to perform this action.
You will be redirected in
3 sec
