CIRCLE
FUNDAMENTALS
- Circle:- The collection of all the points in a plane which are equidistant from a fixed point in the plane is called a circle.
- Centre:- The fixed point O is called the centre of the circle.
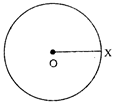
- Radius:- Radius is the distance from centre of a circle in any point on its circumferences Here, OX is a radius.
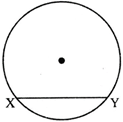
- Chord:- A line segment whose end points on the circumference of a circle is called a chord.
Here, XY is a chord.
- Diameter:- A chord passing through, the centre O of the circle is called a diameter of the circle . It is largest chord of the circle and twice that of the radius.
Here, XY is a diameter.
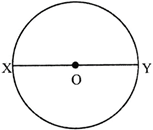
- Semi-circle:- A diameter of a circle divides it into two equal parts and each part is called a semi-circle.
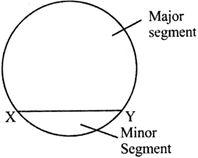
- Segments: A chord divides a circle into two parts,, which are called segments, smaller parts of the circle called minor segment: and larger part is called major segment
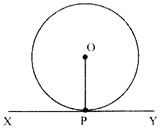
- Tangents:- A line that touches the circle at one end point only is called a tangent.
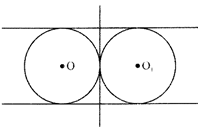
- When two circles touch each other externally, then 3 tangents can be drawn.
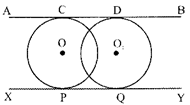
- When two circles intersect each other externally, then two tangents can be drawn.
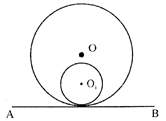
- When one circle touches another circle internally, then only one tangent can be drawn.
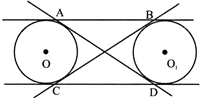
- If two circles do not touches each other then 4 tangents can be drawn.
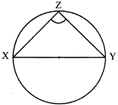
- The angle in a semi - circle is a right angle i.e., \[\angle XZY={{90}^{{}^\circ }}\]
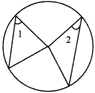
- Angles in the same segment of a circle are equal.
i.e., \[\angle 1=\angle 2\]
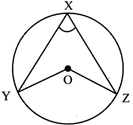
- The angle subtended by an arc of a circle at the centre is twice the angle subtended by it at its circumference.
\[\angle YOZ=2\angle YXZ\]
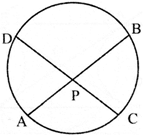
- If AB and CD are chords of circle touch each other at P, then, \[PA\times PB=PC\times PD.\]
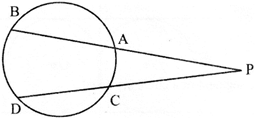
- If chords AB and CD touch each other extremely at P then, \[PA\times PB=PC\times PD\]
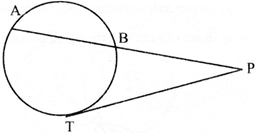
- PT is tangent and AB is a chord. Then \[PA\times PB=P{{T}^{2}}\]

\[xy=\sqrt{{{\left( O{{O}_{1}} \right)}^{2}}-{{\left( {{r}_{1}}-{{r}_{2}} \right)}^{2}}}=\sqrt{4{{r}_{1}}{{r}_{2}}}\]
- Length of transverse tangent

\[AB=\sqrt{{{\left( O{{O}_{1}} \right)}^{2}}-{{\left( {{r}_{1}}+{{r}_{2}} \right)}^{2}}}\]
- Cyclic Quadrilateral:- It is a quadrilateral whose all four vertices lie on the circumrerence of the circle. Also the sum of opposite angle is equal to \[{{180}^{{}^\circ }}\]
i.e., \[\angle A+\angle C={{180}^{{}^\circ }}\]
and \[\angle D+\angle B={{180}^{{}^\circ }}\]



















