9th Class Mathematics Circles Circle

       Introduction

In this chapter we will study about a non-rectilinear figure circle about which we have studied many things in previous classes.  

       Circle

It is a locus of a point which moves in a plane in such a way that its distance from a fixed point is always constant.

We know that the fixed point is called centre and the fixed distance is called its radius \[\text{D}=\text{2r},\text{ C}=\text{2pr}\] Where D is diameter, C is circumference of circle r is radius.  

            Terms Related to Circle

Secant

When a line intersect a circle at two distinct points is called a secant of the circle.

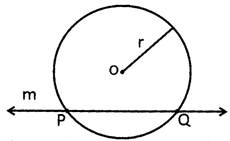
Here, line m is the secant line for circle C(0, r)  

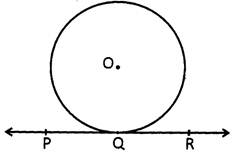
Tangent

A line which touches the circle at exactly one point is called a tangent to the circle. The point at which line touches the circle is called point of contact. Q is said to be point of contact of tangent.

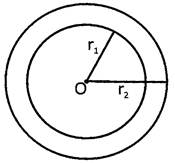
Concentric Circles

Circles are said to be concentric if and only if they have a same centre and different radius.

Arc

A continuous piece of circumference of a circle is called arc.

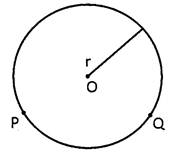
Here, PQ is arc of C(o, r).  

Concurrent Arc

Two arc are said to be concurrent if they subtend same angle at the centre.

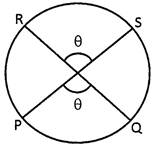
Minor and Major Arcs

If the length of an arc is less then the arc of a semicircle then it is called minor arc and which is greater than the semicircles is called major arc. arc \[\overset\frown{PRQ}\] is minor arc and \[\overset\frown{PSQ}\] is major arc

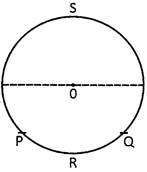
Segment

The region bounded by chord and an arc is called segment. The segment which contains minor arc is called minor segment and which contains major arc is called major segment.

Congruent Circles

Two circles are said to be congruent if they have same radii.  

Important Properties

•   Equal chord of a circle subtends equal angle at the centre.
•   If two arc of a circle are equal then the corresponding chords are equal.
•   The perpendicular from the centre of a circle to a chord bisect the chord.
•   The perpendicular bisector of the two chords of a circle intersect at the center.
•   Equal chords of a circle are equidistant from the centre.