9th Class Mathematics Circles Theorems Related to Tangent of a Circle

       Theorems Related to Tangent of a Circle  

 

Theorem 1

A tangent of a circle is perpendicular to the radius through the point of contact  

Given: I is the tangent to the circle c (o, r) at point A  

To prove: \[OA\bot \ell \]

 

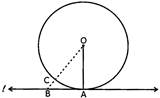
Construction:

Take a point B on line I other than A and join OB. Let OB cut the circle at the point C.  

Proof:

Since O does not lies l. Therefore, the shortest distance from 0 to I will be the perpendicular so it is sufficient to prove OA is the shortest distance.

From figure

\[\text{OA}=\text{OC}\]   \[\Rightarrow \] \[~\text{OA}<\text{PN}\]

OA is the shorter than any other segment joining 0 to any point on I. Hence, \[~\text{OA}\bot \ell \]  

 

Theorem 2

The length of tangent drawn from an external point to a circle are equal.  

Given: PA and PB are the tangents from point P to circle C (o, r).  

To Prove:    PA = PB

Construction:

Join PO, OA and BO  

Proof:

In \[\Delta \text{POA}\] and \[\Delta \text{POB}\]

\[\text{PO}=\text{OP}\]                               (common)

\[\text{OA}=\text{OB}\]                              (radius of circle)

\[\angle \text{OAP}=\angle \text{OBP}=\text{9}0{}^\circ \]

By R.H.S Criteria

\[\Delta \text{POA}\cong \Delta \text{POB}\]

\[\frac{\text{By C}\text{.P}.\text{C}\text{.T}}{\text{PA}=\text{PB}}\]

Hence, proved  

 

Another method:

In\[\Delta \text{POA}\]

\[P{{A}^{2}}+O{{A}^{2}}=P{{O}^{2}}\]                    ...(i)

In \[\Delta \text{POB}\]

\[\text{P}{{\text{B}}^{\text{2}}}+\text{O}{{\text{B}}^{\text{2}}}=\text{P}{{\text{O}}^{\text{2}}}\]                          ...(ii)

From (i) and (ii) we get

\[\text{P}{{\text{A}}^{\text{2}}}+\text{O}{{\text{A}}^{\text{2}}}=\text{P}{{\text{B}}^{\text{2}}}+\text{O}{{\text{B}}^{\text{2}}}\]

\[\Rightarrow \]\[\text{P}{{\text{A}}^{\text{2}}}=\text{P}{{\text{B}}^{\text{2}}}\](Since\[\text{O}{{\text{A}}^{\text{2}}}=\text{O}{{\text{B}}^{\text{2}}}\], because they are radius) \[\Rightarrow \] \[\text{PA}=\text{PB}\]

Hence, proved.    

 

 

 

• The relation between the pair of numbers 220 and 284 is that all the factors of 220 which is less than itself add up to 284 and vice versa,
• Archimedes proved that the area of a circle equals the area of a triangle whose height equals the radius of the circle and whose base equals its circumference,
• \[\text{1}/\text{81}=.0\text{12345679}0\text{12345679}0..\] where 8 is missing and \[1+2+3+4+5+6+7+9\]\[=37\].
• Similarly, \[\text{6}+\text{6}+\text{6}=\text{18}\] and \[\text{18}\times \text{37}=\text{666}\].\[4+4+4=12\] and \[12\times 37=444\]  

 

 

• Circle is a locus of a point which moves in a plane in such a way that its distance from a fixed point is always constant.
• Secant is a line which intersect a circle at two distinct points.
• Tangent is a line which touches the circle at exactly one point.
• Two circles are said to be congruent if they have same radii.
• A tangent of a circle sis perpendicular to the radius through the point of contact.
• The length of tangent drawn from an external points to a circle are equal.            

 

 

 

 

  In an isosceles A PQR in which PQ = QR. A circle which passes through P and R intersect at point L and M to the side PQ and QR respectively as shown in the figure then which one of the following is true?

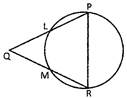
(a) L and M are the mid points of PQ and QR respectively

(b) \[\text{LM}=\frac{1}{2}\text{PR}\]

(c) \[\text{LM}|\,\,|\text{PR}\]                   

(d) \[\angle PQR=\angle QLM\]

(e) None of these  

 

Answer: (c)  

Explanation:

Since, \[\Delta \text{PQR}\] is isosceles triangle in which \[PQ=QR\] \[\Rightarrow \] \[\angle QPR=\angle QRP\]

Since, LMRP is a cyclic quadrilateral

\[\angle \text{LPR}+\angle \text{LMR}=\text{18}0{}^\circ \]                       .... (i)

and \[\angle \text{MLP}+\angle \text{MRP}=\text{18}0{}^\circ \]            ....(ii)

From (i) and (ii), we get \[\angle \text{MLP}=\angle \text{LMR}\]                             ...(iii)

and \[\text{QML}+\text{LMR}=\text{l8}0{}^\circ \]          ....(iv)

From (i) and (iv)

\[\Rightarrow \]\[\angle \text{QML}+\angle \text{LMR}=\angle \text{LPR}+\angle \text{LMR}\]

\[\Rightarrow \] \[\angle \text{QML}=\angle \text{LPR}\] \[\Rightarrow \] \[\angle \text{QML}=\angle \text{QRP}\]                      [because \[\angle \text{LPR}=\angle \text{QRP}\]]

Since, corresponding angles are equal

Therefore, \[LM\,|\,\,|\,\,QR\]  

 

 

  In the figure given below PQ is the diametre of the circle with center O. If PT and QS are the perpendicular to the line I, and QS meet the circle at point R then which one of the following is correct?

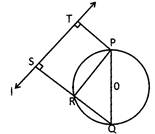
(a) \[\Delta \text{PRT}\] is acute angled triangle   

(b) TP = RS

(c) Quadrilateral RPST is a square  

(d) \[\angle \text{SRP}\] is obtuse angle

(e) None of these

 

Answer: (b)  

 

 

  In the figure given below which one of the following relations is correct?

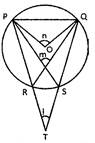
(a) \[\angle m=\angle l+\angle n\]                          

(b) \[\angle l=\angle m-\angle n\]

(c) \[\angle m=\angle n-\angle l\]                           

(d) \[\angle n=\angle m-\angle l\]

(e) None of these

 

Answer: (c)  

 

 

  Find the radius of circle if a chord of length is 30cm which is drawn at a distance of 8 cm from centre of circle.

(a) 17cm                                              

(b) 15cm

(c) 4cm                                                

(d) 12cm

(e) None of these

 

Answer: (a)  

 

 

  In the figure given below AP and AQ are tangents from point A to a circle whose centre is O. Another tangents through M intersects AP and AO at L & N respectively and tangents at y intersects at x and z respectively then which one of the options is correct.

(a) XZ=PX+QZ                                   

(b) LN=LM+PL

(c) AL=AN                                           

(d) XZ=QZ+YZ

(d) None of these

 

Answer: (a)