9th Class Mathematics Coordinate Geometry Centroid and Incenter of a Triangle

        Centroid and Incenter of a Triangle

The coordinate of centroid of a triangle whose vertices are \[({{x}_{1}},{{y}_{1}}),({{x}_{2}},{{y}_{2}})\] and \[({{x}_{3}},{{y}_{3}})\] is \[\left( \frac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\frac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right)\]

The coordinate of the in centre of a triangle ABC whose vertices are \[A({{x}_{1}},{{y}_{1}}),B({{x}_{2}},{{y}_{2}})\] and \[C({{x}_{3}},{{y}_{3}})\] is \[\left( \frac{a{{x}_{1}}+b{{x}_{2}}+c{{x}_{3}}}{a+b+c},\frac{a{{y}_{1}}+b{{y}_{2}}+c{{y}_{3}}}{a+b+c} \right)\]    

• Before Rene Descartes many steps had been taken to correlate geometry and algebra.
• The Greek mathematician Menaechmus proved theorems by using a methods that had resemblance to the use of coordinates and it has sometimes been maintained that he had introduced analytic geometry. Apollonius of perga, in on determinate section, dealt with problems in a manner that may be called and analytic geometry of one dimension; with the question of finding points on a line thatwere in a ration to the others. [Apollonius in the conics further developed thought to have anticipated the work of Descartes by some 1800 years.]  

• Quadrants divide Euclidean plane in four plane region.
• Point lies in the first quadrant if \[x>0,y>0\], in the second quadrant if \[x<0,y>0\] in the fourth quadrant if \[x>0,y<0,\] on X-axis if \[y=0\],on y-axis if \[x=0\].  

  The ratio in which line \[y=x-2\] divides the line segment joining (8, 9) and (3,-1) is_____.

(a) 3:2                                                  

(b) \[\frac{3}{4}:\frac{4}{2}\]

(c) 2:3                                                   

(d) 3:3

(e) None of these  

Answer: (c)  

Explanation:

Given line is \[y=x-2\]                                    ..... (i)

Let P=(8,9) and Q=(3,-1)

let line (i) divides PQ, in the ratio K : 1 at point R;

then \[R=\left( \frac{8k+3}{k+1},\frac{9k-1}{k+1} \right)\]

Since R lies on \[y=x-2\], therefore,

\[\frac{9k-1}{k+1}=\frac{8k+3}{k+1}-2\]

\[\Rightarrow \]\[\frac{9k-1}{k+1}-\frac{8k+3}{k+1}=-2\] \[\Rightarrow \]\[\frac{9k-1-8k-3}{k+1}=-2\]

\[\Rightarrow \]\[\frac{k-4}{k+1}=-2\] \[\Rightarrow \]\[k-4=-2(k+1)\] \[\Rightarrow \]\[k-4=-2k-2\] \[\Rightarrow \]\[3k=4-2\] \[\Rightarrow \]\[k=\frac{2}{3}\]

Then the ratio is k : 1 \[\Rightarrow \]\[\frac{2}{3}:1\]                               \[\Rightarrow \]\[2:3\]  

  Find the coordinate of point which trisect the line segment joining the points (1, 3) and (3, 9).

(a) (5, 5), (3, 3)                                 

(b) (5, 5), (7, 7)

(c) \[\left( \frac{5}{3},5 \right)\left( \frac{7}{3},7 \right)\]                             

(d) \[\left( \frac{5}{3},\frac{7}{3} \right)\left( 5,7 \right)\]               

(e) None of these  

Answer: (c)  

Explanation:

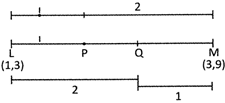
The coordinate of point P is

\[x=\frac{3\times 1+2\times 1}{3}=\frac{5}{3}\]

\[y=\frac{3\times 2+9\times 1}{3}=\frac{{{\bcancel{15}}^{3}}}{3}=5\]  

The coordinate of point Q is

\[x=\frac{1\times 1+3\times 2}{3}=\frac{7}{3}\]

\[y=\frac{3\times 1+9\times 2}{3}=\frac{21}{3}=7\]  

Thus the coordinate of point P is \[\left( \frac{5}{3},5 \right)\] and Q is \[\left( \frac{7}{3},7 \right)\].  

  The coordinate of centroid of a triangle whose vertices are (3, 2), (-3,-1) and (0, -1) is.....

(a) (0, 0)                                              

(b) (0, 3)

(c) (3, 0)                                              

(d) (0,-5)

(e) None of these  

Answer: (a)  

  If the point (m, n) is equilateral from \[(x+y,y-x)\] and \[(x-y,x+y)\] then which one of the following options is true?

(a) \[\frac{x+y}{x-y}=\frac{m+n}{n-m}\]              

(b) \[(m+n)(m-n)=(x+y)(x-y)\]

(c) \[(m+n)(x+y)=(m-n)(x-y)\]

(d) \[\frac{n-m}{n+m}=\frac{x-y}{x+y}\]

(e) None of these  

Answer: (a)