9th Class Mathematics Coordinate Geometry Distance Formula

       Distance Formula

Let the coordinate of two points A and B be \[({{x}_{1}},{{y}_{1}})\] and \[({{x}_{2}},{{y}_{2}})\] respectively then the distance between two points A and B can be found in the following way:

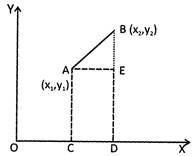
Take points A and B draws AE perpendicular to BD.

Thus \[OC={{x}_{1}},AC={{y}_{1}}\]

\[OD={{x}_{2}},BD={{y}_{2}}\]

Now \[AE={{x}_{2}}-{{x}_{1}}\] and \[BE={{y}_{2}}-{{y}_{1}}\]

In right \[\Delta \text{AEB}\]

\[\text{A}{{\text{B}}^{\text{2}}}~~=\text{A}{{\text{E}}^{\text{2}}}+\text{B}{{\text{E}}^{\text{2}}}\]

\[\Rightarrow \]\[A{{B}^{2}}={{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}\] \[\Rightarrow \]\[AB=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}}\]  

            Important Points to Use Distance Formula

In various geometrical problems in which we need to use distance formula. Before using this formula the following points must keep in your mind:

1.   If \[A=({{x}_{1}}-{{y}_{1}})\]and\[B=({{x}_{2}}-{{y}_{2}})\] then \[AB=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}}\] or \[\sqrt{{{({{x}_{1}}-{{x}_{2}})}^{2}}+{{({{y}_{1}}-{{y}_{1}})}^{2}}}\]

2.   The distance of point \[C(x,y)\] from origin is \[\sqrt{{{x}^{2}}+{{y}^{2}}}\].

3.   To show three points P, Q. and R are collinear find PQ, QR and PR and then show that the greatest of these three is equal to the sum of other two.

4.   Use the following geometrical facts:

(i) A triangle is equilateral if all sides are equal.

(ii) A quadrilateral is parallelogram if opposite sides are equal.

(iii) A quadrilateral is rectangle if opposite sides are equal and diagonals are equal.

(iv) A quadrilateral is rhombus if all four sides are equal.  

The circumcentre of a circle whose vertices are (-1, 0), (7, -6) and (-2, 3) is.... .

(a) (5, 0)                                              

(b) (3, -3)

(c) (-3, 3)                                             

(d) (4, 3)

(e) None of these  

Answer: (b)  

Explanation:

Let the coordinate of circumcentre be \[p(x,y)\] and A = (-1, 0), B = (7, -6) and C = (-2, 3)

Since P is the circumcentre

\[\text{P}{{\text{A}}^{\text{2}}}=\text{P}{{\text{B}}^{\text{2}}}\]

\[\Rightarrow \]\[{{(x+1)}^{2}}+{{y}^{2}}={{(x-7)}^{2}}+{{(y+6)}^{2}}\]

\[\Rightarrow \]\[{{(x+1)}^{2}}-{{(x-7)}^{2}}={{(y+6)}^{2}}-{{y}^{2}}\]

\[\Rightarrow \]\[(x+1+x-7)(\bcancel{y}+1-\bcancel{y}+7)=(y+6+y)(\bcancel{y}+6-\bcancel{y})\]

\[\Rightarrow \]\[(2x-6).8=(2y+6).6\] \[\Rightarrow \]\[4(x-3)=12(y+3)\]

\[\Rightarrow \]\[4x-12=3y+9\] \[\Rightarrow \]\[4x-3y=21\]                                            ...(i)

\[P{{A}^{2}}=P{{C}^{2}}\]

\[\Rightarrow \]\[{{(x+1)}^{2}}+{{y}^{2}}={{(x+2)}^{2}}+{{y}^{2}}\] \[\Rightarrow \]\[4x+6y+13=2x+1\]

\[\Rightarrow \]\[x+3y=-6\]                                                        ...(ii)  

adding (i) and (ii), we get

\[\begin{align}   & 4x-3y=21 \\  & \,\,\underline{x+3y=-6} \\  & \,\,5x\,\,\,\,\,\,\,\,\,\,=15 \\ \end{align}\]

\[x=3\]  

Now put the value of x in (ii), we get               

\[3+3y=-6\]        \[\Rightarrow \]               \[3y=-9\]                 \[y=-3\]

the coordinate of circumcentre is (3, - 3).