9th Class Mathematics Coordinate Geometry Section Formula

       Section Formula

Let the coordinate of end points of a line segment be \[({{x}_{1}},{{y}_{1}})\]and\[({{x}_{2}},{{y}_{2}})\] then the coordinate of point C which divides the line segment in the ratio m : n is:

\[x=\frac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\,\,y=\frac{m{{y}_{2}}+n{{y}_{1}}}{m+n}\]  

Proof:

Let point \[C(x,y)\] be the point which divides the line segment joining two given points  \[A({{x}_{1}},{{y}_{1}})\] and \[B({{x}_{2}},{{y}_{2}})\] internally in the ratio m : n.

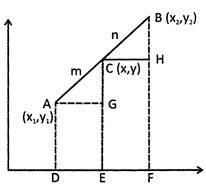
From A, B and C draw AD, BF and CE perpendicular to x - axis.

From A and C draw AG and CH perpendicular to CE and BF.

Then \[AG={{x}_{1}}-{{x}_{1}}\]

\[CH={{x}_{2}}-x\]

\[CG=y-{{y}_{1}}\]

\[BH={{y}_{2}}-y\]

\[\Delta \text{AGC}\] and \[\Delta \text{BCH}\] are similar. Therefore,

\[\frac{AG}{CH}=\frac{CG}{BH}=\frac{AC}{BC}\]

\[\Rightarrow \] \[\frac{x-{{x}_{1}}}{{{x}_{2}}-x}=\frac{y-{{y}_{1}}}{{{y}_{2}}-y}=\frac{m}{n}\] \[\Rightarrow \] \[\frac{x-{{x}_{1}}}{{{x}_{2}}-x}=\frac{m}{n}\] \[\Rightarrow \] \[nx-n{{x}_{1}}=m{{x}_{2}}-mx\] \[\Rightarrow \]

\[(m+n)x=m{{x}_{2}}+n{{x}_{1}}\]                 \[x=\frac{m{{x}_{2}}+n{{x}_{1}}}{m+n}\]

Similarly \[\frac{y-{{y}_{1}}}{{{y}_{2}}-y}=\frac{m}{n}\]    \[\Rightarrow \]                \[y=\frac{m{{y}_{2}}+n{{y}_{1}}}{m+n}\]

Thus the coordinate of point C is\[\left( \frac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\frac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right)\]

Note: If point C is the midpoint of AB then the coordinate of C is \[\left( \frac{{{x}_{1}}+{{x}_{2}}}{2},\frac{{{y}_{1}}+{{y}_{2}}}{2} \right)\]