9th Class Mathematics Geometry

 

Geometry

 

In this chapter, we will learn about introduction to euclid’s geometry, lines and angles, triangles, quadrilaterals, areas of parallelograms and triangles and circles.

 

Axioms

Axioms or postulates are the assumptions which are obvious universal truths. They are not proved.

 

Theorems

Theorems are statements which are proved using definitions, axioms, previously proved statements and deductive reasoning.

 

Euclid’s Axioms

1. The things which are equal to the same thing are equal to one another.
2. If equals be added to the equals, the wholes are equal.
3. If equals be subtracted from equals, the remainders are equals.
4. Things which coincide with one another are equal to one another.
5. The whole is greater than the part.
6. Things which are double of the same thing are equal to one another.
7. Things which are halves of the same thing are equal to one another.

 

Euclid’s Postulates

1. A straight line may be drawn from any point to any other point.
2. A terminated line (line segment) can be produced indefinitely.
3. A circle may be described with any centre and any radius.
4. All right angles are equal to one another.
5. If a straight line falling on two straight lines makes the interior angles on the same side of it, taken together less than two right angles, then the two straight lines if produced indefinitely, meet on that side on which the sum of angles is taken together less than two right angles.

 

Point

A point is a fine dot. For example, P is a point as shown in the figure.

                                    \[\bullet P\]

 

Line Segment

A line segment is a straight path between two given points. For example in the shown figure PQ is a straight path between the pints P and Q and so is called a line segment \[\overline{PQ}\]

A line segment has a definite length.

 

Ray

A ray is a line segment extending indefinitely in one direction. A ray has no definite length. For example, in the shown figure \[\overrightarrow{PQ}\] is representing a ray having one and point P.

Line

A line is a ne is obtained on extending a line segment indefinitely in both the directions. In the shown figure, 0\[\overleftrightarrow{PQ}\] is represented as a line. A line has no end points so a line has no definite lengths.

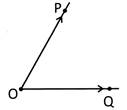
Angle

An angle is generated when two rays originated from the same end point. In the shown figure POQ is the angle formed by two rays  \[\]and \[\]. Here O is called the vertex of the \[\angle \]POQ and PO and OQ are called the arms of the angle POQ.

 

Note:

(i) If a ray stands on a line, then so formed adjacent angles are supplementary and its converse.

(ii) The vertically opposite angles formed by two intersecting lines are equal.

 

Parallel Lines and a Transversal

If a transversal intersects two parallel lines, then

(i) Each pair of alternate interior angles is equal and conversely.

(ii) Each pair of corresponding angles is equal and conversely.

(iii) Each pair of interior angles on the same side of the transversal is supplementary and conversely.

 

Note: Lines parallel to the same line are parallel to each other.

 

Triangle

A closed figure formed by three line segments is called a triangle. A triangle has three sides, three angles and three vertices. Two figures of same shape and same size are called congruent figures. Two circles of the same radii are congruent. Two triangles ABC and PQR are congruent \[(ie.\,\,\Delta \,\,ABC\cong \Delta \,\,PQR)\]under the correspondence \[A\leftrightarrow P,\,\,B\leftrightarrow Q\,\,and\,\,C\leftrightarrow R\]

 

Note:

(i) Sum of all the three interior angles of a triangle is\[180{}^\circ \].

(ii) The exterior angle of a triangle is equal to the sum of the corresponding two interior opposite angles.

 

Congruent Figures

Two geometrical figures are said to be congruent if they have same shape and size. e.g. two angles are said to be congruent if they have same measures similarly two line segments are said to be congruent if they have same lengths.

 

Congruency of Triangles

Two triangles ABC and DEF are said to be congruent if and only if, AB = DE, BC = EF, CA =FD, \[\angle \]A = \[\angle \]D, \[\angle \]B = \[\angle \]E and \[\angle \]C = \[\angle \]F.

 

                    

 

Criteria for Congruency of triangles

There are generally four criteria for the congruency of triangles which are given below.

 

S-S-S Criteria

Two triangles are said to be congruent if the three sides of one triangle are equal to the corresponding three sides of the other.

 

S-A-S Criteria

Two triangles are said to be congruent if the two sides and included angle of one triangle is equal to the other.

 

A-S-A Criteria

If the two angles and the side included by the angles are equal to the corresponding two angles and included side of the other triangle, then the two triangles are congruent.

 

R-H-S Criteria

This criteria is for a right-angled triangle. If one side and hypotenuse of a right-angled triangle is equal to the corresponding side and hypotenuse of other right-angled triangle then two right angled triangles are said to be congruent.

 

Some Important Results

• The longer side of a triangle has greater angle opposite to it.
• The greater angle of a triangle has longer side opposite to it.
• Perpendicular line segment is shortest in length.
• The sum of any two sides of a triangle is greater than the third side.
• The difference between any two sides of a triangle is always less than its third side.
• Angles opposite to equal sides of a triangle are equal.
• Sides opposite to equal angles of a triangle are equal.

 

Similarity of Triangles

When two geometrical shapes resembles same but need not to be equal in size are called similar figures. Let us observe the following examples:

(i) Any two line segments are always similar.

(ii) Two circles of different radius are always similar.

(iii) For rectilinear figures if all the corresponding angles of a polygon are equal and the ratio of their corresponding sides are also equal, then they are said to be similar.

The criteria of similarity of two triangles are

(i)  A-A-A criterion                       (ii) S-S-S criterion

(iii) S-A-S criterion

The ratio of the areas of two similar triangles is equal to the ratio of the,

• Squares of any two sides of the triangles.
• Squares of their altitudes.
• Squares of their corresponding medians.
• Squares of their corresponding angle bisector segments.

 

Quadrilaterals

A Plane figure bounded by four line segments is called a quadrilateral.

 

 

• Points J, K, L and M are the vertices of quadrilateral JKLM.
• The line segments JK, KL, LM and MJ are the sides of the quadrilateral.
• The two sides of a quadrilateral having a common point are called adjacent sides.
• The two sides having no common end points is called opposite side.
• Two angles of a quadrilateral having common arm are called adjacent angles.
• Two angles of a quadrilateral having no common arm are called opposite angles.

 

Properties of a Quadrilateral

• A quadrilateral is a parallelogram, if

      (i) Opposite sides are equal.

Or   (ii) Opposite angles are equal.

Or   (iii) Diagonals bisect each other.

Or   (iv) A pair of opposite sides is equal and parallel.

• In a rectangle, diagonals are equal and bisect each other and vice-versa.
• In a rhombus, diagonals bisect each other at right angles and vice-versa.
• In a square, diagonals bisect each other at right angles and are equal and vice-versa.
• The line segments joining the mid-points of any two sides of a triangle is parallel to a third side and is half of it.
• A line through the mid-point of a side of a triangle parallel to another side bisects the third side.
• The quadrilateral formed by joining the mid-points of the sides of a quadrilateral, in order, is a parallelogram.
• The diagonals of a rectangle are equal.
• If the two diagonals of a parallelogram are equal then the parallelogram is a rectangle.
• The diagonal of a rhombus are perpendicular to each other.
• A parallelogram is a square if the diagonals of a parallelogram are equal and intersect at right angles.
• The sum of all angles of a quadrilateral is always\[360{}^\circ \].

 

Results on Areas of Parallelograms and Triangles

• Any diagonal of a parallelogram divides it into two triangles of equal area.
• Triangles which are on the same base and between the same parallel lines are equal in area.
• A median of a triangle divides it into two triangles of equal areas.
• Area of a triangle is half the product of its base and the corresponding altitude.
• Triangles on the same base and having equal areas lie between the same parallels
• If a parallelogram and a triangle are on the same base and between the same parallels, then area of the triangle is half the area of the parallelogram.
• Area of a parallelogram is the product of its base and the corresponding altitude.
• A parallelogram and a rectangle on the same base and between the same parallels are equal in area.
• Parallelograms which are on the same base and between the same parallel lines are equal in area.

 

Circle

Circle is the locus of a point which moves in a plane in such a way that its distance from a fixed point is always constant. We know that the fixed point is called centre and the fixed distance is called its radius. Also,

 

\[D\text{ }=\text{ }2r\],\[C=2\pi r\], where D is diameter, C is circumference of circle and r is radius.

 

Terms Related to a Circle

Following are some terms which are very useful in solving the problems related to circles.

 

Secant

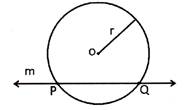
When a line intersects a circle at two distinct points, it is called a secant of the circle. In the following figure line m is a secant of the circle.

 

Tangent

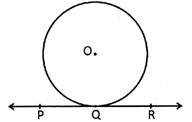
A line which touches the circle at exactly one point is called a tangent to the circle. In the following figure PQR is a tangent of the circle.

 

 

Concentric Circles

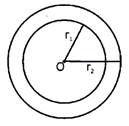
Circles are said to be concentric if and only if they have the same centre and different radii.

 

 

Concurrent Arc

A continuous piece of circumference of a circle is called an arc and two arcs are said to be concurrent if they subtend equal angles at the centre.

 

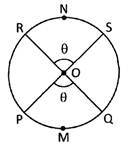
Here, \[Arc\,\,\overset\frown{RNS}\equiv Arc\overset\frown{\,\,PMQ}\]

 

Properties of Circles

• Equal chords of a circle (or of congruent circles) subtend equal angles at the centre.
• If the angles subtended by two chords of a circle (or of congruent circles) at the centre (corresponding centres) are equal, the chords are equal.
• The perpendicular drawn form the centre of a circle to a chord bisects the chord.
• There is only one circle possible which can pass through three non collinear points.
• The line drawn through the centre of a circle to bisect a chord is perpendicular to the
• Equal chords of a circle are equidistant from the centres.
• Chords equidistant from the centre of a circle are equal in length.
• If two chords of a circle are equal, then their corresponding arcs are congruent and its converse.
• The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
• Angles in the same segment of a circle are equal.

 

Note:

(i) The sum of either pair of opposite angles of a cyclic quadrilateral is\[180{}^\circ \].

(ii) If the sum of a pair of opposite angles of a quadrilateral is 180°, the quadrilateral is cyclic.

(iii) Radius of incircle and circumcircle of an equilateral triangle of side a  \[a=\frac{a}{2\sqrt{3}}\]  and \[\frac{a}{\sqrt{3}}\] respectively.

 

Example:

In the figure given below the height of two poles are 10 metres and 15 metres. If the poles are 30 metres apart then the height of point of intersection of the lines joining the top of each pole from opposite foot of the other pole is:

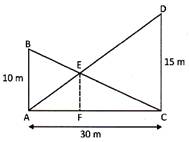
(a) 18m                         (b) 8m              

(c) 6m                           (d) 9 m

(e) None of these

 

Answer (c)

In the given figure, \[\Delta CAB\sim \Delta CEF\Rightarrow \frac{EF}{10}\]\[=\frac{FC}{30}\Rightarrow FC=3EF\]

 

Similarly in \[\Delta ACD\sim \Delta AFE,\] so we have \[\frac{EF}{15}=\frac{AF}{30}\Rightarrow AF=2EF\]

From above equations, we get \[5EF=30\Rightarrow EF=6m\]

 

Example:

In an equilateral triangle show that the centroid and circumcenter coincide.

 

Solution:

 

Given: An equilateral triangle PQR in which M, L and N are the mid points of sides QR, RP and PQ respectively.

To prove: The centroid and circumcentre are coincident in \[\Delta PQR\]

Construction: Draw medians PM, QL and RN

Proof: Let G be the centroid of \[\Delta PQR\] is the point of intersection of medians QL, RN and MP.

In \[\Delta QNR\] and \[\Delta QLR\]we have,

 

 

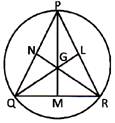
\[\angle Q=\angle R=60{}^\circ \] and QN=RL and QR=RQ

\[\Rightarrow \] (By SAS)

\[\Rightarrow \]RN=QL (CPCT)                     … (i)

     Similarly, in \[\Delta RPN\cong \Delta PRM\]

\[\Rightarrow \]RN = PM (CPCT)                    ... (ii)

From (i) and (ii), we get

     RN = PM = QL

\[\Rightarrow \]\[\frac{2}{3}\] RN \[\frac{2}{3}\] PM = \[\frac{2}{3}\] QL

\[\Rightarrow \] GR= GP = QG \[\Rightarrow \] G is equidistant from the vertices.

\[\Rightarrow \] G is circumcentre of\[\Delta PQR\].

Hence the centroid and circumcentre of \[\Delta PQR\] are coincident.

 

Example:

In the figure given below.

 

 

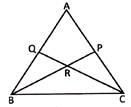
\[\frac{AP}{PC}=\frac{3}{4}\] and \[\frac{BR}{RP}=\frac{3}{2}\] and  BQ = 15 cm. Find AQ

 

Solution:

 

Given: \[\frac{AP}{PC}=\frac{3}{4}\], \[\frac{BR}{RP}=\frac{3}{2}\] and BQ = 15cm

 

 

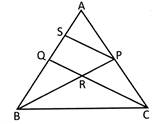
Draw PS || CQ which meets AB at S.

Applying basic proportionality theorem, we get

 

\[\frac{BQ}{QS}=\frac{BR}{RP}\Rightarrow \frac{15}{QS}=\frac{3}{2}\Rightarrow \]QS=10 cm.

 

Similarly in\[\Delta AQC\], we get

\[\frac{AS}{SQ}=\frac{BR}{PC}\Rightarrow\frac{AS}{10}=\frac{3}{2}\Rightarrow AS=\frac{30}{4}\]= 7.5 cm.

\[\therefore \] AQ = AS + QS = 10 + 7.5 = 17.5 cm.