9th Class Mathematics Related to Competitive Exam Formulae

       Formulae  

             Circumference and Area of a Circle

For a circle of radius r, we have

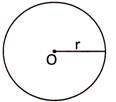
(i) Circumference of the circle \[=2\pi r\]

(ii) Area of the circle \[=\pi {{r}^{2}}\]

(iii) Area of the semicircle \[=\frac{1}{2}\pi {{r}^{2}}\]

(iv) Perimetre of the semicircle \[=\pi r+2r\] 

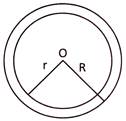
Area of Ring

Let R & r be the outer and inner radii of ring. Here area of the ring \[=\pi ({{R}^{2}}-{{r}^{2}})\]

Length of Arc, Area of Sector and Segment

Let an arc AB makes an angle\[\theta <180{}^\circ \]at the center of a circle of radius r then we have:

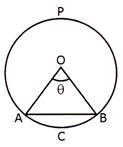
(i) Length of the arc AB\[=\frac{2\pi r\theta }{360}\]

(ii) Area of the sector OACB \[=\frac{\pi {{r}^{2}}\theta }{360}\]

(iii) Perimetre of the sector\[\text{OACB}=\text{OA}+\text{OB}+\]length of\[\overset\frown{AB}+2r+\frac{2\pi \theta }{360}\]

(iv) Area of the minor segment ACBA = (Area of the sector OACB) - (area of\[\Delta OAB\])\[=\left( \frac{\pi {{r}^{2}}\theta }{360}-\frac{1}{2}{{r}^{2}}\sin \theta  \right)\]

(v) Area of the major segment BDAB = (area of the circle) - (area of the minor segment ACBA)  

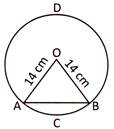
A chord of a circle of radius 14 cm makes a right angle of the centre. Find the area of the major segments of the circle.

(a) \[\text{59}0\,\text{c}{{\text{m}}^{\text{2}}}\]                                           

(b) \[\text{56}0\,\text{c}{{\text{m}}^{\text{2}}}\]      

(c) \[\text{595}\,\text{c}{{\text{m}}^{\text{3}}}\]                                           

(d) \[\text{995}\,\text{c}{{\text{m}}^{\text{2}}}\]

(e) None of these

Answer: (b)  

Explanation

Let AB be the chord of a circle of centre 0 & radius = 14 cm

so that\[\angle \text{AOB}=\text{9}0{}^\circ \]

Area of the sector OACB

\[=\frac{\pi {{r}^{2}}\theta }{360}c{{m}^{2}}=\left( \frac{22}{7}\times 14\times 14\times \frac{90}{360} \right)c{{m}^{2}}=154c{{m}^{2}}\]

Area of \[\Delta \text{OAB}=\frac{1}{2}{{r}^{2}}\sin \theta \]

\[=\left( \frac{1}{2}\times 14\times 14\times \sin 90{}^\circ  \right)=\text{98c}{{\text{m}}^{\text{2}}}=\] Area of the minor segment ACBA

= (area of the sector OACB) - (area of the \[\Delta \text{OAB}\])\[=(\text{154}-\text{98})\text{c}{{\text{m}}^{\text{2}}}=\text{56}\,\text{c}{{\text{m}}^{2}}\] Area of the major segment BDAB

= (area of the circle) - (area of the minor segment)

\[\text{=}\left\{ \left( \frac{22}{2}\times 14\times 14 \right)-56 \right\}\text{c}{{\text{m}}^{\text{2}}}=(\text{616}-\text{56})\text{c}{{\text{m}}^{\text{2}}}=\text{56}0\text{ c}{{\text{m}}^{\text{2}}}\]