10th Class Mathematics Real Numbers Irrational Number

         Irrational Number

The decimal representation of an irrational number is non-terminating and non-repeating. In other words we can say that non-terminating and non-repeating decimals are called irrational numbers.  

(i) 10.0202002000200002................

(ii) The square of any positive integer which is not a perfect square is irrational are irrational number

(iii) is an irrational number  

              Properties of Irrational Numbers  

1.    The sum of two irrational numbers may or may not be irrational.  

(i) Suppose , then , which is irrational

(ii) Suppose two irrational numbers and  then which is not irrational.  

2.    The difference of two rational numbers may or may not be irrational  

(i) then  which is irrational

(ii) Suppose, then , which is not an irrational number

3.    The product of two irrational numbers may or may not be irrational. For example the product ofand 5 = 44, which is a rational number.

4.    The quotient of two irrational numbers may or may not be irrational. For example, which is not irrational.

5.    The sum of an irrational number and a rational number is irrational.

6.    The difference of an irrational number and a rational number is irrational.

7.    The product of an irrational number and a rational number may or may not be irrational.

8.    The quotient of an irrational number and a rational number is irrational.  

            Representation of Irrational Numbers on Number Lines

Suppose x' ox be a horizontal line and let 0 be the origin. Take OP as 1 unit and draw so that PQ = 1 unit with centre 0 and OQ as radius draw an arc; meeting at A. Then OA = OQ =unit (by Pythagoras theorem)

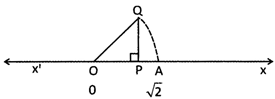
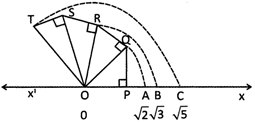
Similarly diagrams given below shows