9th Class Mathematics Surface Areas and Volumes Surface Area and Volume

Surface Area and Volume

In this chapter, we will learn about some important formulas related to 2-D and 3-D geometrical shapes.

Area of a Triangle

•           Area of a triangle \[=\frac{1}{2}\times (Perpendicular)\times Base\]
•          Area of a triangle having lengths of the sides a, b and c is \[=\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}\]sq. units, where \[s=\frac{1}{2}(a+b+c)\]

•           Area of an equilateral triangle\[=\frac{\sqrt{3}}{4}{{a}^{2}}\], where a is the side of the equilateral triangle.

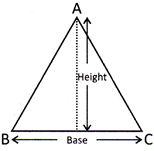
Circle                        

•           Circumference of the circle = \[2\pi r\]
•           Area of the circle =\[\pi {{r}^{2}}\]
•           Area of the semicircle = \[\frac{1}{2}\pi {{r}^{2}}\]
•           Perimeter of the semicircle \[=\pi r+2r\]

Length of Arc and Area of a Sector

Let an arc AB an angle 0 < 180° at the center (O) of a circle a4 radius; Then we have:

•            Length of the arc \[AB=\frac{2\pi \theta }{360{}^\circ }\]
•            Area of the sector \[OACB=\frac{\pi {{r}^{2}}\theta }{360{}^\circ }\]

•            Area of the minor segments ACBA = area of sector OACB \[-\] of the corresponding triangle AOB
•            Area of the major segment ADBA = area of the circle-area of the minor segment

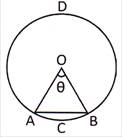
Perimeter and Area of a Rectangle

Let ABCD be a rectangle in which length \[AB\text{ }=1\] units, breadth \[BC\text{ }=\text{ }b\] units then we have:

•           \[Area\text{ }=\text{ }\left( l\text{ }\times \text{ }b \right)\text{ }square\text{ }units\]
•           \[Length\text{ }\left( l \right)=\frac{area\text{ (A)}}{breadth\text{ (B)}}units\]

•           \[breadth\text{ }\left( b \right)\text{ }=\text{ }\frac{area\text{ (A)}}{length\text{ (l)}}units\]
•           Diagonal (d) \[=\sqrt{{{l}^{2}}+{{b}^{2}}}\text{ }units\]
•           Perimeter \[\left( p \right)\text{ }=\text{ }2\left( l\text{ }+\text{ }b \right)\] units

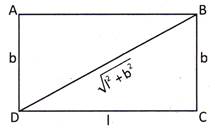
Area of Four Walls of a Room

Let I, b and h are respectively the length/ breadth and height of a room, then area of four walls of the room =\[\left\{ 2\,\left( l+b \right)\times h \right\}\text{ }sq\text{ }units.\]

Perimeter and Area of Square

Let ABCD be a square with each side equal to ?a? units, then

•            Area = a2 sq. units
•           \[Area={{\left( \frac{1}{2}\times {{(diagonal)}^{2}} \right)}^{{}}}sq.\text{ }units\]

•             \[Diagonal\text{ =a}\sqrt{2}\text{ units}\]
•            Perimeter = 4a units

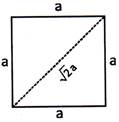
Area of Some Special Types of Quadrilateral

•           Area of a parallelogram = (base \[\times \] height)

•           Area of a rhombus \[=\frac{1}{2}\times (product\text{ of  diagonal})\]

•           Area of a Trapezium \[=\frac{1}{2}\](Sum of length of parallel sides) \[\times \](distance between then)\[=\frac{1}{2}(a+b)\times h\]

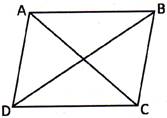
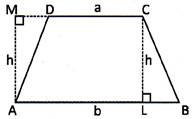
Solids

The objects having definite shape and size are called solids. A solid occupies a definite space.

Cuboid

For a cuboid of length = l, breadth = b and height = h, we have:

•            Volume = \[\left( l\times b\times h \right)\]cubic units
•           Total surface area = \[2\left( lb + bh + lh \right)\] sq. units
•            Lateral surface area \[=~\left[ 2\left( l\text{ }+\text{ }b \right)\text{ }x\text{ }h \right]\text{ }sq.\text{ }units\]
•           Diagonal of a cuboid = \[\sqrt{{{l}^{2}}+{{b}^{2}}+{{h}^{2}}}\]

        Cube

For a cube having each edge = a units, we have:

•            Volume = a3 cubic units
•           Total surface area = 6a2 sq. units
•           Lateral surface area = 4a2 sq. units
•           Diagonal of a cube = \[a\text{ }\sqrt{3}\]

Cylinder

Solids like jar, circular pencils, circular pipes, road rollers, gas cylinders are of cylindrical shape. For a cylinder of base radius = r units and height = h units, we have:

•           Volume = \[\pi {{r}^{2}}h\] cubic units
•           Curved surface area = \[2\pi rh\] square units
•          Total surface area = \[(2\pi rh+2\pi {{r}^{2}})=\text{ }2\pi r(h+r)\text{ }sq.\text{ }units\]

Cone

Consider a cone in which base radius = r, height = h and slant height\[\left( l \right)=\sqrt{{{h}^{2}}+{{r}^{2}}}\], then we have:

•            Volume of the cone \[\frac{1}{3}\pi {{r}^{2}}h\]
•           Curved surface area of the cone = \[\pi rl\]
•        Total surface area of the cone\[~=\left( curved\text{ }surface\text{ }area \right)+\left( area\text{ }of\text{ }the\text{ }base \right)=\pi rl+\pi {{r}^{2}}=\pi r\left( l+r \right)\]

Sphere

Objects like a football, a cricket ball, etc. are of spherical shapes. For a sphere of radius r, we have:

•           Volume of the sphere \[=\frac{4}{3}\pi {{r}^{3}}\]
•           Surface area of the sphere =\[4\pi {{r}^{3}}\]

Hemisphere

A plane through the centre of a sphere cuts it into two equal parts, each part is called a hemisphere. For a hemisphere of radius r, we have:

•           Volume of the hemisphere =\[\frac{2}{3}\pi {{r}^{3}}\]
•           Curved surface area of the hemisphere = \[2\pi {{r}^{2}}\]
•          Total surface area of the hemisphere = \[~3\pi {{r}^{2}}\]

•             Example:

Find the area of the triangle whose base is 25 cm and height is 10.8 cm.

            (a) 125 \[c{{m}^{2}}\]                                                             (b) 135 \[c{{m}^{2}}\]

            (c) 124 \[c{{m}^{2}}\]                                                              (d) 199 \[c{{m}^{2}}\]

            (e) None of these

Ans.     (b)

Explanation: Area of the given triangle \[=\left( \frac{1}{2}\times 25\times \text{10}\text{.8} \right)c{{m}^{2}}=135\text{ }c{{m}^{2}}\]

•             Example:

A chord of a circle of radius 14 cm makes a right angle at the centre. Find the area of the major sector of the circle.

            (a) 590\[c{{m}^{2}}\]                                                 (b) 462\[c{{m}^{2}}\]

            (c) 595\[c{{m}^{2}}\]                                                               (d) 995\[c{{m}^{2}}\]

            (e) None of these

Ans.     (b)

Explanation: Area of the major sector \[\frac{270}{360{}^\circ }\times \pi {{r}^{2}}\]

            = \[\frac{270{}^\circ }{360{}^\circ }\times \frac{22}{7}\times 14\times 14=462\text{ c}{{\text{m}}^{\text{2}}}\]

•            Example:

The length of a rectangular plot of land is twice its breadth. If the perimeter of the plot is 210 m, then find its area.

            (a) 2450\[{{m}^{2}}\]                                                              (b) 2251\[{{m}^{2}}\]

            (c) 5560\[{{m}^{2}}\]                                                              (d) 9060\[{{m}^{2}}\]

            (e) None of these

Ans.     (a)

Explanation: Let x metre be the breadth of the triangle, then its length will be 2x metre.

Now, \[2(x+2x)=210\Rightarrow \text{ }x=35\]

\[Area=35\times 70=2450\text{ }{{m}^{2}}\]