9th Class Mathematics Surface Areas and Volumes

Surface Areas and Volumes

• Cuboid: Let be the length, V the breadth and 'h' the height of a cuboid, then

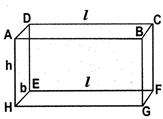
            (i) Sum of the lengths of the 12 edges of a cuboid                                                

            (ii) Lateral surface area \[=2\left( l+b \right)\times h\]

            (iii) Total surface area \[=2\left( lb\text{  }bh\text{ }+\text{ }hl \right)\]    

            (iv) Diagonal  \[=\sqrt{{{l}^{2}}+{{b}^{2}}+{{h}^{2}}}\]                        

            (v) Volume

• Cube: If 'a' is the edge of a cube, then

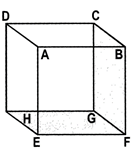
            (i) Sum of the lengths of the 12 edges of a cube = 12a               

            (ii) Lateral surface area \[=\text{ }4{{a}^{2}}\]

            (iii) Total surface area \[=\text{ }6{{a}^{2}}\]

            (iv) Diagonal \[=\sqrt{3}\]

            (v) Volume\[=\text{ }{{a}^{3}}\]

• Cylinder: If 'r' is the radius and 'h' is the height of a cylinder, then

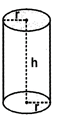
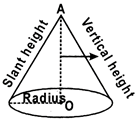
            (i) Curved or lateral surface area \[=2\pi rh\]

            (ii) Total surface area \[=\text{ }2\pi r\left( h+r \right)\]

            (iii) Volume\[=\pi {{r}^{2}}h\]                                                         
                                                   

• Hollow cylinder: A solid bounded by two co-axial cylinders of the same height but with different radii is called a hollow cylinder.

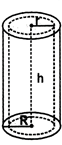
            If 'r' is the radius of the inner cylinder 'R' is the radius of the outer cylinder and 'h' is the height of the hollow cylinder then

            (i) Curved or lateral surface area\[=2\pi r\left( R+r \right)h\]

            (ii) Total surface area\[=\text{ }2\pi \left( R+r \right)\left( h+R-r \right)\]

            (iii) Volume \[=\pi h\left( {{R}^{2}}-{{r}^{2}} \right)\]

• Cone: If \['l'\]is the slant height,\['r'\] is the radius of the base and 'h' is the vertical height of a cone, then                 
• Curved surface area\[=\pi rl\]
• Total surface area \[=\pi r\left( l+r \right)\] (iii) Volume =\[\frac{1}{3}\pi {{r}^{2}}h\]                                                                                       
• Slant height, \[l=\sqrt{{{h}^{2}}+{{r}^{2}}}\]

• Sphere: A sphere is a solid which can be defined as the set of all points in space which are equidistant from a fixed point, If 'r' is the radius of a sphere, then

            (i) Surface area \[4\pi {{r}^{2}}\]sq. units                          

            (ii) Volume \[=\frac{4}{3}{{T}^{3}}\]cu. units

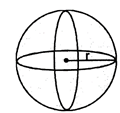
Note: L.S.A and TSA are the same for a sphere.        

• Hemisphere: A plane passing through the centre of a sphere divides the sphere into two equal parts, each of which is called a hemisphere.

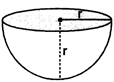
            If 'r' is the radius of the sphere from which a hemisphere is cut out, then

            (i) Curved surface area \[=2\pi {{r}^{2}}\]sq. units

            (ii) Total surface area \[=\text{ }3\pi r2\]sq. units

            (iii) Volume \[=\frac{2}{3}\pi {{r}^{3}}\]cu. units.